深海采矿系统悬链线立管动力响应分析1)
2020-10-28郐艳荣魏明珠周济福
郐艳荣 魏明珠† 王 旭 周济福†,
∗(中国科学院力学研究所流固耦合系统力学重点实验室,北京100190)
†(中国科学院大学工程科学学院,北京100049)
深海采矿系统由水面船、自航浮体、海底集矿机、输送站及提升矿石的立管(包括悬链线立管、垂直硬管、浮力软管) 组成[1],如图1(a) 所示,因长径比很大,立管在水动力作用下柔性效应显著。柔性立管在海洋中受到海流、波浪及水面船运动等的影响[2],其动力响应影响着立管的安全稳定,是人们热切关注的重要问题之一。准确计算柔性立管的动力响应,分析不同因素的影响规律,对深海工程设计具有重要意义。
深海采矿系统悬链线立管顶部与水面船相连,水面船在海洋环境下的运动对立管产生的影响是动力分析中需要考虑的关键因素。对此国内外学者进行了大量的研究[3-4],表明水面船的拖航速度越大,立管的水平位移越大[5],而水面船运动位移和周期对立管的动力响应均可产生显著影响[6],且有研究表明立管的水平位移增幅可达水面船运动位移幅值[7]。因此,立管顶部水面船的运动可增加立管在动载荷作用下的偏移,引起立管失稳[8],但水面船的运动对立管动力特性的影响规律尚不明确。
海流作为海洋立管经受的主要载荷,对立管的动力特性影响显著,很多学者对此进行了不同程度的研究[9-10],但研究对象多为结构形式简单的竖直立管[7]。悬链线立管几何外形更复杂,海流诱导的流场作用下悬链线立管的动力响应计算变得更加困难。此外,也有研究考虑了多因素共同作用下立管的动力响应问题[11-12],但较少同时考虑海流作用和水面船运动影响下悬链线立管的动力响应。
本文基于有限元模型,针对深海采矿系统悬链线立管,如图1(b),所遭遇海流、水面船运动特性,研究悬链线立管在海流和水面船运动共同影响下的动力响应,包括水面船运动位移幅值、周期对立管等效应力和位移的影响。
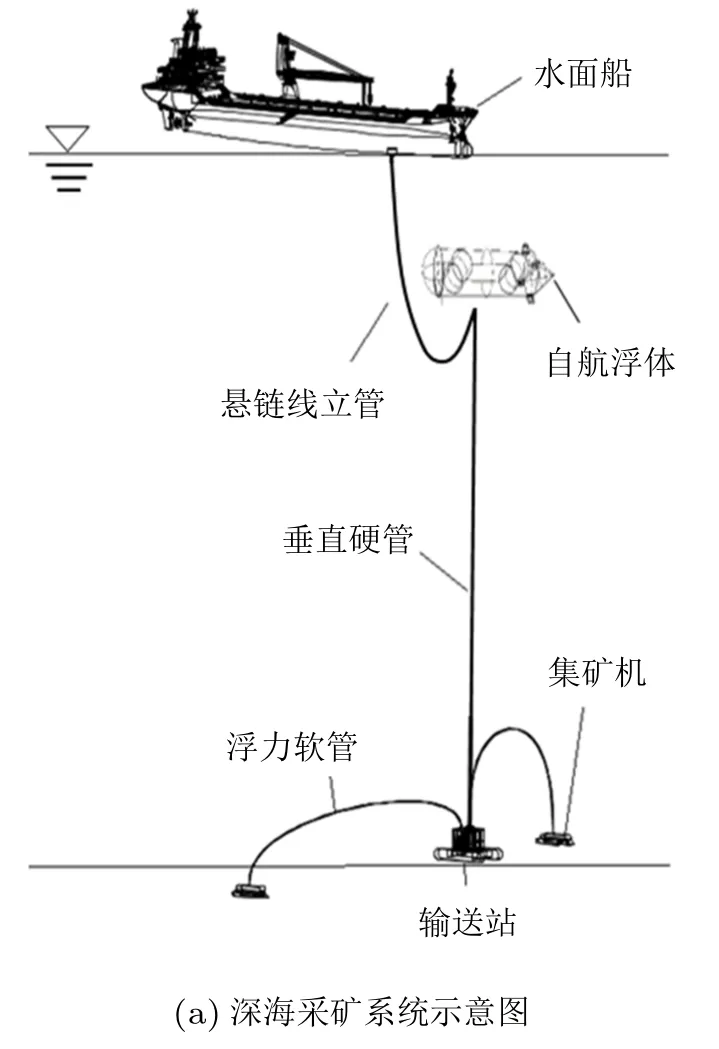
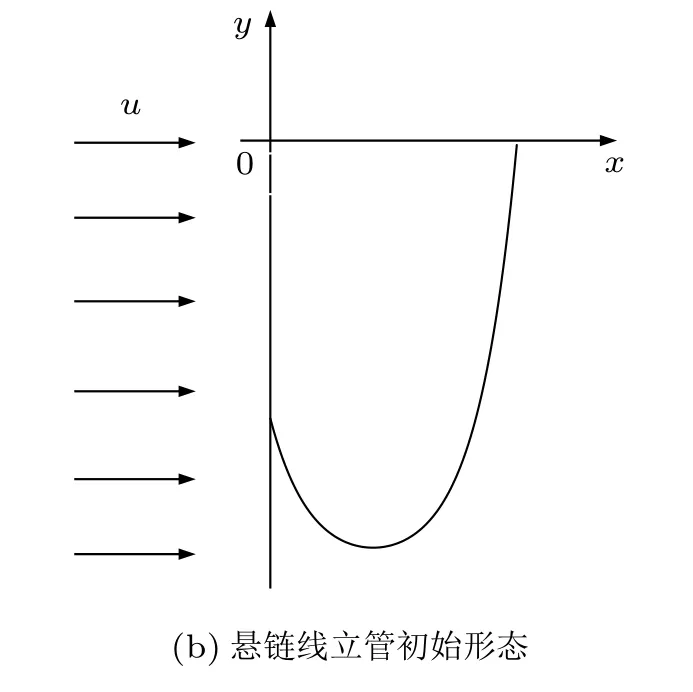
图1 深海采矿系统和悬链线立管初始形态
1 数学模型
1.1 控制方程
本文采用如下形式的结构运动控制方程

式中,M为质量矩阵;K为刚度矩阵;F为外载荷,如流体载荷;X为结构位移;为结构运动速度;为结构运动加速度。采用有限元方法计算,隐式Newmark 法求解式(1)。
采用莫里森公式计算流体载荷[13],则流体载荷F由两部分组成,一是由流场的速度u引起的黏性阻力FD,也称为拖曳力;二是由流场的加速度∂u/∂t引起的惯性力FI。同时考虑结构运动的影响,则单位长度结构所受海流载荷的计算公式为
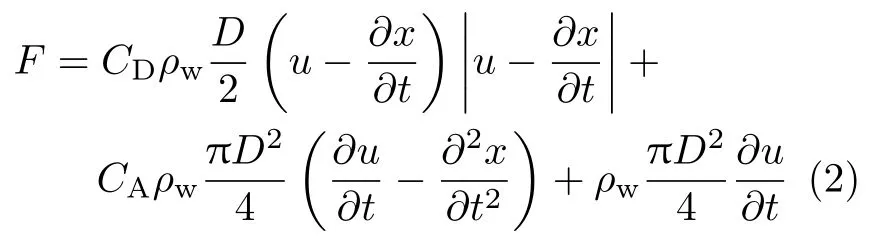
式中,ρw为海水密度,取值1022 kg/m3;u为垂直于结构的海流流速;CD和CM分别为拖曳力系数和惯性力系数。CA为附加质量力系数,满足CM=CA+1;∂x/∂t和∂2x/∂t2分别为结构的运动速度和加速度。
1.2 边界条件
为了便于研究,将位于悬链线立管顶部水面船的运动简化为竖直平面内(即xy平面)的椭圆运动。因此,悬链线立管顶部采用随水面船运动的铰接。悬链线立管的另一端连接自航浮体,自航浮体具有自动定位功能,保持静止状态,因此,与立管连接处采用固定铰接。
1.3 模型验证
文献[14] 计算了顶张力立管在墨西哥湾定常剪切流下的运动响应。本文采用相同的流速、顶张力立管参数、水动力系数及边界条件进行有限元模型验证,具体参数见文献[14],得到沿立管轴向的等效应力和位移分布,并与文献[14] 的结果进行对比,如图2 所示。图2(a) 表明,在顶张力和海流共同作用下,立管的等效应力沿轴线方向的分布规律与文献[14] 的计算结果一致。图2(b) 说明,本文计算得到的立管的位移分布情况基本与文献[14] 的计算结果一致。
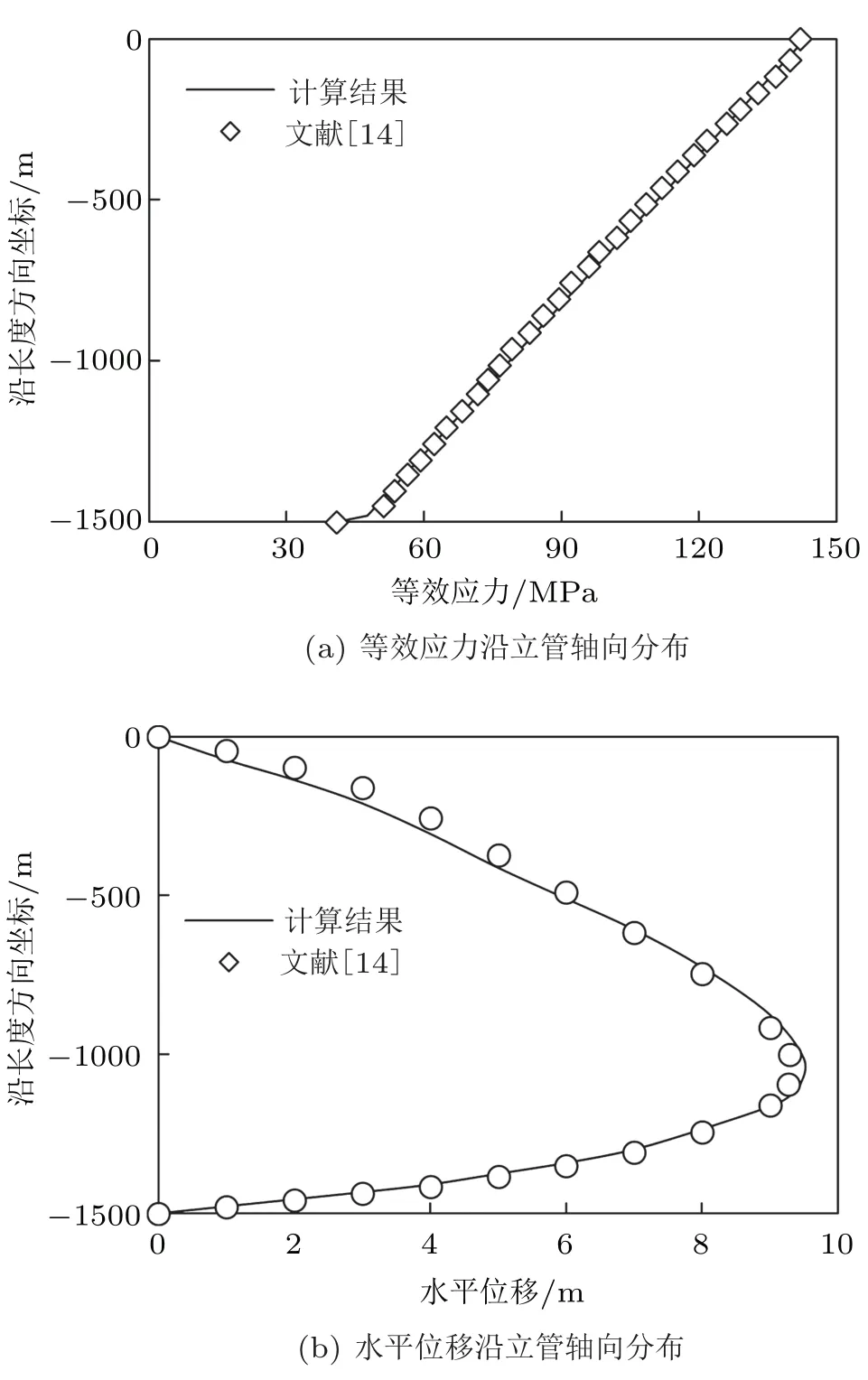
图2 计算结果与文献结果对比
2 结果分析
2.1 材料属性及计算工况
悬链线立管在海水中受重力和浮力作用处于静止状态时,根据其总长和两端点之间的相对位置,可得到悬链线立管的初始形态。本文中采用的悬链线立管总长为400 m,两端点垂向间距为200 m[1],水平间距为100 m。计算中采用计及立管截面属性的线模型,并考虑海流方向与悬链线立管所在铅直面(xy平面) 平行的情况,如图1(b) 所示。本文主要关注悬链线立管的强度问题,即在流体拖曳力作用下悬链线立管产生的大位移和应力问题,所以未考虑涡激振动的影响,因而是一个二维问题,故单元类型采用二维二阶梁单元,并将模型离散为400 个单元。
悬链线立管物理参数如表1 所示。其中,E为立管的弹性模量,G为立管的剪切模量,ρs为立管的密度,D为立管的外径,d为立管的内径,L为立管的总长。

表1 悬链线立管参数
本文主要关注水面船运动特性对悬链线立管动力特性的影响,具体计算条件及参数取值列于表2,共包括11 组算例。其中,u为海流流速,H为水面船运动位移幅值,T为水面船运动周期。
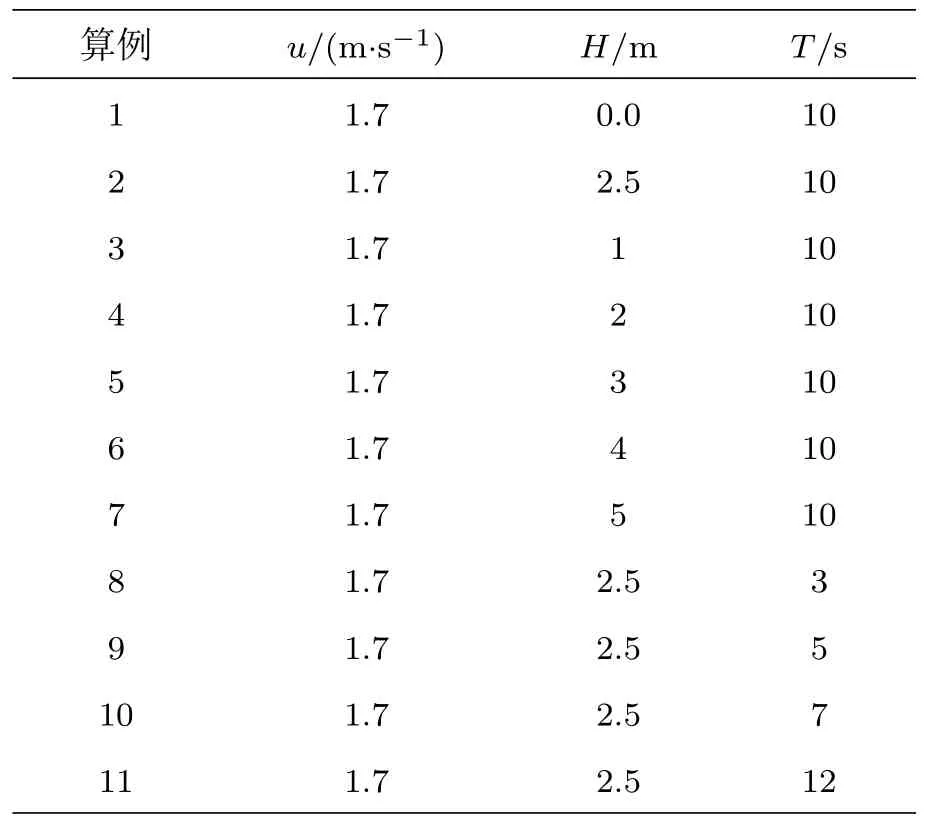
表2 计算条件及参数设置
2.2 悬链线立管形变
本文主要从悬链线立管整体变形形态、等效应力STR、位移X三方面分析悬链线立管的水动力响应及强度,其中,将整个悬链线立管上等效应力的最大值称为最大等效应力,定义为STRmax,将整个悬链线立管上位移的最大值称为最大位移,定义为Xmax。
当悬链线立管在海流和水面船作用下达到动态稳定后,针对A∼D 四个特定时刻,即A 和C 时刻对应水面船水平位移最大和最小,B 和D 时刻对应水面船垂向位移最大和最小,分别提取算例2 条件下悬链线立管变形后的形态,并与初始形态进行对比,如图3 所示。
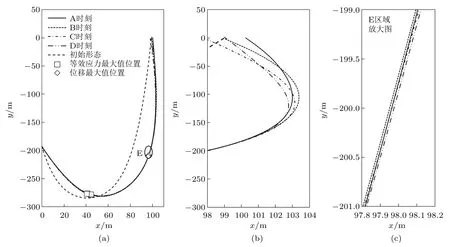
图3 悬链线立管初始形态和变形后形态对比(H = 2.5 m)
图3(a) 表明,A∼D 四个时刻对应的悬链线立管变形后形态差别较小,且悬链线立管最大等效应力和位移的位置基本相同,这缘于海流对悬链线立管的影响要大于水面船运动产生的影响。图3(b) 和图3(c) 分别为悬链线立管横向和最大位移位置处的放大图,由图3(b) 可见,水面船运动到不同位置对悬链线立管变形的影响主要集中在水面附近,且当水面船运动到最高位置时,即D 位置,悬链线立管顶端变形最小,但向下延伸到最大位移处的变形最大,如图3(c) 所示。
2.3 悬链线立管等效应力和位移的时间变化
图4(a) 表示算例2 条件下,最大等效应力和最大位移随时间变化规律。由图可见,在水面船作周期性的椭圆运动过程中,悬链线立管的最大等效应力和最大位移均随时间呈周期性变化,且变化周期与水面船运动周期相同,但最大等效应力和最大位移的极值点到达时间存在约T/2 的相位差。
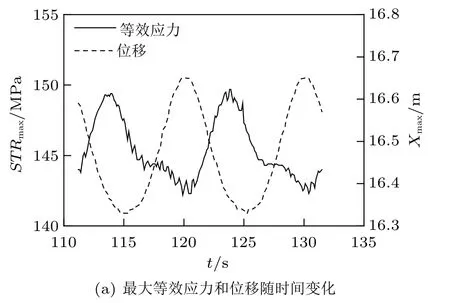
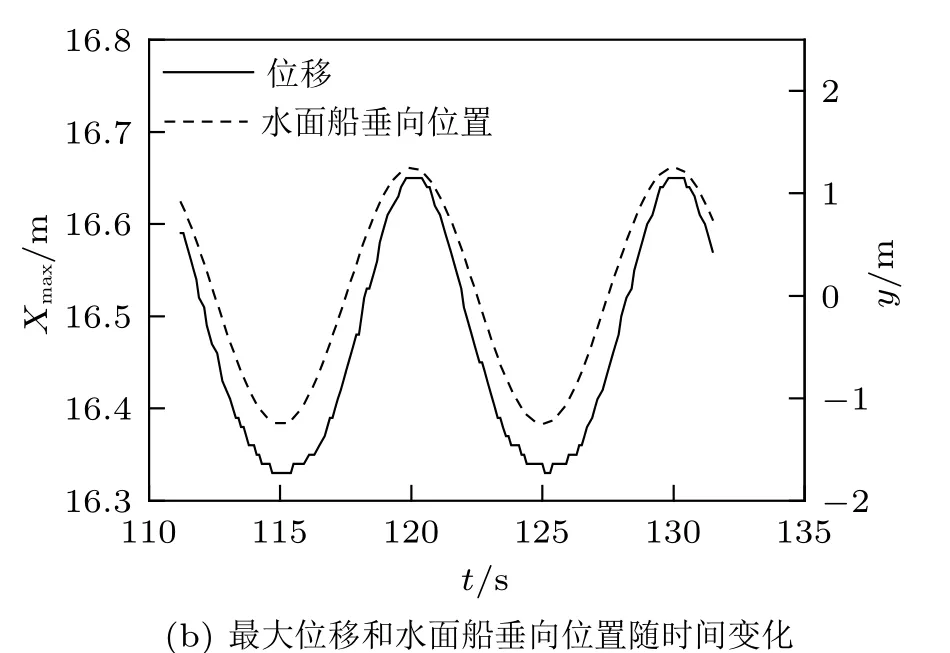
图4 等效应力和位移变化规律
为明确悬链线立管最大位移与水面船位置的对应关系,提取悬链线立管最大位移和水面船垂向位置随时间变化,绘于图4(b) 中。可以看出,当水面船运动到最高点时,悬链线立管的最大位移达到极大值;当水面船运动到最低点时,悬链线立管的最大位移达到极小值,得到的结论与图3 一致。
2.4 悬链线立管等效应力和位移的空间分布
通过分析悬链线立管等效应力和位移的空间分布,得到最大等效应力和位移的分布位置,明确悬链线立管容易发生破坏之处,对工程设计具有重要意义。
图5(a) 和图5(b) 分别表示不同水面船运动位移幅值条件下,悬链线立管等效应力和位移达到最大值时刻的分布规律,对应表2 中算例1、2 和7。由图可见,不同水面船运动位移幅值条件下,悬链线立管等效应力和位移分布规律相似,即悬链线立管两端应力(位移)较小,从两端向中间先增加后减小,存在两个极大值,且极大值的位置相近。图5(a) 表明悬链线立管最大等效应力位于x ≈40 m 位置处,且随水面船运动位移幅值增加而增加。悬链线立管最大位移位于x ≈98 m 位置处,且随水面船运动位移幅值增加而增加,如图5(b) 所示。

图5 不同水面船运动位移幅值时等效应力和位移分布
3 水动力响应和强度影响因素分析
本文主要分析水面船运动位移幅值H和周期T两个因素对悬链线立管动力响应的影响规律。
3.1 水面船位移幅值的影响
水面船运动位移幅值H表征水面船运动垂向最大距离,与水面波浪特性有关。在本文计算条件下,悬链线立管最大等效应力和最大位移与H的关系分别如图6(a) 和图6(b) 所示。由图可见,悬链线立管最大等效应力和最大位移随H增加而增加,且增长速率逐渐增加。图6(a) 表明,当水面船位移幅值从0 增加到5 m 时,悬链线立管等效应力最大增幅为14.4%,最大位移增幅可达6.1%,如图6(b)所示。结果更进一步说明,水面船运动位移幅值对悬链线立管最大等效应力的影响大于对位移的影响。
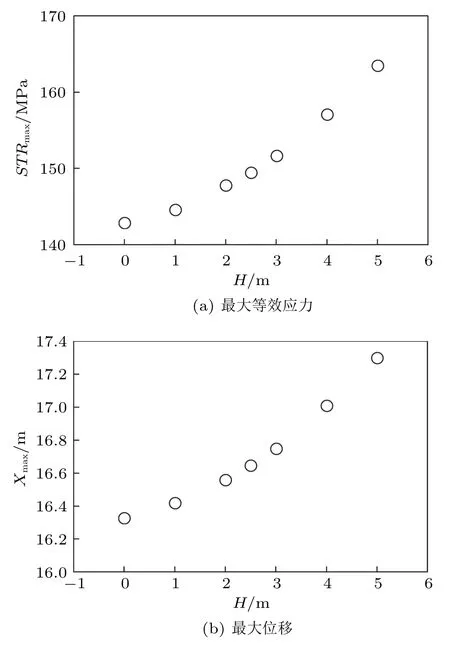
图6 水面船运动位移幅值的影响
3.2 水面船运动周期的影响
水面船运动周期是与水面波浪特性相关的又一个重要参数,其对悬链线立管等效应力和位移的影响如图7 所示。由图可见,悬链线立管最大等效应力和位移随水面船运动周期的增加而减小。当水面船运动周期从3 s 增加到12 s 时,悬链线立管等效应力的最大降低幅度为19.7%,如图7(a) 所示,悬链线立管位移的最大降低幅度为7.0%,如图7(b)所示。结果更进一步说明,水面船运动周期对悬链线立管最大等效应力的影响大于对位移的影响。

图7 水面船运动周期的影响
4 结论
以深海采矿系统悬链线立管为研究对象,同时考虑海流和水面船运动的影响,通过数值模拟的方法,研究了悬链线立管的动力响应,探讨了水面船运动对悬链线立管的影响规律,得到以下结论:
(1)悬链线立管最大等效应力和最大位移随时间均呈周期性变化,且存在半个周期的相位差。当水面船运动到最高点时,悬链线立管位移达到最大值。
(2) 悬链线立管的最大等效应力和最大位移随水面船运动位移幅值的增加而增加,且增加速率逐渐增大;而悬链线立管的最大等效应力和最大位移随水面船运动周期的增加而减小,且降低速率逐渐减小。
(3)水面船运动位移幅值和周期对悬链线立管等效应力的影响比对其位移的影响更显著。
