变刚度半被动双足机器人行走的仿人控制1)
2020-10-28张奇志周亚丽
张 瑞 张奇志 周亚丽
(北京信息科技大学自动化学院,北京100192)
1990 年,McGeer[1]研制出了只依靠重力作用并能够沿着一定的坡度向下行走的双足机器人,同时提出了被动行走概念。这种装置利用势能转换为行走的动能,从而实现周期行走。刘延柱[2]分析了人体双足步行的动态稳定性和跳跃运动的动力学过程。柳宁等[3-4]采用胞映射法对被动行走机器人的吸引域进行了研究。郑鹏等[5]引入扩展赫兹接触模型和LuGre 摩擦模型建立了被动行走机器人的动力学模型,并研究了系统关于摩擦系数的分岔与混沌现象。
纯被动行走稳定范围小,抗干扰能力差,研究者们开始转向半被动机器人领域,通过对部分关节施加驱动,使机器人能够稳定行走。由于半被动行走机器人充分利用了动力学特征,耗能少,并且与人类步态相似,引起了人们的广泛关注。Suzuki 等[6-7]采用惰性控制的方法为机器人输入必要的能量,保证刚性腿双足机器人能够在微小斜面上持续行走。
为了得到与人类走路和奔跑相似的步态,研究者们进行了大量的研究工作。Geyer 等[8]采用简单的弹簧质点模型研究双足机器人的行走步态,此模型由两个无质量的弹簧腿和一个简化的集中质量组成,称为B-SLIP(bipedal spring loaded inverted pendulum)。由于动物和人类在行走和奔跑时利用腿部驱动改变系统的能量,但是被动的B-SLIP 模型能量是不变的,不能够完全模拟实际中的步行和奔跑步态。所以为了改变系统的能量,许多研究者采用腿部驱动来调整系统的能量。其中最著名的是Raibert[9]采用一个恒定的推力改变弹簧的压缩量来改变系统的能量。Riese 等[10]通过改变自然状态下腿的长度和刚度实现不同能量级别的连续跳跃。Visser 等[11]采用输入输出状态反馈线性化进行轨迹跟踪,实现了V-SLIP(variable SLIP) 双足机器人行走。Piovan等[12]采用主动的SLIP 模型,在原本不可积分的SLIP 模型上利用部分反馈线性化的方法获得了解析解,并使用可调节的串联弹性腿部驱动器来调整腿的长度,以此改变系统的能量实现单腿机器人的连续跳跃。Hamza¸cebi 等[13]通过在髋关节添加驱动力矩和调节腿的长度来改变机器人的能量,最终实现单腿机器人的跳跃。Dadashzadeh 等[14]将主动的SLIP作为参考模型,采用两级控制策略在ATRIAS 双足机器人上实现了行走。
传统双足行走大多采用轨迹跟踪控制方法[11-15],先结合各种优化目标生成机器人的运动轨迹,然后再跟踪轨迹。在跟踪控制过程中,控制器会产生较大的驱动力,能量效率不高,而人类行走大部分时间是近似无源的[16]。并且人类行走通过后腿蹬地控制系统能量,防止向后倾倒;通过前腿触地位置控制高度和前向运动速度,防止向前倾倒。因此通过观察人类行走模式,本文提出了一种能量高效、步态自然的模仿人类行走的控制策略,只在双支撑开始阶段调整后腿刚度使机器人的总能量接近期望值,在单支撑阶段通过摆动腿触地位置控制机器人的高度和前向速度。机器人大部分时间处于无源状态,利用自身的动力学特性实现零输入的纯被动周期行走。
1 双足机器人动力学模型
1.1 机器人模型
变刚度双足弹簧负载倒立摆模型是在双足弹簧负载倒立摆模型的基础上,将弹簧刚度由K0变为K0+u,引入了刚度控制输入量u,其模型[11]如图1 所示。

图1 变刚度双足机器人行走模型图
假设所有关节质量都集中在髋关节,同时忽略关节摩擦的影响。定义系统的广义坐标为q=[x,y],所以系统的状态可以由z表示
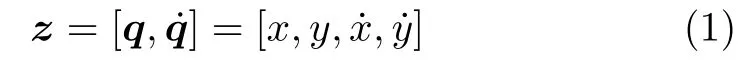
假设机器人单步行走从单腿支撑并且方向垂直于水平面的V LOi状态开始,当质点运动到下一个V LOi+1状态时结束,如图1 所示,此过程由单腿支撑和双腿支撑两个阶段组成。
假设机器人所有质量集中在髋关节,质量为m,并且两条腿没有质量,同时假定脚与地面无相对滑动。L0为腿在自然状态下的原长,后腿L1为支撑腿长度,前腿L2为摆动腿长度,弹簧在自然状态下的刚度系数为K0,摆动腿触地时和地面的夹角为α,g代表重力加速度,u1和u2分别为支撑腿和摆动腿的刚度控制量,可在机器人行走过程中改变。为了使腿的刚度更加贴近实际情况,对双腿刚度控制量ui作如下限制
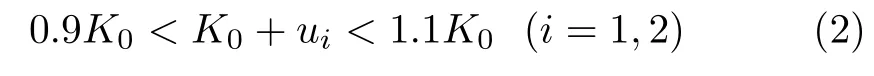
1.2 系统动力学方程
采用拉格朗日方法可以得到双足机器人行走的动力学方程。系统拉格朗日函数为

其中K(q,q,) 是系统动能,P(q) 是系统势能。
系统的拉格朗日方程为

式中,Fi为施加到质点上的广义力。
通过计算图1 所示该系统的动能和势能,可得拉格朗日函数表达式为

式中

式中,a为摆动腿触地点的x坐标值。
将式(5) 和式(6) 代入到式(4) 中,可得系统双支撑阶段的动力学方程

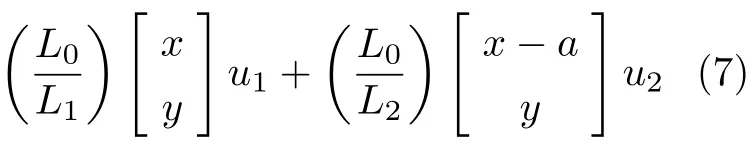
式(7) 去掉和前腿相关的项可以得到单支撑阶段动力学方程

当机器人从双支撑切换到单支撑时,切换条件为支撑腿到达原长,并且脚的速度向上,即

当机器人从单支撑切换到双支撑时,切换条件为质点高度到达H,并且脚的速度向下,即

2 双足机器人行走控制算法
假设纯被动双足机器人以给定初值在V LOi状态开始行走,如图1 所示,当机器人运动到下个VLO(vertical leg orientation) 状态时为V LOi+1。若要使机器人实现周期行走,即保证

其中
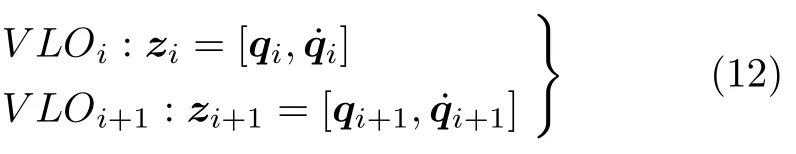
由此可以得到机器人周期行走的不动点

传统的行走控制以z∗为初值,利用近似解析解或数值近似解方法得到期望轨迹,再采用轨迹跟踪控制方法实现双足机器人的周期行走控制。为了保证系统的性能,一般闭环系统具有较高的刚度。即使没有外界干扰,由于近似解得到期望轨迹与真实解存在误差,跟踪控制需要较大的控制力,能量效率不高。文献[8] 表明,在能量守恒的前提下,系统是自稳定的,即在小扰动条件下,不需要外界控制自动回到周期行走状态。因此,可以利用系统的自稳定特性,设计控制器保证系统能量不变,进而实现双足机器人的稳定行走。
周期行走时机器人系统的总能量E∗为
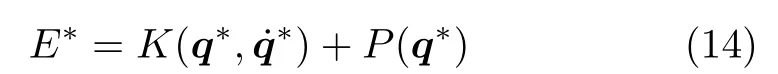
机器人在行走时具有的总能量E(t)

式中,∆L1和∆L2分别为腿长L1和L2的形变量
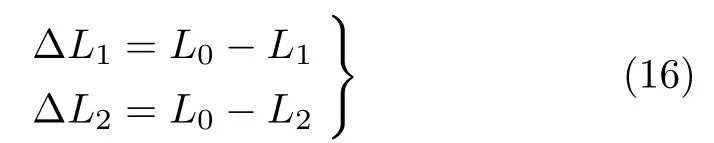
在遇到外界扰动时,为保持机器人稳定行走,需要给机器人增加或者减少能量。本文模拟人类行走后腿蹬地补充能量行为,采用在双支撑初始时刻只对后腿刚度施加变刚度控制u1,前腿刚度K0保持不变的控制策略。
令E∗=E(t),联立式(14) 和式(15),解得

在单支撑阶段采用固定的触地角可以实现稳定行走[8]和奔跑[17],为了提高行走的鲁棒性,采用Seyfarth 等[18]提出的模拟人类跑步的摆动腿常角速度转动方法控制触地位置的方法。在机器人行走过程中,单支撑阶段摆动腿的触地角度α(t) 为

式中,α0为初始角度,ω为摆动角速度,tVLO为支撑腿位于竖直位置时的时间。
由于在单支撑阶段只是通过调节摆动腿的触地角度,同时忽略了腿的质量,因此系统在单支撑阶段的总能量是不变的。摆动腿匀速转动自动调节集中质量的高度和前向速度,进而稳定到周期行走状态。
双支撑阶段初始时刻改变后腿刚度和单支撑阶段采用摆动腿匀速转动,构成了双足机器人仿人行走控制策略。当机器人在期望能量E∗下周期行走时,双腿的刚度则恢复为K0,使机器人仅依靠系统的动力学特性实现机器人零输入的周期行走。
3 仿真验证
实验仿真在软件MATLAB 中进行,由于动力学方程具有非线性特性,采用4 阶龙格库塔法进行数值计算,仿真时间间隔为1 ms, 其中m=80 kg,K0=15 696 N/m,L0=1 m,α=70◦,g=9.81 m/s2。根据上述系统参数[15]得到一组机器人周期行走的初值z∗=[0,0.999,1.172,0],计算得到系统具有总能量E∗= 838.964 4 J。单支撑阶段摆动腿转动控制策略使用的控制参数α0=75◦,ω=−49(◦)/s。
纯被动行走机器人采用上述参数在VLO 状态进行60 步行走仿真,在第30 步至第32 步行走的单支撑阶段过程中施加外部扰动力F=(−20,20)TN,从图2 中可以看出,受干扰后机器人的总能量急剧减小,水平速度降低,进而摔倒。
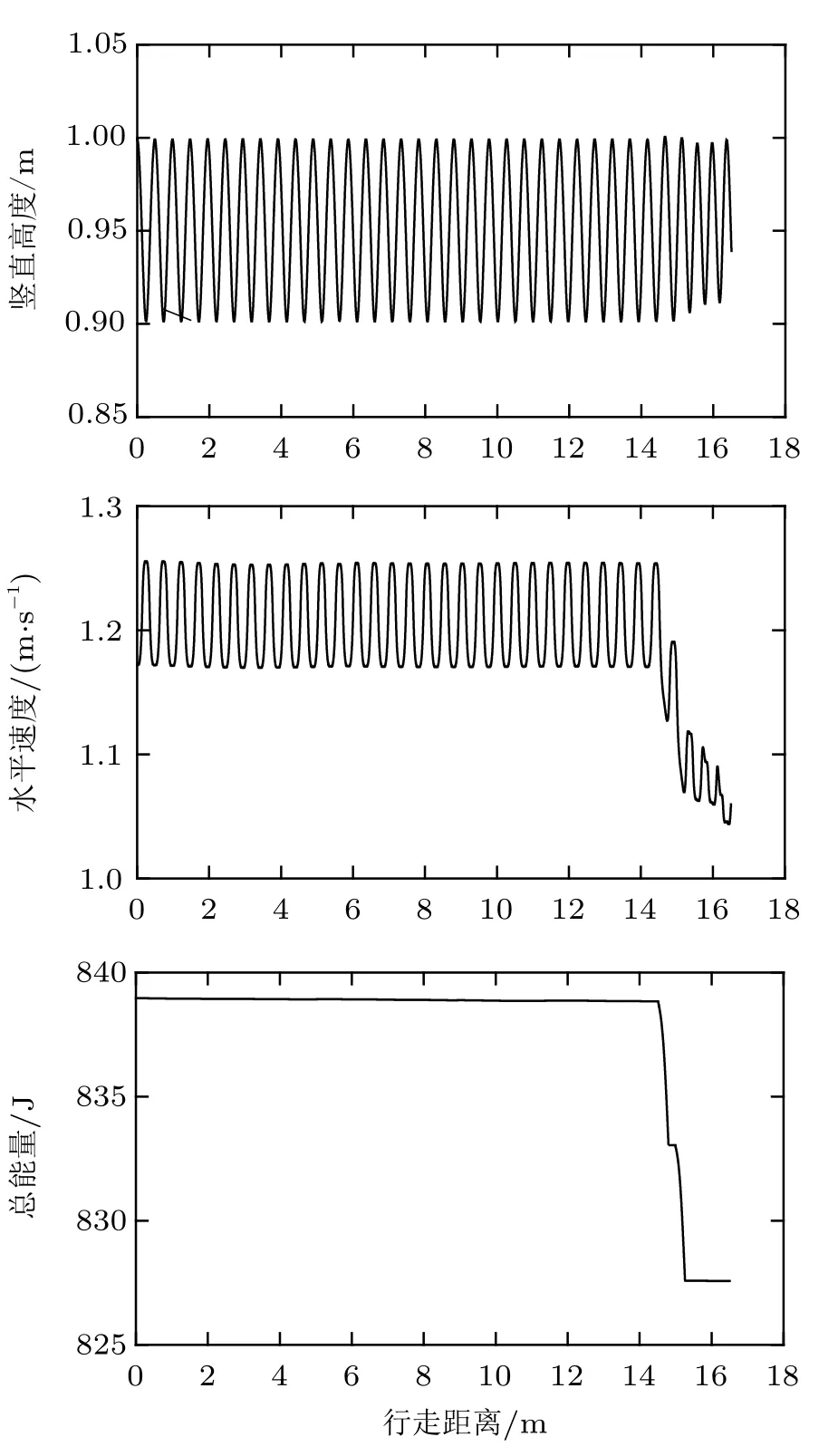
图2 施加扰动下纯被动系统状态随行走距离变化曲线

图2 施加扰动下纯被动系统状态随行走距离变化曲线(续)
为了考察仿人行走控制策略的效果,下面分别对只采用双支撑阶段的能量控制和单支撑段的摆动腿控制进行仿真。
同样施加上述扰动,只在双支撑的初始阶段进行能量控制,系统状态随行走距离变化曲线如图3所示。从图3 中可以看出,系统的能量能够逐渐恢复到E∗附近,但是质点的水平速度急剧上升,质点高度减小,最后倒下。因此,可以得出结论:行走过程中在双支撑阶段初始时刻采用的能量控制器产生了作用,但是不足以使系统稳定,不能使机器人稳定行走。
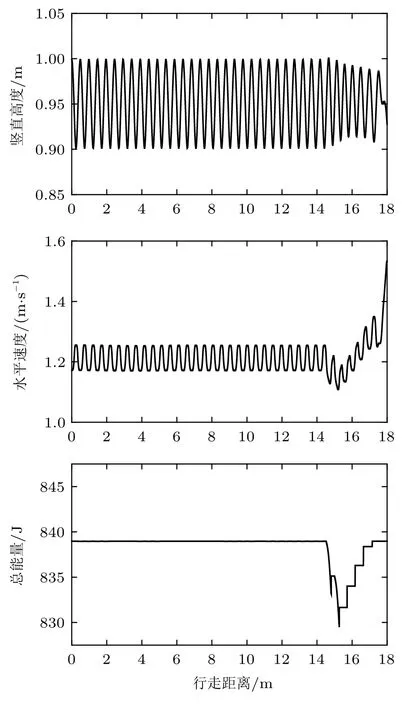
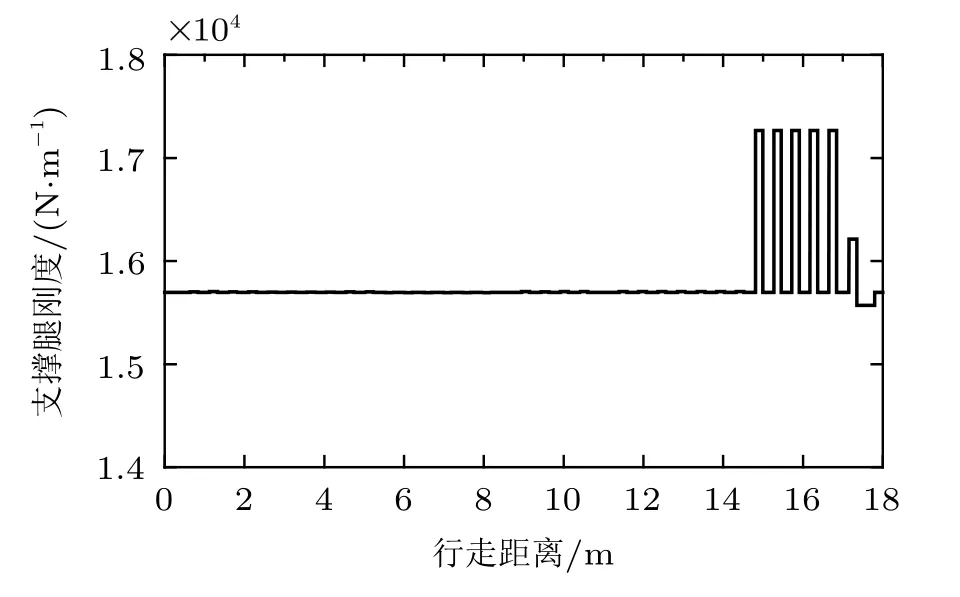
图3 施加扰动能量控制下系统状态随行走距离变化曲线
只采用单支撑阶段的摆动腿控制策略,采取同样的扰动进行仿真,系统状态随行走距离变化曲线如图4 所示。由于单支撑阶段系统是保守系统,控制器并没有对系统的能量进行改变,只是调节了质点的水平速度和高度。在施加外部扰动后,质心的高度和前向速度都下降。因此,可以得出结论:在行走过程中采用摆动腿控制方法调节了集中质量的前进速度和高度,但是仍然不能稳定系统。

图4 施加扰动摆动腿控制下系统状态随行走距离变化曲线

图4 施加扰动摆动腿控制下系统状态随行走距离变化曲线(续)
由此可见,单独采用能量控制和摆动腿控制策略并不能使机器人稳定行走,因此下面结合两个控制器的优点,使用完整的仿人控制策略对系统进行仿真。采取同样的参数,仿真结果如图5 所示。从图中可以看出,施加扰动后,系统能量经过多步调整逐渐恢复到期望值附近,质点的高度和前向速度恢复到周期状态。由于对变刚度进行了限幅,控制器则出现了饱和,如果不限幅,系统可以更快地恢复到周期行走状态。


图5 施加扰动仿人控制下系统状态随行走距离变化曲线
由此可见,仿人行走控制策略可以抵抗外界扰动,消除扰动后的系统能量,最终稳定在期望值附近;在没有干扰后,机器人恢复被动周期行走。结果表明仿人行走控制策略对于外界干扰具有鲁棒性。
4 结论
本文针对变刚度半被动双足机器人行走控制问题,提出了仿人行走控制策略。此策略不需要事先规划机器人的运动轨迹,并且充分利用系统的动力学特征,只在系统受到干扰时进行变刚度控制,没有干扰时不需要外界输入,仅依靠自身的动力学特性实现纯被动周期行走。在MATLAB 仿真平台上进行了验证,仿真实验结果验证了仿人行走控制策略的有效性,且控制系统对于外界干扰具有鲁棒性。
本文所提出的方法在快速响应和减少系统能量输入上具有一定的优势,可以为设计高效的类人步态行走控制器提供参考。在本文理论研究和实验基础上进行硬件实验平台的验证是需要进一步研究的课题。
