中心极限定理教学及应用研究

李宝娜 朱 平

（洛阳师范学院数学科学学院 河南·洛阳 471934）

0 引言

概率论与数理统计是研究自然界中随机现象数量规律性的一门学科，最早产生于17世纪中叶的赌博行为，并以此发展起来。概率论是研究随机现象的统计规律性，而数理统计研究如何从样本分布估计总体分布.大多数的概率统计教材中，概率论最后一个章节便是大数定律和中心极限定理，中心极限定理表达的是确定在什么条件下，大量随机变量之和的分布逼近于正态分布。可以这样说，正因为有了这类定理，自然界的许多符合正态分布的随机现象有了坚实的理论基础。

1 教与学的分析

中心极限定理（Central Limit Theorems）是概率论中论证随机变量和的极限分布为正态分布的定理的总称。中心极限定理的教学安排在随机变量、分布函数等内容之后，抽样分布、假设检验等统计学内容之前，从这个意义上来看，中心极限定理是概率论和数理统计两部分的衔接，起着承上启下的作用；从内容上来说，中心极限定理的数学表达具有抽象性，理论性较强，短时间内理解起来比较困难。如果从纯理论角度来讲解会加大学习的难度；从学情分析，概率论与数理统计为专业基础课，数学院的学生主要在大二上学期学习.对于步入大学的第二年，有一定的学习能力和专业基础，对大学学习和生活已经基本适应，学习积极性比较高，但是学习方法掌握的不够多，学习深度不够强，尤其是对于理论性较强的缺乏实践认知。

本文立足内容难度和学情分析，先从生活中的现象讲起，实验模拟，引出中心极限定理表达内容，最后通过具体事例阐明中心极限定理的应用.将抽象的内容更加形象化和具体化，开阔了学生的视野，缓解了学生的畏难情绪，从而达到良好的教学效果。

2 教学设计

2.1 问题导向-随处可见的正态分布

生活中，我们会有这样一个经验性认知：中间状态是事物的常态，过高和过低都属于少数.也就是我们数学中的正态分布所描述的现象，比如人群的身高、寿命、血压、考试成绩、测量误差、员工回家所需要的时间、某城市的耗电量等等，都符合正态分布.我们不仅要问一句：为什么？

在回答问题之前，我们先利用python进行模拟实验：

2.1.1 数据生成

假设我们现在在观察一个人掷均匀的骰子，得出的结果1-6的概率都是相同的1/6，他掷了20000次。现在我们来模拟下掷骰子的结果：

生成出来的平均值：3.49525

生成出来的标准差：1.6982866181831617

由于骰子点数服从均匀分布，平均值接近3.5符合理论值。

2.1.2 画图

生成的数据用直方图画出来如下：

2.1.3 抽样

接下来随便抽取一组数据，例如，从生成的数据中随机抽取10个数字.这10个数的结果是：[6 1 2 1 4 3 1 3 1 6]

生成出来的平均值：2.8

生成出来的标准差：1.8867962264113207

可以看到，只抽取少量样本的时候，样本的平均值（2.8）会距离总体的平均值（3.5）偏差较大。

2.1.4 中心极限定理的体现

现在我们抽取20，200，2000，20000 组，每组50个.每组的平均值都计算出来，直方图如图1。

我们看到投掷20000个骰子点数的平均值符合概率理论结果，当观察每组50的平均值时我们发现抽样次数比较少时，平均值的分布没有规律，但随着抽样的增加，取2000组甚至更多时，可以看到平均值的分布近似为正态分布，基本符合大多数为中间状态（3.5附近），靠近1和6的可能性明显很低。

2.2 中心极限定理

由上述的实验可以看到，随着抽样的增加，极限分布趋近于正态分布。这便是中心极限定理所表达内容。由于中心极限定理是一类描述和的极限分布为正态分布的定理，我们接下来主要介绍常见的三个中心极限定理。

图1

定理三（棣莫弗-拉普拉斯（De Moivre-Laplace）定理）设随机变量服从参数为n，p（0＜p＜1)的二项分布，那么对于任意的x即有

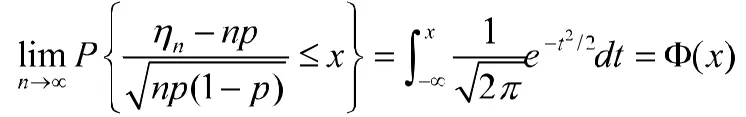
2.3 中心极限定理的应用

设有100个年龄为x岁且相互独立的被保险人都投保了保险金额为10元的终身寿险，随机变量剩余寿命T的概率密度。保险金于被保险人死亡时进行给付，保险金给付是从某基金中按照利息强度支付。计算这项基金在最初的数额至少是多少时，才能保证从这项基金中足以支付每个被保险人的死亡给付的概率达到95%？

由于对每个被保险人都有

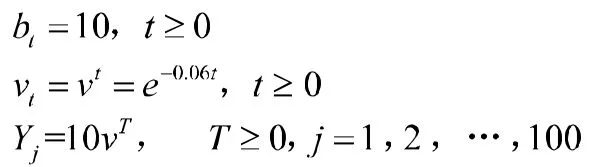
所以，该基金在最初时至少为449.35元，比收取的趸缴纯保费总额400元多出49.35元。

3 总结

中心极限定理为一类定理的统称。中心极限定理表明，在较为一般的条件下，当独立随机变量的个数不断的增加时，和随机变量的分布趋近于正态分布。一方面，中心极限定理可以解释为什么正态分布在生活中很常见；另一方面，中心极限定理是大样本统计推断的理论基础。不管是从名称来源、教学地位还是教学内容，中心极限定理都占有重要的位置。本文突出从形象易懂掷骰子的例子出发引导学生理解中心极限定理所表达的含义，通过图示直观感受，并以实际保险为练习强化对中心极限定理的理解和应用，以期学生能够对中心极限定理有更加全面、准确的认识。