椭圆曲线y2=nx(x2+256)整数点解的分布

李 娇,杨 海,董 鑫

(西安工程大学 理学院,陕西 西安 710048)

0 引言与主要结果

椭圆曲线的整数点问题是数论中很重要的研究课题之一。关于椭圆曲线

y2=nx(x2+a),n,a∈Z+

(1)

的整数点问题,目前已经有不少的研究成果,但该问题尚未彻底解决。

当a=1时,祝辉林等证明了当n为素数时,椭圆曲线(1)至多有一个正整数解[1];管训贵运用W. Ljunnggren关于四次Diophantine方程的结果给出了n=Fn时,椭圆曲线(1)的整数解为(x,y)=((Fn-2-1)2,Fn(Fn-2-1))[2];杨海等证明了n为奇素数时椭圆曲线(1)整数解的情况以及该曲线有整数点的2个判别条件[3];乐茂华运用初等数论的方法证明了n=p(p为素数)时椭圆曲线的整数点分布[4];窦志红证明了n=2p时椭圆曲线(1)的所有整数解[5]。

当a=2时,廖思泉等运用四次Diophantine方程改进的解数上界，证明了当n=p时椭圆曲线(1)至多有2组正整数解[6];杜晓英通过运用丢番图方程的已知结果，证明了当n=p≡1(mod 8)时椭圆曲线(1)没有正整数点[7];张瑾给出了当n为素数时椭圆曲线(1)整数解的情况[8];陈历敏证明了当n为奇数时椭圆曲线(1)的整数解的情况[9];李玲等证明了当n是大于1的无平方因子的正奇数时，椭圆曲线(1)仅有整数解(x,y)=(0,0)[10]。

当a=2m(2≤m≤7,m∈N)时，文献[11-20]分别给出了椭圆曲线(1)的整数解的分布情形。从已有的研究结论来看,通过对此类椭圆曲线方程不同参数的取值寻找规律,探寻其一般性的方法和结论是有意义的。但是，随着参数取值的增加，计算难度会更大,甚至出现用已有的方法无法计算其整数点问题。同时，由于选取参数的不同,求解方法迥异,这些结论也没有明显的关联性。鉴于此,本文利用同余、勒让德符号值的性质及初等数论方法,给出了当a=256且n为无平方因子的正奇数时,椭圆曲线y2=nx(x2+256)整数点的分布情况，得出如下结果：

定理1如果n是无平方因子的正奇数,且n的所有素因子qj(j∈Z+)满足qj≡3,7(mod 8),则椭圆曲线

y2=nx(x2+256)

(2)

当n≠3时,仅有一个整数点(x,y)=(0,0);当n=3时,仅有2个整数点(x,y)=(0,0)和(x,y)=(12,120)。

1 定理1的证明

显然,(x,y)=(0,0)是椭圆曲线(2)整数点。设(x,y),x,y∈Z+是椭圆曲线(2)的正整数点,因为n是无平方因子的正奇数,故由式(2)知n|y。设y=nz,z∈Z+,代入式(2),得

nz2=x(x2+256)

(3)

因为gcd(x,x2+256)=gcd(x,256)=1,2,4,8,16,32,64,128,256,设a,b∈Z+,式(3)可分解为以下9种情形:

情形1:x=pa2,x2+256=qb2,z=ab,n=pq,gcd(a,b)=1;

情形2:x=2pa2,x2+256=2qb2,z=2ab,n=pq,gcd(a,b)=1;

情形3:x=4pa2,x2+256=4qb2,z=4ab,n=pq,gcd(a,b)=1;

情形4:x=8pa2,x2+256=8qb2,z=8ab,n=pq,gcd(a,b)=1;

情形5:x=16pa2,x2+256=16qb2,z=16ab,n=pq,gcd(a,b)=1;

情形6:x=32pa2,x2+256=32qb2,z=32ab,n=pq,gcd(a,b)=1;

情形7:x=64pa2,x2+256=64qb2,z=64ab,n=pq,gcd(a,b)=1;

情形8:x=128pa2,x2+256=128qb2,z=128ab,n=pq,gcd(a,b)=1;

情形9:x=256pa2,x2+256=256qb2,z=256ab,n=pq,gcd(a,b)=1。

分别讨论这9种情形下椭圆曲线(2)的正整数点的情况。

情形1将x=pa2代入x2+256=qb2,得

p2a4+256=qb2

(4)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8),对式(4)两边取模qj,得

p2a4≡-256(modqj)

(5)

因为qj≡3,7(mod 8),故Legendre符号

所以式(5)不成立,则式(4)不成立,因此q>1时情形1不成立。

ⅱ) 当q=1时,n=p,由x2+256=b2得b2-x2=256,解得(b,x)=(65,63),(34,30),(20,12),(16,0)。由x=na2得,na2=63,30,12,0;又n≡3,7(mod 8)为奇素数,故na2=12,0,即n=3,a=2。所以x=3a2,即(x,y)=(12,120)是椭圆曲线(2)的一个整数点。

情形2将x=2pa2代入x2+256=2qb2,得

2p2a4+128=qb2

(6)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(4)两边取模qj,得2p2a4≡-128(modqj),即

p2a4≡-64(modqj)

(7)

因为qj≡3,7(mod 8),故Legendre符号

所以式(5)不成立,则式(4)不成立,因此q>1时情形2不成立。

(8)

因为n是奇数,a是奇数,则式(8)左边为奇数;但b是偶数,则式(8)右边为偶数。显然等式不成立,所以当q=1时,情形2不成立。

情形3将x=4pa2代入x2+256=4qb2,得

4p2a4+64=qb2

(9)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(9)两边取模qj,得4p2a4≡-64(modqj),即

p2a4≡-16(modqj)

(10)

因为qj≡3,7(mod 8),故Legendre符号

所以式(10)不成立,则式(9)不成立,因此q>1时情形3不成立。

情形4将x=8pa2代入64x2+256=8qb2,得

8p2a4+32=qb2

(11)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(11)两边取模qj,得8p2a4≡-32(modqj),即

p2a4≡-4(modqj)

(12)

因为qj≡3,7(mod 8),故Legendre符号

所以式(12)不成立,则式(11)不成立,因此q>1时情形4不成立。

ⅱ) 当q=1时,n=p,此时式(11)可化为

8n2a4+32=b2

(13)

则b为偶数,所以b2≡0,4(mod16);又因为gcd(a,b)=1,则a为奇数。对式(13)两边取模16,得8≡8n4a4+32=b2≡0,4(mod 16),显然不成立。则式(13)不成立,故式(11)不成立。所以当q=1时,情形4不成立。

情形5将x=16pa2代入x2+256=16qb2,得

16p2a4+16=qb2

(14)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(14)两边取模qj,得16p2a4≡-16(modqj),即

p2a4≡-1(modqj)

(15)

因为qj≡3,7(mod 8),故Legendre符号

所以式(15)不成立,因而式(14)不成立,因此q>1时情形5不成立。

情形6将x=32pa2代入x2+256=32qb2,得

32p2a4+8=qb2

(16)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(16)两边取模qj,得32p2a4≡-8(modqj),即

4p2a4≡-1(modqj)

(17)

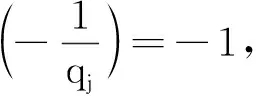
ⅱ) 当q=1时,n=p,此时式(16)可化为

32n2a4+8=b2

(18)

可得4|b。令b=4c,c∈Z+,则式(18)可化成2c2-4n2a4=1。显然等式无解,所以式(18)不成立,则式(16)不成立,所以当q=1时,情形6不成立。

情形7将x=64pa2代入x2+256=64qb2,得4 096p2a4+256=64qb2,即

64p2a4+4=qb2

(19)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(19)两边取模qj,得64p2a4≡-4(modqj),即

16p2a4≡-1(modqj)

(20)

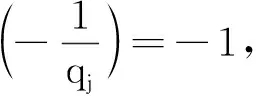
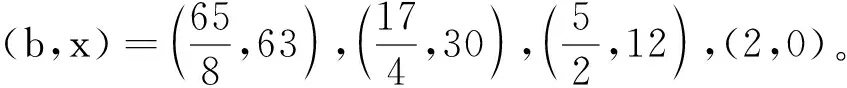
情形8将x=128pa2代入x2+256=128qb2,得16 384p2a4+256=128qb2，即

128p2a4+2=qb2

(21)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(21)两边取模qj,得128p2a4≡-2(modqj),即

64p2a4≡-1(modqj)

(22)

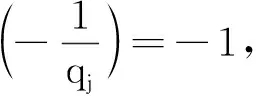
ⅱ) 当q=1时,n=p,此时式(21)可化为

128n2a4+2=b2

(23)

则b为偶数,所以b2≡0,4(mod 16); 又因为gcd(a,b)=1,则a为奇数。对式(23)两边取模16，得2≡128n4a4+2=b2≡0,4(mod 16),显然不成立,则式(23)不成立,因而式(21)不成立。所以当q=1时,情形8不成立。

情形9将x=256pa2代入x2+256=256qb2,得65 536p2a4+256=256qb2，即

256p2a4+1=qb2

(24)

ⅰ) 当q>1时,q中至少含有一个素因子qj,j∈Z+,由题意得qj≡3,7(mod 8)。对式(24)两边取模qj,得

256p2a4≡-1(modqj)

(25)

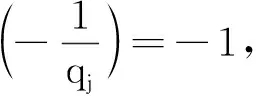
ⅱ) 当q=1时,n=p,由x2+256=256b2得(16b)2-x2=256,解得

由x=na2，得na2=1,0;又n≡3,7(mod 8)为奇素数,故无解。因此,当q=1时情形9无解。

综上所述,定理1得证。