非对称结构形状记忆合金梁模型的混沌运动
2020-10-23沈晓娜冯进钤任一凡
沈晓娜,冯进钤,任一凡
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
在日常生活中存在大量的非光滑因素,如碰撞、摩擦等。这些非光滑因素会对人们的生活产生积极,或消极的影响。因此,对于非光滑系统的研究是很有必要的。其中碰撞振动系统是一种典型的非光滑系统。HOLMES和SHAW最早对线性碰撞振动系统做了大量的研究工作。HOLMES通过一个简单的弹跳小球的实验,发现系统存在Smale马蹄混沌等丰富的动力学现象[1];SHAW对周期激励下的线性碰撞振子进行稳定性和分岔分析[2]。至今,人们对碰撞振动系统的研究已有几十年的历史,主要研究系统的周期运动和稳定性、分岔和混沌等[3]。
混沌是非线性动力系统的一种重要运动形式[4-5]。目前,关于混沌研究的解析方法主要有Shilnikov方法和Melnikov方法2种。其中Melnikov方法是一种扰动方法[6],最初由MELNIKOV于1963年提出,主要应用于光滑系统[7]。后来经HOLMES、WIGGINS等的补充和推广,用来证明稳定流形和不稳定流形横截同宿点的存在性,从而可能导致Smale意义下的混沌[8-9]。
SHAW通过对一类碰撞振动系统的研究,将Melnikov方法由光滑系统推广到非光滑系统[10];CHOW等利用Melnikov方法分析了线性碰撞系统的全局分岔和混沌[11-12]。DU利用Melnikov方法讨论了一类非线性碰撞振子的同宿分岔[13]。文献[14]讨论了谐和激励下带平方非线性项的单边碰撞系统的同宿分岔;文献[15]通过Melnikov方法分析了具有分数阶导数的Duffing系统的混沌现象;文献[16]研究了分段Hamiltonian系统的二阶Melnikov函数;文献[17]讨论了高阶Melnikov函数。由于噪声普遍存在于工程实际模型中,Melnikov方法被逐渐应用到随机情况下。XU等将Melnikov方法推广到了随机振动中[18-19];SHI应用Melnikov方法分析了Josephson系统的混沌和分叉[20]。文献[21]利用随机Melnikov方法分析了有界噪声激励下Josephson系统的运动;文献[22]利用Melnikov方法研究了有界噪声激励下碰撞振动系统的混沌运动。
上述关于非光滑系统的Melnikov方法主要集中在对称约束情形,对于单边约束情形下的Melnikov方法以及混沌运动研究甚少。本文考虑具有单边约束的形状记忆合金梁模型,该模型是典型的具有非对称结构的碰撞振动系统。利用Melnikov方法分别得到系统非光滑同宿分叉和光滑同宿分叉出现Smale马蹄混沌的必要条件,同时讨论了碰撞恢复系数、谐和激励幅值等参数对该系统的影响。
1 合金梁模型
考虑谐和激励下单边碰撞振动系统,非对称结构的形状记忆合金梁模型所遵循的方程为
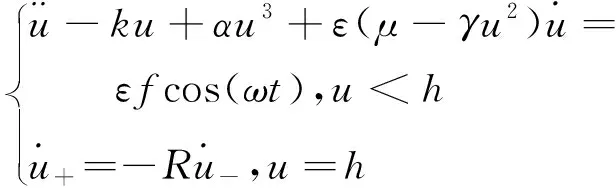
(1)
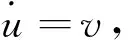
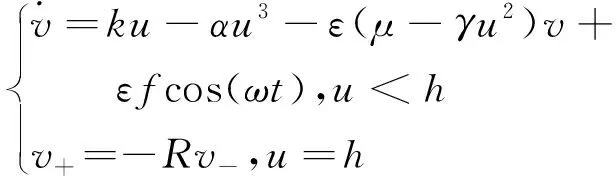
(2)
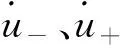
2 未扰系统的同宿轨
令系统(2)中的ε=0时,得到一个未扰系统
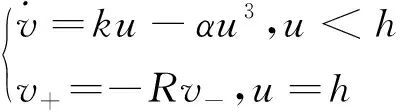
(3)
其对应的势函数为

(4)
Hamilton函数为
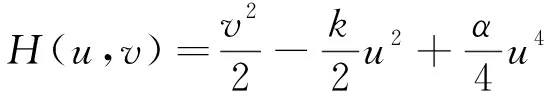
(5)
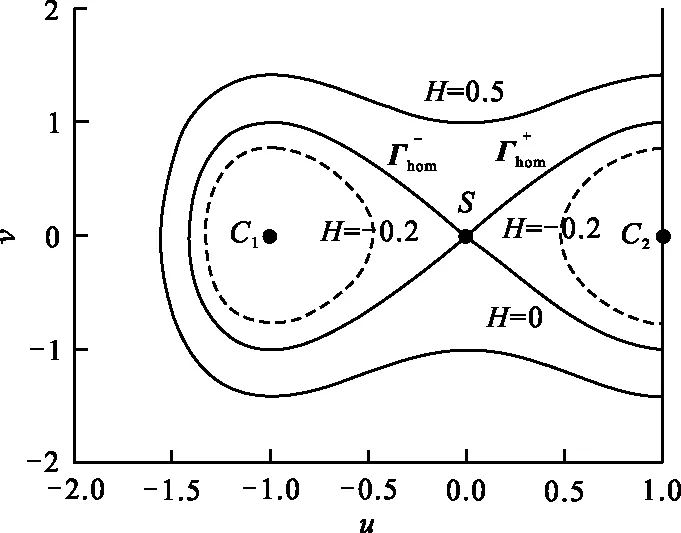
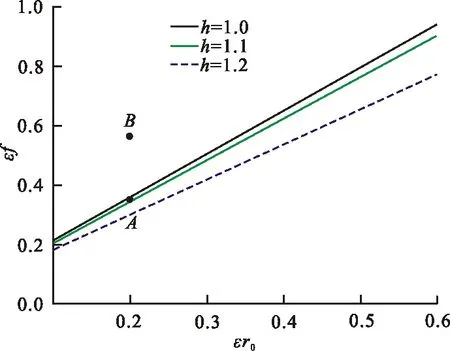
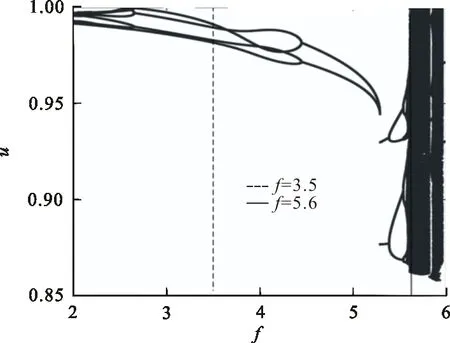
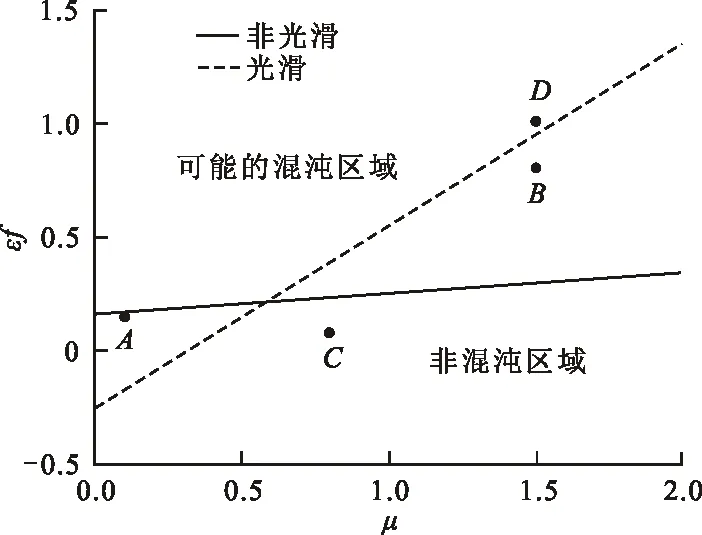
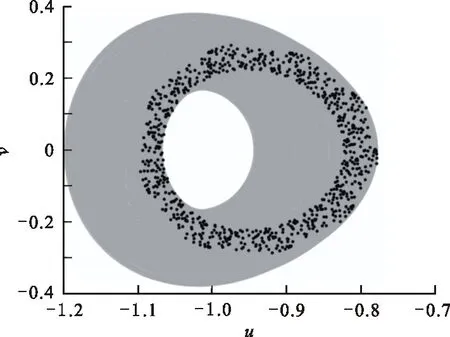
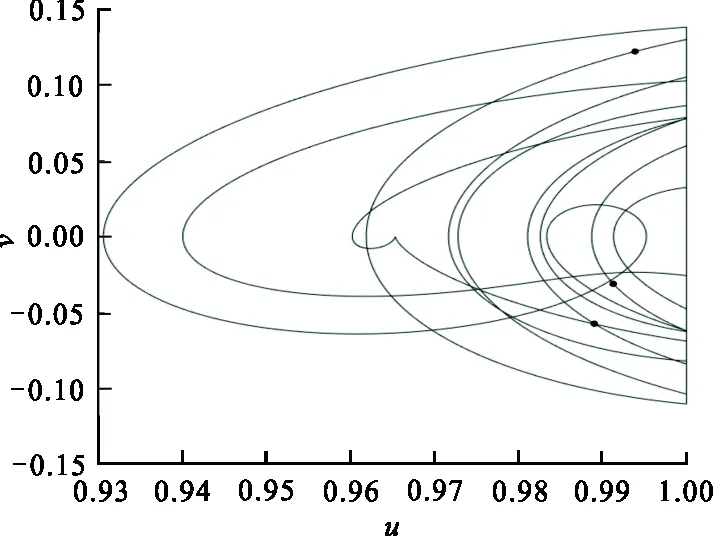
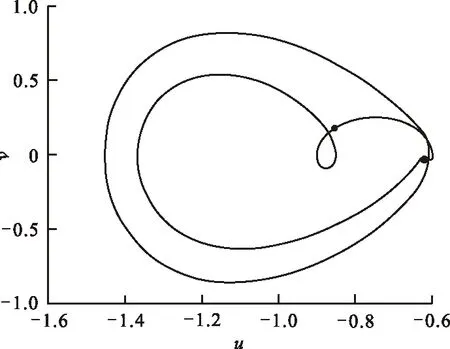
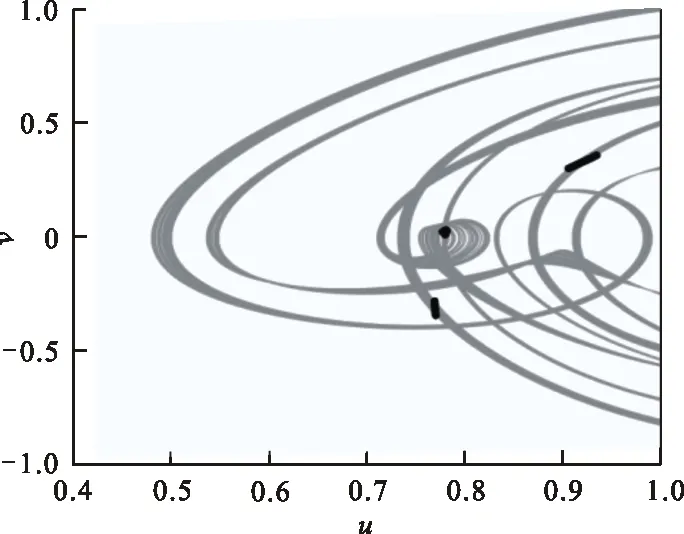
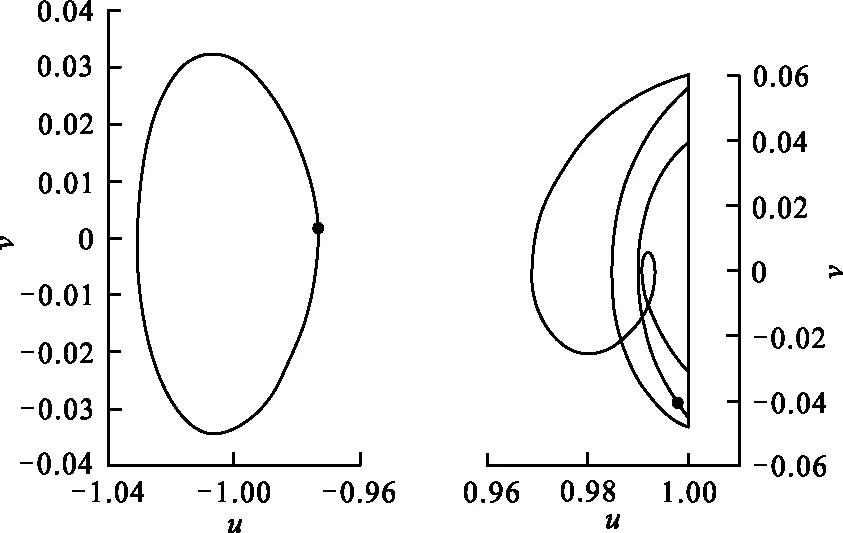
由u 2) 系统存在两条连接鞍点S(0,0)的同宿轨 (6) (7) 式中: 令式(5)中参数k=2.0,α=2.0,h=1.0,作出不同Hamilton量值在相平面上的轨线,如图1所示。图1中S为鞍点,C1、C2为中心点,黑色实线代表连接鞍点的两条同宿轨。 图 1 未扰系统(3)的同宿轨Fig.1 The homoclinic orbits of the unper- turbed system (3) 通过Melnikov理论,可以得到系统(2)的Melnikov函数。由于此系统是单边约束的不对称结构,因此分2部分计算系统(2)的Melnikov函数。 M(t0)=γA1-μA2+fA3-r0A4 (8) 式(8)中A1、A2为阻尼项,推导如下: 式(8)中A3为谐和激励项,推导如下: (11) 令 则 A3=2sin(ωt0)[sin(ωT0)W1-cos(ωT0)W2] (12) 式(8)中A4为碰撞项,推导如下: (13) 根据Smale-Binkhoff定理知,当Melnikov函数存在简单零点时,临界条件为 (14) 由式(14),得到系统(2)右侧出现Smale马蹄意义下混沌的必要条件为 (15) M(t0)=γB1-μB2+fB3 (16) 式中:B1、B2为阻尼项;B3为谐和激励项。推导如下: (17) (18) -2sin(ωt0)W4 (19) (20) 同理,根据式(14),得到系统(2)左侧出现Smale马蹄混沌的必要条件为 (21) 为了验证解析结果(式(15)、(21))的正确性,分为几个部分进行数值仿真。 图 2 h取不同值时εf随εr0变化的 Melnikov临界线Fig.2 Melnikov critical line when h takes different values 从图2可以看出,固定参数h,f随着r0的增大而增大。从能量的角度分析,因为r0越大,系统损耗的能量就越大,而外激励能够为系统提供能量,促进振子的运动。同时可以看出,在r0不变的情况下,h越大,临界值f越小,表明较大的h有助于系统混沌的生成。 在h=1.0,εr0=0.2时,临界值εf≈0.36。为验证此条件下Melnikov方法推导的必要条件的正确性,在图2中取临界值之下的点A(0.2,0.35),在上述条件下作出系统右侧的相图及Poincare截面图,如图3(a)所示。从图3(a)可以看出,系统右侧运动较为规则,且Poincare截面图只有4个点。计算其对应的最大Lyapunov指数λ,得λ≈-0.13<0,可判定此条件下系统右侧作非混沌运动。 在图1中取临界值之上的点B(0.2,0.56),作出系统右侧的相图,Poincare截面图,如图3(b)所示。从图3(b)中可以看出,系统右侧运动较为杂乱,且Poincare截面图中的点也变得散乱。计算其对应的最大Lyapunov指数λ≈0.007>0,可判定此条件下系统右侧作混沌运动。 (b) f=5.6—— 右侧相图;· Poincare截面图图 3 系统(2)右侧相图及Poincare截面图Fig.3 Phase diagram poincare cross-section diagram on the right side of system 为了进一步验证上述结果的有效性,图4给出了系统(2)右侧位移u随参数f变化的分岔图。可以看出:当参数f=3.5时,系统并没有产生混沌;随着f的增大,系统右侧经历倍周期级联,最终产生局部混沌。同时可以看出,当f=5.6时,系统有局部混沌现象的产生。与前面结果的吻合,进一步验证了Melnikov方法的有效性。 图 4 位移u随参数f变化的分岔图Fig.4 Bifurcation diagram of displacement u with parameter f 固定系统参数k=2.0、ω=1.1、α=2.0、r0=2.0、γ=0.1、ε=0.1,讨论非光滑同宿分叉与光滑同宿分叉同时存在时系统的混沌运动。给式(15)、(21)取等号,分别作出系统(2)右侧非光滑同宿轨与左侧光滑同宿轨中临界值εf随着μ变化的Melnikov临界线,如图5所示。 图 5 系统(2)非光滑同宿轨与光滑同宿轨 的Melnikov临界线Fig.5 Melnikov critical line of non-smooth homoclinicorbit and smooth homoclini- corbit of the system (2) 图5中,线下为非混沌区域,线上可能为混沌区域。从图5可以看出,随着μ的增大,εf也在不断增大。从能量的角度看,因为μ越大,系统阻尼越大,要使系统产生混沌,需要的外激励就越大,所以f就越大。取μ=0.1,系统非光滑同宿轨对应的临界值εf≈0.167,光滑同宿轨对应的临界值εf≈-0.177 1。在图5中取点A(0.1,0.15),使得-0.177 1<εf=0.15<0.167。取μ=1.5,光滑同宿轨对应的临界值εf≈0.949 8,非光滑同宿轨对应的临界值εf≈0.295 6。在图5中取B(1.5,0.8),使得0.295 6<εf=0.8<0.949 8;取点D(1.5,1.0),使得f=1.0>0.949 8。取μ=0.8,系统光滑同宿轨对应的临界值εf≈0.386 4,非光滑同宿轨对应的临界值εf≈0.231 3。在图5中取点C(0.8,0.08),使得εf=0.08<0.231 3<0.386 4。 图5中A(0.1,0.15)点所在的区域是非光滑同宿轨与光滑同宿轨所对应的Melnikov临界线的交叉区域。对于系统左侧来说是可能的混沌区域,对于右侧来说是非混沌区域。为了验证图5所示结果的正确性,分别做出A点所对应的参数下,系统(2)的仿真结果,如图6所示。由图6(a) 可以看出,在A点对应的参数下系统左侧运动比较杂乱,且Poincare截面图中的点也比较散乱,并计算其对应的最大Lyapunov指数λ≈0.001>0 ,那么可知当前参数下系统光滑同宿轨发生分叉。 同样由图6(b)可以看出,在A点对应的参数下系统右侧运动较为规则且Poincare截面图只有3个点,可以得到此条件下系统右侧作周期为3的非混沌运动,与图6所示结果吻合。 (a) 光滑同宿轨 (b) 非光滑同宿轨—— 相图;· 截面图图 6 A点对应参数下系统(2)的相图及 Poincare截面图Fig.6 Phase diagram and Poincare section of system (2) under the parameter corresponding to point A 同样,图5中B(1.5,0.8)点所在的区域是非光滑同宿轨与光滑同宿轨所对应的Melnikov临界线的交叉区域。对于系统左侧来说是非混沌区域,对于右侧来说是可能的混沌区域。图7给出了B(1.5,0.8)点在所对应的参数下,系统(2)的仿真结果。 由图7(a)可以看出,在B点对应的参数下系统左侧运动是非常规则的,且Poincare截面图只有2个点,验证了此条件下系统左侧作周期为2的非混沌运动。同样由图7(b)可以看出,在B点对应的参数下系统右侧运动较为混乱,Poincare截面图中的点也是混乱的,且计算其对应的最大Lyapunov指数λ≈0.06>0 ,进一步验证了此条件下系统右侧作混沌运动,与图5所示结果吻合。 由图7(b)可以看出:在B点对应的参数下系统右侧运动较为混乱,Poincare截面图中的点也是混乱的。计算其对应的最大Lyapunov指数λ,得λ≈0.06>0,进一步验证了此条件下系统右侧作混沌运动。由图7(a)可以看出:在B点对应的参数下系统左侧运动是非常规则的,且Poincare截面图只有2个点。验证了此条件下系统左侧作周期为2的非混沌运动,与图5所示结果相吻合。 (a)光滑同宿轨 (b) 非光滑同宿轨—— 相图;· 截面图图 7 B点对应参数下系统(2)的相图 及Poincare截面图Fig.7 Phase diagram and Poincare section of system (2) under the parameter corresponding to point B 由图5可以看出,点C(0.8,0.08)所在区域为系统左右两侧公共的非混沌区域,点D(1.5,1.0)所在区域为系统左右两侧公共的可能混沌区域。为了验证图5所示结果的准确性,同样分别作出点C和点D对应的参数条件下系统左右两侧的相图和Poincare截面图,如图8所示。由图8(a)可以看出,在C点的参数条件下,系统左右两侧运动都是非常规则的,且Poincare截面图都只有1个点。因此,在此条件下系统左右两侧都作周期为1的非混沌运动。由图8(b)可以看出,在点D的参数条件下,系统左右两侧运动都很杂乱,且Poincare截面图的点也是非常混乱的。在此条件下系统左右两侧都作混沌运动,并且最终诱导系统混沌激变的发生,与图5所示结果相吻合。 (a) C点对应的参数条件 (b) D点对应的参数条件—— 相图;· 截面图图 8 系统(2)的相图及Poincare截面图Fig.8 Phase diagram Poincare cross-section diagram of system 研究了具有非对称结构的形状记忆合金梁模型的混沌运动,分别推导出该系统光滑同宿分叉与非光滑同宿分叉出现Smale马蹄混沌的必要条件,并通过Poincare截面图、相图及最大Lyapunov指数进行了验证分析。结果表明:临界值之下的区域,系统为非混沌状态,临界值之上系统逐渐进入混沌状态,证实了Melnikov方法对于该系统的有效性和普适性。研究还表明:h越大,系统右侧越容易产生混沌; 谐和激励幅值的增大有利于促进系统左右两侧产生局部小混沌,并最终导致混沌的合并。本文的研究推广了Melnikov方法在碰撞振动系统中的应用,研究结果也可用与工程中形状记忆合金梁模型的混沌控制。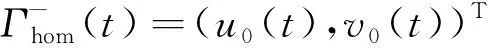
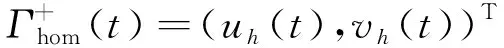

3 Melnikov函数与混沌运动
3.1 非光滑同宿轨 的Melnikov函数
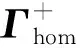
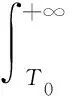
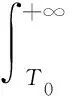
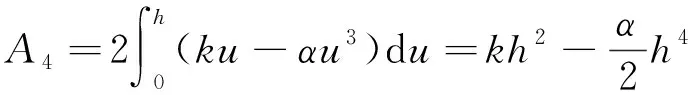
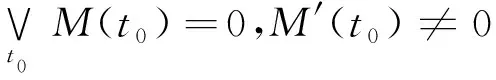
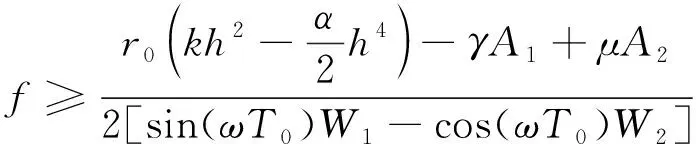
3.2 光滑同宿轨 的Melnikov函数
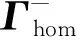
4 数值仿真
4.1 非光滑同宿轨


4.2 系统复杂的混沌运动
5 结 语
