基于Wirtinger型积分不等式的线性时滞广义系统稳定性准则

朱金梁，王 婷，李 涛

(1.南京林业大学 信息科学技术学院，南京 210037；2.南京航空航天大学 自动化学院，南京 211106)

相较于常规系统，广义系统的形式和范畴更具代表性，能够更有效地描述实际系统中各个状态变量之间的关系，因此在机器人系统、金融系统、化工以及通讯等领域应用广泛.同时，实际系统中的时滞现象不可避免且会降低系统性能，甚至导致系统不稳定.因此，研究时滞广义系统的稳定性具有重要理论意义和应用前景.

目前，时滞系统稳定性的研究多基于Lyapunov稳定性定理的时域分析法，该方法主要利用时滞信息进行有效泛函构造并估计其上界，进而获得判定系统稳定的充分条件.如何获得尽可能大的时滞容许上界是当前时滞系统稳定性研究的热点之一[1]，因此，许多学者提出Wirtinger型等积分不等式法[2-5]、凸组合技术[6-7]、自由权矩阵[8-10]和时滞区间分割法[11-12]等研究方法以充分降低结论的保守性.其中，针对时滞广义系统稳定性，基于线性矩阵不等式得到了相应的时滞相关稳定性准则[13-20].虽然时滞广义系统稳定性已得到广泛深入的研究，但是尚未出现将时滞分割技术和新型积分不等式相结合以降低保守性的研究成果.对此，本文首先将时滞分成两个子区间并构造多重积分下的Lyapunov泛函；然后借助Wirtinger型积分不等式估计泛函导函数更紧上界，获得易于验证且保守性较小的稳定性准则；最后借助数值算例证明方法的有效性.

1 系统和问题描述

考虑如下线性时滞广义系统

(1)

式中：x(t)∈Rn为系统(1)的状态；Rn为全体n维实数向量集合；t为时间；τ≥0为系统状态时滞；E,A,Ad∈Rn×n为已知常数矩阵，且rank(E)=r≤n；φ(t)为系统(1)的初始状态.

定义1[13]如果|sE-A|不恒为0，则(E,A)是正则的，如果deg(|sE-A|)=rank(E)，则(E,A)是无脉冲的.其中，deg(·)为行列式的最高阶数.

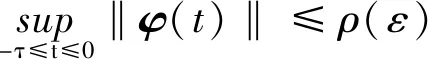
为了便于建立主要结论，需要给出如下3个重要引理.

引理1[5]给定正定矩阵R，连续可微函数x(·)：[a,b]→Rn，则有

其中:

引理2[5]给定正定矩阵R，连续可微函数x(·)：[a,b]→Rn，则有

其中:

Ω1=x(b)-x(a)

引理3[5]给定正定矩阵R，连续可微函数x(·)：[a,b]→Rn，则有

其中:

2 渐近稳定性准则

为了简化证明过程，给出如下记号：

K1=Ae1+Ade3

K4=τe4-4e6

K6=τe5-4e7

K8=e2-e3

K9=e2+e3-4e4

K11=e1-e2

K12=e1+e2-4e5

K14=e3-2e4

K16=e2-2e4

K18=e1-2e5

定理1给定τ>0，如果存在适当正定矩阵P,Q1,Q2,Ri(i=1，2,3，4),Si(i=1，2，3)和常数矩阵Z使得下式中的LMI(Λ负定)成立，则系统(1)渐近稳定，其中

(2)

证明基于时滞分割区间构造如下多重积分Lyapunov-Krasovskii泛函

V(x(t),t)=ηT(t)Pη(t)+

(3)

式中：

分别引入如下增广向量和向量记号：

沿着系统(1)对泛函V(x(t),t)关于t求导

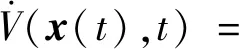
(4)

首先，利用引理1，对式(4)中的第1和2积分项进行估计

(5)

式中：

T1=τμ1(t),T2=τμ1(t)-4μ3(t)

T3=τμ1(t)-12μ3(t)+48τ-1μ5(t)

T4=τμ2(t),T5=τμ2(t)-4μ4(t)

T6=τμ2(t)-12μ4(t)+48τ-1μ6(t)

其次，利用引理2，对式(4)中的第3和4积分项进行估计

(6)

式中：

U1=x(t-0.5τ)-x(t-τ)

U2=x(t-0.5τ)+x(t-τ)-4μ1(t)

U3=U1+12μ1(t)-48τ-1μ3(t)

U4=x(t)-x(t-0.5τ)

U5=x(t)+x(t-0.5τ)-4μ2(t)

U6=U4+12μ2(t)-48τ-1μ4(t)

最后，利用引理3，对式(4)中第5～7积分项进行估计

(7)

式中：

V1=x(t-τ)-2μ1(t)

V2=x(t-τ)-8μ1(t)+24τ-1μ3(t)

V3=x(t-0.5τ)-2μ1(t)

V4=x(t-0.5τ)+4μ1(t)-24τ-1μ3(t)

V5=x(t)-2μ2(t)

V6=x(t)+4μ2(t)-24τ-1μ4(t)

根据系统(1)和ETL=0，有

2xT(t)ZLT(Ax(t)+Adx(t-τ))

(8)

(9)

当E为单位矩阵时，即rank(E)=n，则系统(1)由线性退化为常规时滞线性系统.基于定理1的证明过程，可以进一步得到如下推论.

推论1给定τ>0，如果存在适当正定矩阵P,Q1,Q2,Ri(i=1，2，3，4),Si(i=1，2，3)和常数矩阵Z使得下式中的LMI(Λ负定)成立，则系统(1)渐近稳定，其中

(10)

证明当E为单位矩阵时，根据定理1的证明方法并设定E=In(In为n×n维单位矩阵)，可直接获得该推论，证明过程不再赘述.

根据获得的定理1和推论1可知，将时滞分割法用于泛函构造中能够充分利用分割后各时滞子区间的信息.同时，利用Wirtinger型积分不等式估计出泛函导函数更紧上界，能够考虑到现有研究忽略的信息，因此本文方法的适用范围更大.

3 数值算例

例1为了说明定理1具有较小的保守性，考虑文献[15-17]使用的算例，系统参数为

因为Ad中包含未知参数c，所以在求解定理1中的LMI时，需要提前设定c的取值.基于设定的不同c值，利用MATLAB的LMI工具箱对式(2)中的LMI进行求解以获得相应的最大时滞容许上界(τmax).同时，与文献[15-17]中的计算结果进行比较，结果如表1所示，其中N为时滞分割的区间数.由表1可知，τmax随c值的增加而减小；与文献[15-17]中的结果相比，定理1中的τmax值均较大，系统的适用范围更广，因此其具有较小保守性.此外，在c=1.2和τ=9.219 8的情况下，对系统状态进行仿真，结果如图1所示.图1中系统状态变量x1和x2渐近稳定，证明了定理1的有效性.

表1 不同c值下的最大时滞容许上界值Tab.1 Maximum allowable upper bounds on time-delay at different values of c

图1 系统状态x1和x2的响应曲线Fig.1 Response curves of system in states x1 and x2

例2根据文献[18]，对倒立摆的直流电机控制系统进行建模，获得如下系统参数：

由上述参数可知，该系统为广义系统.根据定理1并取τ=9.800 0，利用MATLAB的LMI工具箱对式(2)中的LMI进行求解，并验证该LMI存在可行解.设定合适的初始状态并利用MATLAB中的Simulink获得系统仿真曲线(见图2).图2中系统状态变量x1,x2和x3在t=2.6 s时达到稳定，说明了该方法具有一定的应用前景.

图2 系统状态x1～x3的响应曲线Fig.2 Response curves of system in states x1-x3

例3考虑具有如下参数的时滞线性系统：

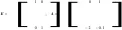
由上述参数可知，该系统为常规时滞系统，因此可以借助推论1判定系统的稳定性.利用MATLAB的LMI工具箱对式(10)中的LMI进行求解，在存在可行解的前提下获得的最大时滞容许上界为 2.898 5，同时将推论1与文献[4,19,20]中的结果进行比较，结果如表2所示.与现有方法相比，推论1的τmax值均较大，其具有较小保守性.

表2 最大时滞容许上界值Tab.2 Maximum allowable upper bounds on time-delay

4 结语

针对时滞线性广义系统渐近稳定性问题，利用新型时滞分割技术并提出多重积分下的Lyapunov泛函构造.同时，借助Wirtinger型积分不等式估计出泛函导函数中积分项更小上界，并充分考虑现有研究忽略的信息，进而基于LMI建立确保系统渐近稳定且保守性较小的充分条件.最后通过3个数值算例说明了方法的有效性和先进性.