非仿射纯反馈非线性切换系统自适应控制

陈龙胜，王 琦，何国毅

(南昌航空大学 飞行器工程学院，南昌 330063)

切换系统是一种应用广泛的特殊混杂系统，具有明确的工程背景和广泛的应用前景.不确定非线性切换系统的控制和稳定性问题是当前研究的热点.近年来，学者们热衷于利用通用逼近器和反演法解决含未知非线性函数的不确定非线性切换系统自适应控制问题，并采用共同Lyapunov函数和平均/最小驻留时间以及多Lyapunov函数法分析闭环系统的稳定性.司文杰等[1-3]基于共同Lyapunov函数为一类非线性切换系统设计了自适应神经网络/模糊控制器.Zhai等[4-5]在满足平均/最小驻留时间的前提下，为一类非线性切换系统设计了自适应模糊控制器.Long等[6-7]采用模糊系统逼近系统中的未知非线性函数，并基于多Lyapunov函数分析法为一类非线性切换系统设计了自适应切换控制器.但是，这些基于反演法的设计控制策略存在“微分爆炸”问题.Swaroop等[8]首次通过引入一阶低通滤波器，即动态面控制(Dynamic Surface Control,DSC) 技术解决 “微分爆炸”问题.然后，一些针对非线性切换系统的DSC控制策略相继被提出.Zhai等[9]利用模糊逻辑逼近系统的未知不确定非线性特性，并在满足平均/最小驻留时间的前提下为一类非线性切换系统设计了自适应DSC控制器.Zhai等[10]基于共同Lyapunov函数为非线性切换系统设计了自适应模糊DSC控制器.尽管DSC控制技术已被应用于非线性切换系统，但大多数研究仍针对严反馈型非线性系统，目前关于非仿射纯反馈非线性切换系统的DCS控制研究成果较少.

针对一类结构和参数均未知的非仿射纯反馈非线性切换系统，设计在任意切换下的自适应跟踪控制器.在控制器的设计中，利用径向基函数神经网络(Radial Basis Function Neural Network,RBFNN)和Nussbaum函数处理未知非线性动态问题，且RBFNN采用单一自适应更新率.所设计的控制器既可以满足系统非线性特性和控制方向未知以及系统切换的需求，又可以避免神经网络径向基函数的大量运算.引入低通滤波器解决反演设计的“微分爆炸”问题，从而进一步减少计算负荷.此外，基于共同Lyapunov函数设计状态反馈控制器并分析闭环系统的稳定性，避免了切换发生时控制参数跳变和调节参数过多的问题.

1 问题描述及预备知识

1.1 问题描述

考虑如下非仿射纯反馈非线性切换系统：

(1)

(2)

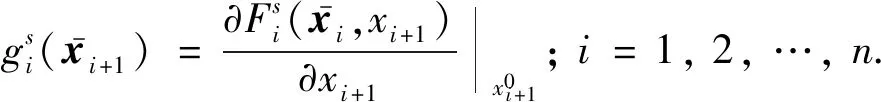
控制目标：在任意切换模式下，通过设计自适应控制器使得系统的输出能够跟踪期望轨迹yr(t)，且保证闭环系统所有的信号有界.为便于控制器设计，引入如下假设、定义和引理.

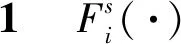
其中：i=1,2,…,n.

假设2[11]yr(t)光滑有界且具有二阶连续有界导数，即存在常数B0>0使得

定义1[12]如果连续函数N(χ):R→R满足

(3)

则称N(χ)为Nussbaum函数.本文采用的Nussbaum函数为N(χ)=χ2cosχ.

引理2[13]设V(·)和χj(·) (j=1,2,…,m)是定义在[0,tf)上的光滑函数,且满足∀t∈[0,tf),V(t)≥0.N(χj)为一个光滑的Nussbaum函数,对∀t∈[0,tf),若存在

(4)

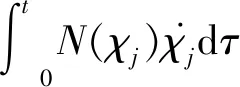
引理3[14]对于tf>0,若闭环系统的解在[0,tf)内有界,则tf=∞.

引理4(杨氏不等式)[11]对任意的(a,b)∈R2，如果实数γ,c,d且满足h>0,c>1,d>1,(c-1)(d-1)=1，那么

(5)

1.2 RBFNN

RBFNN在控制器的设计过程中被广泛用于逼近系统的未知非线性函数.设存在连续函数F(Z):Rp→R，在紧集ΩZ∈Rp和任意值ε>0的条件下，有神经网络ϑTψ(Z)使得Sup|F(Z)-ϑTψ(Z)|≤ε，其中ϑ∈R为神经网络的权值，>0为神经网络隐含层节点数.Z∈Rp为神经网络输入，ψ(Z)=为径向基函数.基于神经网络的任意逼近原理，F(Z)可被逼近为

F(Z)=ϑ*Tψ(Z)+ε(Z)

(6)

式中：ε(Z)为逼近误差；ϑ*为理想权值向量，且

(7)

2 控制器设计及稳定性分析

基于RBFNN和Nussbaum函数为系统设计自适应反演切换控制器，并基于共同Lyapunov函数分析闭环系统的稳定性.

2.1 控制器设计

根据式(2)和RBFNN可进一步将系统(1)描述为

(8)

(9)

式中：i=1,2,…,n；b>0为待设计的参数.

为进行反演设计，通常需定义如下的坐标变换

(10)

(11)

(12)

(13)

式中：i=1,2,…,n-1；μi>0为时间常数.

根据定义的坐标变换，可为系统(1)设计如下控制律

(14)

式中：i=1,2,…,n-1；κi>0,γi>0为设计常数.其参数调节律为

(15)

式中：i=1,2,…,n；π>0,λ>0为设计常数.

2.2 稳定性分析

为了对由控制律和参数调节律组成的闭环系统进行稳定性分析，提出如下定理.

定理考虑系统(1)，在满足假设1和2的前提下，采用控制律式(14)和参数调节律式 (15)，则可保证闭环系统所有信号半全局一致有界，且通过调整控制器参数使跟踪误差可收敛到原点的一个较小邻域.

(16)

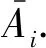
根据式(8)、(10)和 (11)可得

(17)

选取Lyapunov函数

(18)

则其对时间的导数为

(19)

将式(10)～(11)和 (14)～(17)代入式(19)可得

(20)

根据杨氏不等式、式(9)和假设2可得

(21)

(22)

(23)

(24)

(25)

(26)

(27)

式中：

(i=2,…,n-1);

式(27)两边同乘eC t可得

(28)

式(28)两边在[0,t]内的积分为

(29)

则有

(30)

根据式(18)和 (30)进一步可得

(31)

3 仿真试验

考虑如下的结构和参数均未知的非仿射纯反馈非线性切换系统

(32)

图1 切换信号Fig.1 Switching signal

由图2可知，系统的实际输出能够很好地跟踪期望轨迹.由图3可知，系统的跟踪误差能够很快地收敛到原点的一个较小邻域.由图4可知，所有的自适应参数最终均能够较快地收敛到常值附近.仿真结果表明：该控制器具有良好的跟踪性能和稳定性.

图2 系统输出与期望轨迹Fig.2 System output and desired trajectory

图3 跟踪误差曲线Fig.3 Tracking error

图4 参数自适应更新率Fig.4 Update laws of parameters

4 结语

非线性切换系统是控制理论和工程领域的研究热点.针对一类更具代表性的结构和参数均未知的非仿射纯反馈非线性切换系统，利用中值定理将其等价转化为类似严反馈形式的非线性系统.在此基础上，利用RBFNN在线逼近系统的未知非线性函数，并利用Nussbaum 增益技术和低通滤波器分别解决系统控制增益未知的问题和反演设计的“微分爆炸”问题.最后，基于共同Lyapunov函数为系统设计状态反馈控制器.所设计的控制器不依赖系统的具体模型，避免了切换发生时控制参数跳变和调节参数过多的问题，减少了计算负荷.