舰载机无杆式牵引车横摆稳定性控制
2020-10-12戚基艳金嘉琦付景顺
戚基艳,金嘉琦,付景顺
(沈阳工业大学 机械工程学院,沈阳 110870)
牵引车作为舰基保障的一种新型设备,在现代舰载机调运中获得了广泛使用[1],直接影响着舰载机的调运安全与效率[2-3].现行飞机牵引车向着小型化和智能化的趋势发展[4],解决了传统牵引车的诸多缺点,提高了牵引车的稳定性与调运效率.无杆式牵引车能够更好地融合先进设计技术,操纵稳定性及灵活性更高,是未来舰载机牵引车发展的趋势[1,4].由于舰载机牵引车在相对狭窄的甲板上进行作业运动,且船体受海浪运动对牵引车产生复杂的耦合影响,极易出现失稳的情况[5].由于横摆稳定性能的优劣直接影响到牵引车的安全性和操稳性,所以讨论舰载机无杆式牵引车(下文简称舰载机牵引车)的横摆稳定性对于舰载机在甲板上调运作业的效率和安全性都有着重要的意义.
目前,对于舰载机牵引车的行驶稳定性研究主要是基于一定的算法进行路径跟踪规划,从而保证牵引运动的安全性和高效性[2,3,6],但该种规划没有考虑牵引车自身的运动特性对牵引运动的影响.对于牵引运动的研究大多以陆地环境为背景,没有考虑复杂的舰载情况[7],对于舰载机牵引车的侧向运行特征,鲜有文献研究.
本文选取一款遥控舰载机牵引车,由轮毂电机提供驱动力(后驱),提高了控制的自由度和精确度[8].考虑舰船3自由度耦合运动影响,提出将被牵引的舰载机简化为两轮模型,再以外力形式加载于牵引车,建立目标舰载机牵引车的时变非线性2自由度横摆动力学模型.针对目标牵引车的时变非线性特性,采用模糊自适应比例积分微分(PID)控制和滑模变结构控制设计了两种控制器.通过仿真分析不同海况下舰载机牵引车的横摆角速度,证明了所设计的滑模变结构控制器能够很好地应对舰载的外界环境,具有适应性强、响应速度快、稳健性高等优点,能够较好地控制舰载机牵引车的横摆稳定性,为进一步研究舰载机牵引车的行驶稳定性奠定了实验和理论基础.
1 牵引车动力学模型分析
1.1 舰船运动分析
舰船在海洋上行驶时,可以看作是产生6个自由度耦合运动的刚体,分别为横摇、纵摇、艏摇、垂荡、横档和纵荡.其中,横摇、纵摇、垂荡运动对船体的影响最大,其危害也是最大的[9].理想条件下,假设舰船相对于质心运动,可将舰船运动与欧拉角结合,采用简化的舰船运动模型表示舰船的横摇θ、纵摇β和垂荡z运动特性:
(1)
1.2 牵引系统坐标系
舰载机牵引车的系统动力学模型如图1所示,系统坐标系遵循右手笛卡尔法则,各坐标系原点均为各自的质心.其中:On-xnynzn为地理惯性坐标系;Oj-xjyjzj为舰船质心坐标系;Oi-xiyizi(i=1,2)分别为牵引车和舰载机的连体坐标系;Ri(i=1,2)分别为牵引车和舰载机的质心在惯性坐标系内的位矢;ri(i=1,2)为牵引车和舰载机的质心在舰船坐标系内的位矢;Rn为舰船质心在惯性坐标系内的位矢;εi(i=1,2)为牵引车和舰载机相对于船体坐标系的横摆角;Fy1为牵引车两个前轮的侧向合力;Fy2为牵引车两个后轮的侧向合力;Fy3为舰载机两个后轮的侧向合力;l1、l2、l5分别为牵引车前轴、后轴和铰接点距其质心的距离;l3、l4分别为舰载机前轮、后轴距其质心的距离;δf为前轮转向角.
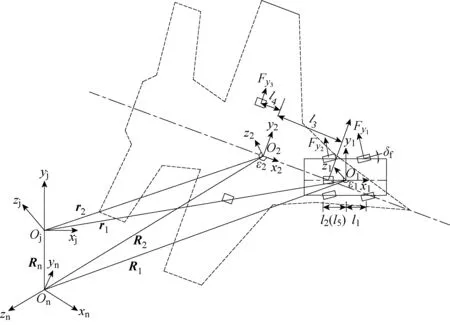
图1 舰载机牵引车系统模型Fig.1 Carrier-based aircraft tractor traction system model
(4)
由于舰船的横摇角|β|<π/4始终成立,所以该矩阵不存在奇异(β=π/2时为奇异矩阵),不影响后续的运动学分析.
由于舰船的甲板面比较平坦,目标牵引车由轮毂电机驱动且车身低矮,轮毂电机内悬架带来的平顺性影响较小,所以在舰载机牵引车系统的行驶分析中不考虑其相对甲板的俯仰、侧倾以及垂向自由度.则船体坐标系到连体坐标系的转换关系可以表示为[1]
(7)
1.3 舰载机牵引车运动学和动力学分析
假设牵引车和舰载机的纵向速度相等,舰载机和牵引车在甲板上相对于惯性坐标系的运动(绝对运动)等于舰船相对于惯性坐标系的运动(牵连运动)与舰载机和牵引车相对于舰船运动(相对运动)之和,则有
Ri=ri+Rn
(8)
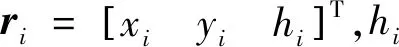
结合式(2)~(8),可得:
(11)
(12)
目标牵引车由轮毂电机驱动,由簧载质量引起的侧倾运动较小,可参考汽车2自由度操纵模型及其假设.假设牵引车在舰船甲板面上牵引舰载机作匀速直线运动,纵向合力为0,可以忽略作用于单个车轮的回正力矩,对于舰船的分析主要考虑对其影响较大的运动.结合式(4)和(7),目标牵引车和舰载机在惯性坐标系下的横摆角加速度可表示为
(13)
目标牵引车在惯性坐标系下的侧向和横摆运动方程为
(14)
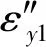
(15)
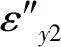
借鉴汽车2自由度牛顿矢量法和基本操纵模型建立方法,结合式(11)和(12),可得舰载机牵引车系统动力学模型为
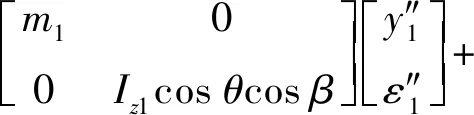
(16)
式中:Cα1和Cα2分别为牵引车特定载荷下前轮和后轮的侧偏刚度,当牵引车前轮侧偏角α较小时,该值与前轮侧偏角呈正比例关系;uc为牵引车和舰载机的恒定前进速度.式(15)的方程组可以整理成矩阵的形式
AX″(t)+BX′(t)+HX(t)=F(t)
(17)
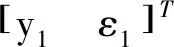
2 牵引车横向稳定性控制器设计
横摆力矩控制系统是汽车主动安全控制的重要组成部分,同时也是提升汽车操纵稳定性最有效的技术途径之一.轮毂电机驱动为车辆利用直接横摆力矩控制实现操纵稳定性控制提供了有利的硬件基础[8].本文的控制目标是通过施加补偿横摆力矩来实现舰载机牵引车的横摆稳定性控制,考虑到目标牵引车低速行驶的工况、舰船甲板面上的附着系数不确定等外界因素的影响[6],输入控制变量选择牵引车相对于舰船坐标系的横摆角速度.目标牵引车横摆运动是典型的复杂时变非线性问题,受海洋环境等未知外在扰动,因此选择对精确数学模型依赖不大、对参数不确定性抗干扰性较强、物理实现较为简单的滑模变结构控制[12]和模糊自适应PID两种控制算法[13]抑制牵引车的横向失稳.通过仿真对比分析,选择出适应舰载环境、响应时间短、稳健性更好的控制方法.
2.1 参考模型与控制变量
确认参考模型和选择控制变量是控制设计的首要任务.通过保持对参考模型理想横摆角速度的跟随,使轮胎始终处于良好的线性范围内,能够抑制目标牵引车的横向失稳.采用稳健性更好的零化质心侧偏角的直接横摆力矩控制参考模型[14].后轮驱动的目标牵引车期望横摆角速度公式为
(18)
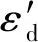
2.2 滑模变结构控制器设计
通过滑模控制器计算车辆按照理想状态行驶所需的补偿横摆力矩,从而实现对理想横摆角速度的跟随.以ε1与横摆角度的理想值εd的误差为控制变量,定义滑模面的控制切换函数为
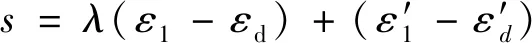
(19)
式中:λ为权值且必须满足Hurwitz条件,即λ>0.
根据式(15)、(17)和(18),同时考虑补偿横摆力矩ΔMz的作用可得
(20)
滑模控制率选用指数趋近律进行设计,则有
s′=-k1sgn(s)-k2s
(21)
式中:k1为等速趋近项待定参数,决定了系统的抖动程度,当s趋近于0时,趋近速度为k1,而不为0,可以保证系统状态能够在有限的时间内到达滑膜面[12];k2为指数趋近项待定参数,表征系统到达滑模面的时间,保证当s较大时,系统能以较大的速度趋近于滑动模态.为了保证控制系统在受到外界干扰后能在有限的时间内稳定在滑模面上,k1和k2必须大于0[12],且为了保证快速趋近的同时削弱抖振,应在增大k2的同时减小k1.
根据式(19)和(20),可获得维持牵引车横向稳定所需的补偿横摆力矩ΔMz为
ΔMz=-Iz1cosθcosβ[k1sgn (s)+k2s+
(22)
根据“准滑动模态”和“边界层”控制方法,用稳健性较好的饱和函数sat(s/φ)(φ为边界层阈值)替代控制律中的符号函数sgn(s),能够实现准滑动模态控制,即在边界层以外采用正常的滑模控制,在边界层内为连续状态的反馈控制,保证在滑模面附近控制输入的光滑连续性[12,15].边界层厚度与控制效果和抖振程度呈反向变化,厚度越小,控制效果越好,抖振程度越强,因此需要折中考虑,经过后期多次仿真实验,边界层φ最终取值为0.05.
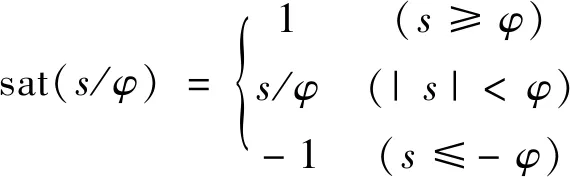
(23)
利用李雅普诺夫第二稳定性判据对所设计的系统进行稳定性分析,定义李雅普诺夫函数为
(24)
将式(18),(19)和(21)代入,可得
-k1|s|-k2s2≤0
(25)
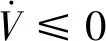
2.3 模糊自适应PID控制器设计
对于目标牵引车的横向稳定性采用模糊自适应PID控制器进行控制,输出参数依然是补偿横摆转矩,输入信号为控制目标值的误差e以及误差变化率ec,可表示为
(26)
选择合适的模糊化和解模糊化方法以及模糊规则,e和ec对PID参数kP(比例系数),kI(积分系数),kD(微分系数)进行自调整,调整后的参数可以表示为
(27)
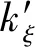
根据系统模型,通过多次仿真实验数据,确定输入变量e和ec的基本论域为[-2,2];输出变量Δkξ的基本论域为[-6,6];输入和输出的模糊集合均为{NB,NM,NS,ZO,PS,PM,PB},其中:NB为负大;NM为负中;NS为负小;ZO为0;PS为正小;PM为正中;PB为正大.打开曲面观测窗口,可以查看Δkξ分别在论域上的输出曲面,如图2所示.通过选取输入量化因子和输出比例因子实现模糊化论域的输入需求和论域解模糊化的输出需求.量化和比例因子的取值主要依据单一控制变量方法,根据文献[13]的经验规则不断进行仿真试凑来确定.采用“Mamdani”型推理,用面积重心法进行去模糊化,最终决策出的补偿横摆力矩可以通过轮毂电机平均分配驱动力的形式实现具体的分配.
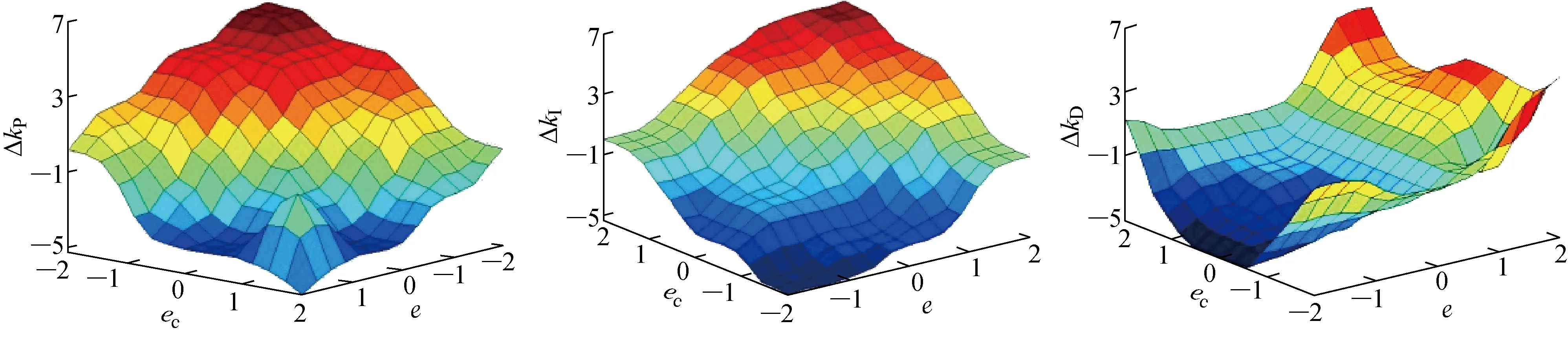
图2 Δkξ论域输出曲面Fig.2 Δkξ output surface on fuzzy domain
3 仿真实验与结果分析
3.1 仿真模型搭建
为验证所设计的牵引车补偿横摆力矩稳定性控制方法的有效性,借助MATLAB/Simulink动态仿真平台,建立包括舰载机牵引车2自由度时变非线性动力学模型[16]在内的横摆稳定性仿真模型,如图3所示;目标牵引车的结构参数如表1所示.其中:Tx为轮毂电机的扭矩;Fx为轮毂电机提供给驱动轮的纵向力.
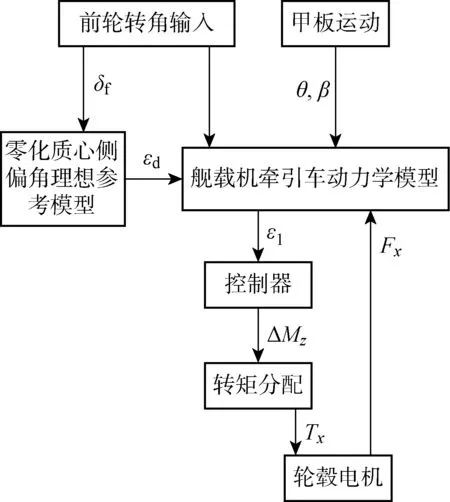
图3 目标牵引车控制仿真模型Fig.3 Simulation model of target tractor control
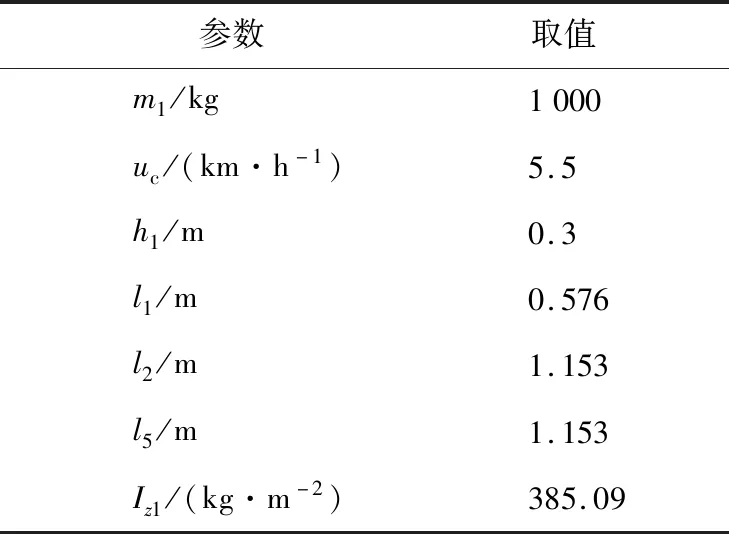
表1 目标牵引车的结构参数Tab.1 Structural parameters of target tractor
牵引车的轮胎侧偏刚度采用文献[17]的实验数据与垂直载荷进行最小二乘法线性拟合获得
Cαζ=2(7.374 1Nζ-2 302)
(28)
式中:Nζ(ζ=1,2)为牵引车牵引工作时,前、后轴的载荷.为了保证牵引车转弯时的准确性,结构设计时将舰载机作用于牵引车的重力作用点与牵引车两后驱动轮的轴线中心点重合,因此舰载机作用于牵引车的质量全部由后轴承担.牵引车牵引舰载机在甲板上作匀速运动,牵引车前轴载荷的分配可以根据静态轴荷分配进一步进行计算获得[8],后轴载荷分配是牵引车自身后轴静态载荷与大约10%的舰载机质量之和[18].
飞机在地面静止时,不会因为侧向风产生侧向移动[19],甲板面相对于路面的摩擦力更大[20],舰载机被牵引匀速行驶,因此可以假设其相对于甲板面没有横向移动.
根据式(13)及文献[1]中对于舰载机牵引车侧偏力的分析可知,当侧偏角在线性范围内且ε1≈ε2的前提下,Fqy的表达式为
(29)
式中:Cα3为舰载机后轮侧偏刚度.根据文献[1],设各参数取值为舰载机质量为25 t,质心高度为2.67 m,舰载机后轴到质心的距离为1.1 m,飞舰载机后轴侧偏刚度为551.272 kN/rad.
3.2 仿真结果与分析
参照汽车前轮转角阶跃输入实验和单一正弦转角输入实验,根据牵引车的实际工况,对牵引车前轮分别施加阶跃输入和正弦输入,分别仿真牵引车在甲板上出现横向滑动工况和小角度转向工况,如图4所示.在初始仿真过程中,航母以10 m/s的速度匀速前进,纵摇运动规律为β=1°sin(0.2t+6°),横摇运动规律为θ=1.5°sin(0.3t+6°),其中t为仿真时间[21].滑模变结构控制器中,相关参数的仿真取值分别为λ=0.5,k1=0.6,k2=12;模糊自适应PID控制器中相关参数的仿真取值分别为kP=25,kI=26,kD=11.
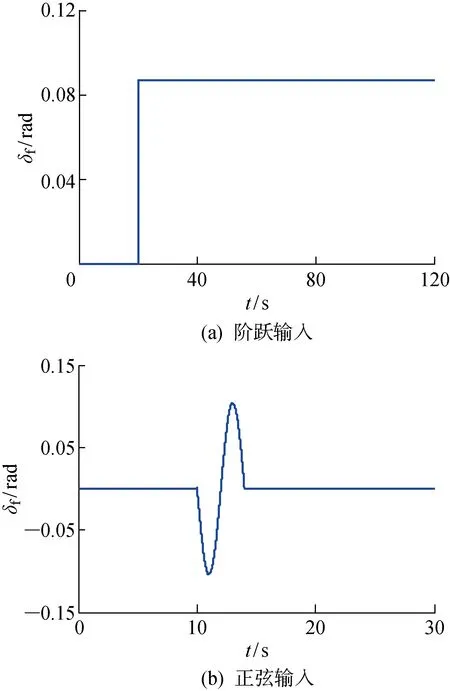
图4 前轮转角输入Fig.4 Input of front wheel angle
验证模糊自适应PID控制器和滑模变结构控制器对目标牵引车横向稳定性控制的有效性.牵引车前轮转角阶跃输入和正弦输入下的两种控制器的仿真结果对比如图5所示.从图5可以看出,滑模变结构控制能够更好地跟随理想值,响应迅速,控制过程精确且稳定.模糊自适应PID控制虽然能够在一定误差范围内保持控制效果,但响应时间长,且控制精度不高.此外在正弦输入下,模糊自适应PID控制的响应时间及适应效果更差.
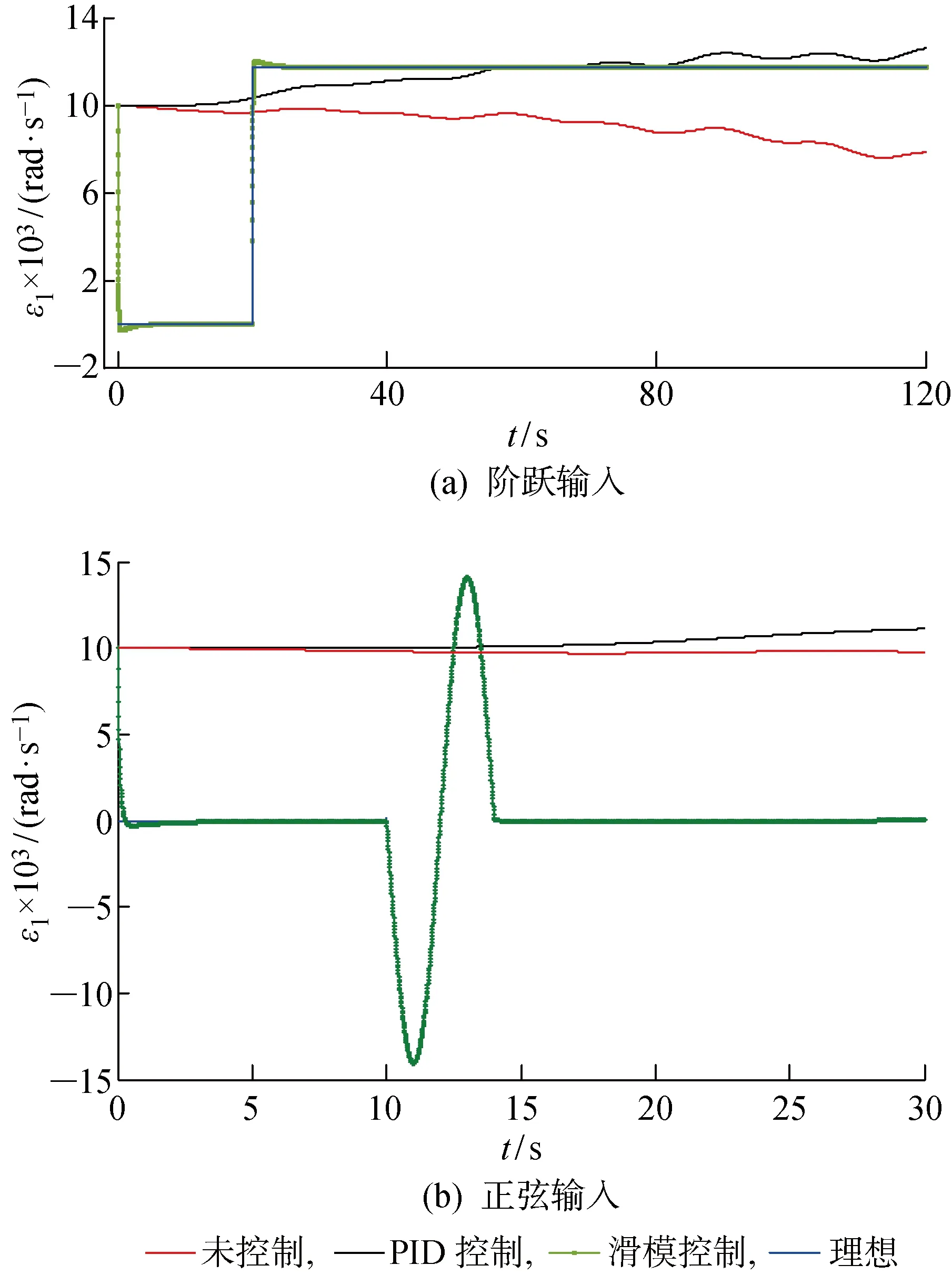
图5 横摆角速度仿真结果对比Fig.5 Comparison of yaw angular velocity simulation results
为了证明不同海况条件下,滑模变结构控制器对抑制目标牵引车横向失稳的效果,即滑模变结构控制器的有效性和稳健性,分别仿真4级和5级海况下控制器的效果,海况数据来源于文献[22].在4级和5级海况下,前轮转角阶跃输入下的滑模变结构控制的横摆角速度输出如图6(a)所示,没有控制器的牵引车横摆角速度输出如图6(b)所示.在4级和5级海况下,前轮转角正弦输入下滑模变结构控制的横摆角速度输出如图7(a)所示,没有控制器的牵引车横摆角速度的输出如图7(b)所示.通过对比仿真实验可知:无论前轮转角为阶跃输入还是正弦输入,滑模控制器都能够在一定范围内对理想横摆角速度进行跟随,均能较好地保证响应时间和控制误差.
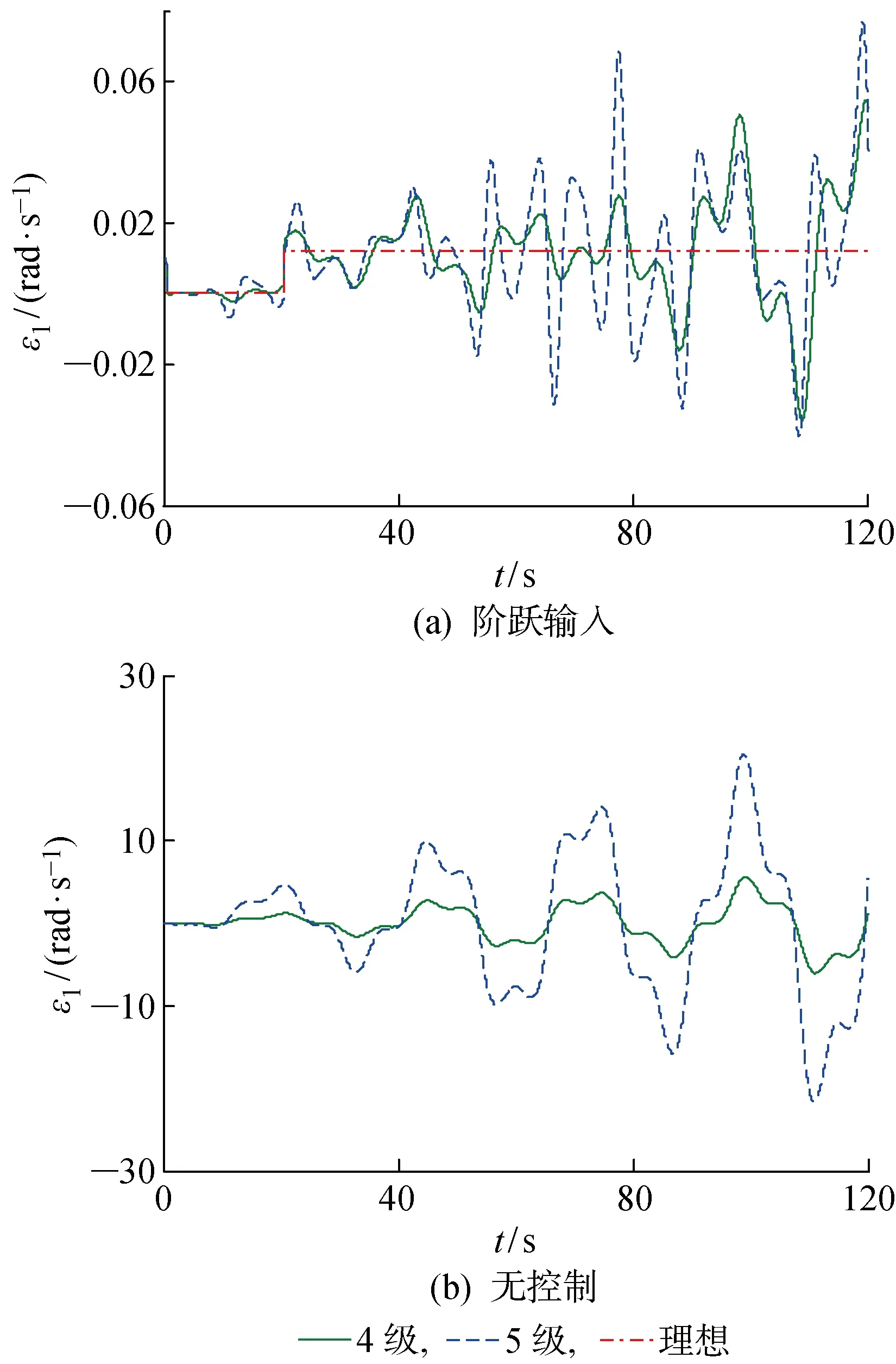
图6 阶跃输入的横摆角速度对比Fig.6 Comparison of yaw rate with step inputs
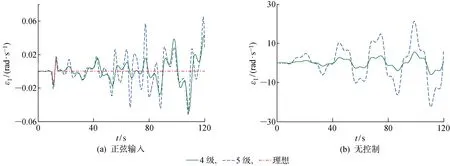
图7 正弦输入的横摆角速度对比Fig.7 Comparison of yaw rates with sine inputs
为了能够进一步验证所设计的滑模控制器对目标牵引车控制的有效性和稳健性,仿真对比了6级海况前轮转角阶跃和正弦输入下,目标牵引车的横摆角速度输出,并将其与图6和7的仿真结果进行对比,如图8所示.由图8可知,设计的滑模控制器虽然能够将目标牵引车的横摆角速度输出控制在一定的范围内,但却与理想值产生了较大的差异.不同等级海况的横摆角速度值统计如表2所示.其中:ε1,max为最大值;ε1,min为最小值.由表2可知,相比4、5级海况,6级海况下目标牵引车的横摆角速度出现了数量级的变化,牵引车的稳定性受到了较大的影响.实际上,美军要求舰载机需要在中等海况下起飞,对比相关文献给出的中等海况标准[23]可知,本文的5级海况下的控制稳健性已经能够满足舰载机的工作环境要求上限.
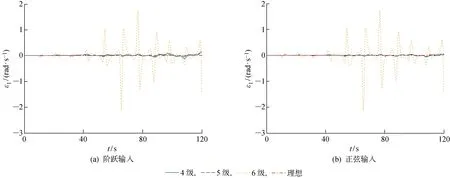
图8 6级海况下横摆角速度对比Fig.8 Comparison of yaw rates at sea level 6

表2 不同等级海况下横摆角速度值统计(rad/s)Tab.2 Statistics of yaw rates in different sea states (rad/s)
4 结语
针对舰载机牵引车运动的复杂性,考虑舰船3自由度耦合作用的影响,舰载机简化为两轮模型,建立了甲板上舰载机牵引车2自由度时变非线性动力学模型.
基于建立的理论模型,考虑牵引车低速且外界环境多输入影响的运行工况,选择了基于准滑动模态的滑模控制和模糊自适应PID两种典型时变非线性系统的控制器进行相关参数设计,通过产生补偿横摆力矩实现对理想横摆角速度的跟随,从而实现抑制牵引车横向失稳的目标.
仿真实验结果表明,模糊自适应PID控制器响应时间长、输出误差范围大,且对输入误差范围和量化因子以及比例因子等参数有较高要求.基于准滑动模态的滑模控制器能够很好地抑制相对横摆角速度的增加,响应迅速且较好地跟踪了期望的理想值.同时,通过仿真舰船在4级、5级和6级海况下的运行环境,验证了基于准滑动模态的滑模控制器对目标牵引车在5级海况及以下能够保持较好地控制效果的结论,表现出较好的稳健性和响应速度,满足目标牵引车的运行工况需求.
