基于变分贝叶斯理论的不确定厚尾噪声滤波方法
2020-10-12董祥祥吕润妍蔡云泽
董祥祥,吕润妍,蔡云泽
(上海交通大学 自动化系;系统控制与信息处理教育部重点实验室;海洋智能装备与系统集成技术教育部实验室,上海 200240)
卡尔曼滤波及其改进算法由于滤波性能良好而应用广泛[1-3],其效果主要取决于噪声统计的先验特性,且受限于正态分布的量测噪声统计[4].在进行目标跟踪时,传感器的不可靠因素常诱导出量测野值,导致离均值较远处的量测噪声的不确定性增大,呈现 “厚尾特性”[5].而传统的卡尔曼滤波及其改进算法使用标准高斯分布,无法准确描述实际的厚尾噪声,存在估计误差过大的问题.对此,学者们进行了大量研究,提出了广义最大似然估计法[6]、多模型方法[7]和自适应联合估计算法[8].
广义最大似然估计方法利用量测中的高阶统计信息对状态进行估计,相比于卡尔曼滤波使用的二阶统计信息,其可提高量测非高斯条件下的状态估计精度,但该方法没有考虑量测噪声的厚尾特性,从而忽略了部分先验信息,限制了状态估计精度的提高[9].多模型方法利用不同模式的有限高斯分布之和对特殊形式的非高斯厚尾噪声进行建模,进而通过加权高斯和计算状态后验概率密度函数,但该方法受限于模型集的选择方式和模型数量[10].基于自适应联合估计的期望最大化方法利用E-Step和M-Step步骤对目标状态和隐变量进行辨识和估计[11],但其估计效果受隐变量维数的影响较大,不利于期望极大化估计[12].
针对以上问题,Piché等[13]采用多变量Student’s t分布对厚尾噪声进行建模,并利用变分贝叶斯理论求解状态的后验分布.但该方法假设Student’s t分布的尺度矩阵和自由度参数固定不变,令算法不能自适应调整量测噪声的统计特性,易降低滤波器性能.Yun等[14]提出利用Pearson Type VII 分布描述厚尾噪声,并据此描述包含在正常量测噪声中的随机离群厚尾噪声.在测量建模中引入遵循β-Bernoulli 分布的判断因子,利用变分贝叶斯理论实现状态的自适应鲁棒估计.Pearson Type VII 分布不受“双自由度参数必须相等”的约束,因此对随机厚尾噪声的适应性更强,在厚尾噪声估计中具有更好的鲁棒性[15].
为了解决在尺度矩阵和自由度参数固定不变的约束下,传统鲁棒滤波难以适应复杂时变的厚尾噪声的问题,本文以容积卡尔曼滤波器为框架,研究一种基于Pearson Type VII 分布的自适应滤波算法 (VBCKF Pearson).基于贝叶斯估计理论,选择Pearson Type VII 分布作为不确定厚尾噪声的共轭先验分布;建立基于目标状态、尺度矩阵、双自由度参数、辅助参数的联合后验概率密度函数,利用变分贝叶斯方法,求解联合后验分布中待估计参数的变分近似分布;在滤波更新中,利用容积采样规则,更新非线性函数的传递和新息协方差矩阵,实现对目标状态和不确定厚尾噪声的联合估计.
1 问题描述
考虑如下模型,
式中:k为采样时刻;x、f(·)和w分别为状态向量、状态转移函数和过程噪声,且w服从均值为0,协方差阵为Q的高斯分布,记作w~N(w;0,Q);z、h(·)分别为量测向量和观测函数;v为不确定厚尾噪声.
目前,针对厚尾噪声的鲁棒滤波算法假设量测噪声的尺度矩阵和自由度参数精确已知且不随时间变化,滤波结果依赖于给定的参数,且根据经验选取尺度矩阵和自由度参数存在一定的盲目性.对此,本文基于式(1)和(2)的模型,利用Pearson Type VII 分布和变分贝叶斯方法,将鲁棒滤波固定自由度参数的估计转化为Pearson Type VII 分布双自由度参数的估计,并对尺度矩阵和双自由度参数进行自适应联合估计.选择容积卡尔曼滤波器(CKF)为基础滤波器,具体算法见文献[16].
2 不确定厚尾噪声条件下的状态估计
2.1 共轭先验分布和时间更新
选择Pearson Type VII 分布作为未知量测噪声的先验分布.在此基础上,通过遗忘因子对噪声参数进行时间更新.
Pearson Type VII 分布可被描述为高斯分布与Gamma分布的卷积[17],其定义如下:
P(θ|ε,R,φ,σ)=
(3)
式中:θ为统计量;ε为均值;R为尺度矩阵;φ和σ为双自由度参数,且当φ=σ时,Pearson Type VII 分布即为Student’s t分布;N(·)为高斯分布;G(·)为Gamma分布;κ为辅助参数.P(θ|ε,R,φ,σ)表示θ服从于参数为ε、R、φ、σ的Pearson Type VII 分布.考虑量测噪声为不确定厚尾噪声,可选择Pearson Type VII 分布作为先验分布,表示为
p(vk)=P(vk|0,Rk,φk,σk)=
(4)
考虑Rk、κk、φk和σk的不确定性与时变性,分别选择inverse Wishart分布和Gamma分布作为先验分布,表示为
(5)
通过遗忘因子(ρ)对上述参数进行时间更新,
(6)
(7)
(8)
(9)
(10)
(11)
式中:nz为量测向量的维度;k|k-1为k-1到k时刻的预测;k-1|k-1为k-1时刻的估计.

(12)
(13)
(14)
(15)
(16)

2.2 基于变分贝叶斯的近似后验
在先验分布和时间更新的基础上,基于变分迭代思想对xk、Rk、κk、φk和σk的近似后验分布进行推导和求解.
在非线性系统中,系统状态和待估计参数的联合后验估计通常难以得到解析解.对此,可以利用变分贝叶斯方法得到近似后验分布.变分贝叶斯方法通过寻找真实分布(p(·))的近似分布(q(·)),使两者的相对熵(KL散度)取最小值[6],即
{q(·)}=arg min KLD(q(·)‖p(·))
(17)
KL散度可描述为
KLD(q(·)‖p(·))≡
(18)
在不确定厚尾噪声条件下,系统状态向量和尺度矩阵、双自由度参数以及辅助参数的联合后验分布及其近似分布可表示为
p(xk,Rk,φk,σk,κk|z1∶k)≈
q(xk)q(Rk)q(κk)q(φk)q(σk)
(19)
式中:1∶k表示时刻1到k;q(xk)、q(Rk)、q(κk)、q(φk)、q(σk) 分别为xk、Rk、κk、φk、σk的近似后验分布.则问题等价于
logq(ζ)=EΩ(-ζ)(logp(Ω,z1∶k))+cζ
(20)
Ω≡{xk,Rk,κk,φk,σk}
式中:Ω为待估计参数xk、Rk、κk、φk和σk的集合;ζ为Ω中的元素;E(·) 为期望操作符;Ω(-ζ)为ζ在Ω中的补集;cζ为与ζ有关的常数.则有
logq(xk)=cxk+
ERk,κk,φk,σk(logp(xk,Rk,κk,φk,σk,z1∶k))
(21)
logq(Rk)=cRk+
Exk,κk,φk,σk(logp(xk,Rk,κk,φk,σk,z1∶k))
(22)
logq(κk)=cκk+
Exk,Rk,φk,σk(logp(xk,Rk,κk,φk,σk,z1∶k))
(23)
logq(φk)=cφk+
Exk,κk,Rk,σk(logp(xk,Rk,κk,φk,σk,z1∶k))
(24)
logq(σk)=cσk+
Exk,κk,Rk,φk(logp(xk,Rk,κk,φk,σk,z1∶k))
(25)
联合后验概率密度函数为
p(Ω,z1∶k)=p(xk,Rk,κk,φk,σk,z1∶k)=
(26)
在每次的量测更新过程中进行变分迭代循环(j=0,1,2…,N′-1),N′为变分迭代次数.各参数估计如下.
当ζ=xk时,
logq(j+1)(ζ)=logq(j+1)(xk)=
0.5E(j)(κk)(zk-h(xk))T×
(27)

当ζ=Rk时,
logq(j+1)(ζ)=logq(j+1)(Rk)=
E[(zk-h(xk))(zk-h(xk))T]+cRk≈
(28)

(29)
E(j)(κk)E(j)[(zk-h(xk))(zk-h(xk))T]
(30)
当ζ=κk时,
logq(j+1)(ζ)=logq(j+1)(κk)=
E(j)[(zk-h(xk))(zk-h(xk))T]≈
E(i)[(zk-h(xk))(zk-h(xk))T]}κk
(31)


(32)
h(xk))(zk-h(xk))T]}+0.5E(j)(σk)
(33)
当ζ=φk时,
logq(j+1)(ζ)=logq(j+1)(φk)=
(34)

(35)
(36)
当ζ=σk时,
logq(j+1)(ζ)=logq(j+1)(σk)
(37)

(38)
0.5log(E(j)(φk))
(39)
根据各估计参数的后验近似分布,有
(40)
(41)
(42)
(43)
3 基于Pearson Type VII 分布的不确定厚尾噪声滤波

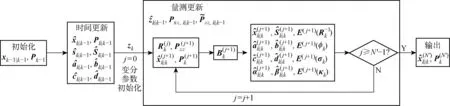
图1 算法流程图Fig.1 Flowchart of algorithm

步骤2根据式(6)~(11),通过遗忘因子对不确定厚尾噪声各参数进行时间更新.

(44)
(45)
Zi,k|k-1=h(Xi,k|k-1)
(46)
(49)
式中:Zi,k|k-1为将容积采样点Xi,k|k-1经量测方程传递后得到的量测预测值.
步骤4变分迭代.包括初始化变分参数和变分迭代循环(分为修正量测噪声协方差矩阵和量测误差协方差矩阵更新、状态更新、变分参数更新).其中,初始化变分参数包括
修正量测噪声协方差矩阵和量测误差协方差矩阵更新为
(50)
(51)
状态更新为
(52)
(53)
(54)


(55)
(56)
(57)
(58)
尺度矩阵的分布参数更新见式(29)~(30),双自由度参数的分布参数更新分别见式(35)~(36)和式(38)~(39),辅助参数分布参数更新见式(32)~(33),各待估计参数期望更新见式(40)~(43).
步骤5状态估计、误差协方差矩阵和分布参数更新.

与鲁棒容积卡尔曼(Robust CKF)算法相比,本文提出的VBCKF-Pearson算法可以实现尺度矩阵和双自由度参数的同时估计.现有Robust CKF算法假设尺度矩阵和自由度参数固定不变,根据经验选取参数存在一定的盲目性.本文算法选择Pearson Type VII 分布作为共轭先验,动态尺度矩阵描述了不确定量测噪声的矩阵参数,动态双自由度参数反映了不确定尺度矩阵和双自由度参数的自适应性.在相邻2个时刻的滤波过程中,Rk、φk、σk和κk的后验分布中的参数利用k时刻含厚尾噪声的量测进行更新;在一次滤波更新变分迭代中,Rk、κk、φk和σk相互耦合,其后验分布中的参数经式(29)~(44)不断被更新至近似分布与真实分布的KL散度最小,实现Rk、κk、φk和σk的同时估计.
4 仿真及分析
仿真系统为高维非线性目标跟踪系统,其目标在笛卡尔Oxy坐标系内运动.状态向量x=[sxvxsyvyω]T,sx和sy分别为x、y方向的位置,vx和vy分别为x、y方向的速度,ω为转弯速率,取 -π/60,T为采样周期,取1 s.目标运动方程[16]为
xk=Fxk-1+wk-1
(59)
式中:
wk-1~N(0,Qk-1)
Qk-1=
假设传感器位于坐标系原点,则量测方程可表示为
(60)
式中:
vk的协方差矩阵取Σk和100Σk的概率(p)分别为0.9和0.1.初始时刻的状态向量和状态误差协方差矩阵分别为
x0=[1 000 300 1 000 0 -π/60]
进行100次蒙特卡洛仿真,每次仿真时长(t)为100 s,变分迭代次数取N′=10.
仿真1滤波精度比较.比较Robust CKF和VBCKF Pearson算法的平均均方根误差(MRMSE),如表1所示,以及状态估计效果和均方根误差(RMSE),如图2所示.图中,VBCKF Pearson算法对各状态量的估计均方根误差均低于Robust CKF算法.表中,VBCKF Pearson算法对估计的sx、vx、sy、vy和ω的平均均方根误差比Robust CKF算法分别低22.2%、12.1%、17.6%、6.5%和2.4%.结果表明,在不确定厚尾噪声条件下,本文算法对目标的跟踪精度更高.

表1 平均均方根误差Tab.1 Mean of root mean square error

图2 Robust CKF和VBCKF Pearson算法的均方根误差Fig.2 RMSE of Robust CKF and VBCKF Pearson algorithms
仿真2参数分析.为了进一步研究VBCKF Pearson算法的性能,对比了3种算法对目标状态的估计效果和均方根误差,如图3所示,以及各算法的平均均方根误差,已在表1中展示.其中,VBCKF Pearson-R算法固定参数φ、σ并同时估计尺度矩阵和状态量,VBCKF Pearson-r算法固定尺度矩阵并同时估计状态量和φ、σ,VBCKF Pearson算法同时估计状态量、尺度矩阵和参数φ、σ.

图3 不同VBCKF Pearson算法的均方根误差Fig.3 RMSE of different VBCKF Pearson algorithms
图3中,VBCKF Pearson算法对sx估计的均方根误差最小,VBCKF Pearson-r算法次之,VBCKF Pearson-R算法最大.VBCKF Pearson算法对vx的估计误差均低于20 m/s.且其目标状态量估计的均方根误差均最低.表1中,VBCKF Pearson算法对sx、vx、sy、vy和ω的平均均方根误差比VBCKF Pearson-R算法分别低33.6%、21.4%、33.9%、19.8%和7.1%,比VBCKF Pearson-r算法分别低23.6%、17.7%、24.6%、15.1%和6.1%.这是由于量测噪声的不确定信息不仅包含在尺度矩阵中,还包含在参数φ、σ中.仅估计尺度矩阵而固定φ和σ,或仅估计φ和σ而固定尺度矩阵都会限制信息的自适应更新.所以,同时估计各参数更利于充分利用量测信息对目标状态进行估计.
仿真3计算复杂度分析.采用浮点运算数 (flops)进行计算复杂度分析[18].Robust CKF和VBCKF Pearson算法的浮点运算数分别为

式中:flops3和flops4分别为对数运算和digamma函数的浮点运算数.

5 结语
提出一种不确定厚尾噪声条件下的自适应滤波算法.针对传统鲁棒容积卡尔曼滤波器无法估计时变不准确的尺度矩阵和自由度参数的问题,选择Pearson Type VII 分布对不确定厚尾噪声进行建模,并分别选择inverse Wishart和Gamma分布作为Pearson Type VII 分布参数的先验分布.在此基础上,利用变分贝叶斯方法,实现状态向量、双自由度参数、辅助参数和尺度矩阵的联合估计.仿真结果表明,在不确定厚尾噪声条件下,本文算法的滤波精度高于传统鲁棒容积卡尔曼滤波算法.
