适应坡道行驶的多性能综合最优换挡规律*

卢 汉，阴晓峰，陈柯序，武小花，梁益铭，刘 阳

（1.西华大学汽车工程研究所，成都 610039； 2.攀枝花学院汽车与交通工程学院，攀枝花 617000）

前言

换挡规律是指汽车各挡间自动换挡时刻随控制参数变化的规律［1］。传统换挡规律通常是根据平直良好路面行驶工况制定的，由于没有考虑坡道对换挡性能的影响，当汽车在坡道上行驶时如果仍采用这种换挡规律，将明显降低汽车性能［2］。为提高自动变速汽车对坡道行驶的适应能力，国内外学者对坡道换挡规律进行了广泛的研究。Hebbale等［3］和Lei等［4］根据纵向动力学由坡道阻力获得一个在0到1之间的修正因子，然后在最大载荷动力性换挡规律和无载荷换挡规律之间进行插值，获得新换挡规律以适应不同坡度。孔慧芳等［5］和赵志国等［6］应用模糊逻辑修正平路上的换挡规律，取得了较好的效果。马文杰等［7］和詹军等［8］通过延迟平路换挡规律的换挡时刻，修正坡道行驶时的换挡车速。史俊武等［9］在辨识广义坡道的基础上，以动力性最优为目标，求解得到坡道换挡规律并通过实车道路试验进行了验证。刘振军等［10］提出了基于Takagi-Sugeno模型的模糊神经网络，将其应用于汽车自动变速器最佳挡位决策系统，仿真结果表明该系统提高了车辆适应坡道行驶的能力。Meng等［11］先计算出以加速度、油门开度、发动机转速为参数的换挡规律，再将其转变为以坡道、油门开度、发动机转速为参数的换挡规律，仿真结果表明此方法能使车辆适应坡道变化。

上述方法能有效减少频繁换挡，但没有在换挡规律的修正中兼顾动力性和燃油经济性需求。本文中从多种性能综合最优的角度出发，在体现个性化驾驶风格、兼顾整车动力性和燃油经济性的同时，提出了适应坡道行驶的多性能综合最优换挡规律优化方法。

1 坡道对换挡的影响

汽车使用未考虑坡道因素的换挡规律在坡道上行驶时，可能会产生循环换挡，如图1所示。车辆在A点以2挡行驶在坡道上，由于此时坡道行驶阻力小于2挡驱动力，汽车加速行驶，车速在B点达到换挡点，换入3挡，即图中C点，但由于坡道行驶阻力大于3挡驱动力，车速下降，至D点达到降挡点，降至2挡，即A点，而2挡的驱动力大于坡道行驶阻力，车速又一次升到B点，挡位将在2挡和3挡之间不断循环。因此在制定坡道换挡规律时，须考虑道路坡度的影响。

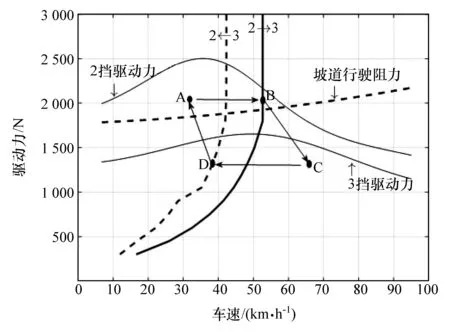
图1 坡道行驶换挡循环示意图

汽车在坡道上行驶时，换挡后须具备足够的驱动力，即只有换挡后的驱动力大于或等于行驶阻力，才能确保通过坡道不产生循环换挡。以试验车在85%油门开度下坡道行驶为例，绘制该车在该油门开度下驱动力与不同坡度下的行驶阻力，如图2所示。由图可见，在该油门开度下，车速小于66.3 km／h时，1和2挡的驱动力大于12°坡道行驶阻力，而3、4和5挡驱动力曲线在所有车速下均在12°坡道行驶阻力曲线之下。因此，该车在该油门开度下在12°坡道上行驶时，车速小于66.3 km／h时应选择1挡或2挡，以确保通过坡道不会产生换挡循环。通过分析不同节气门开度下各挡驱动力与不同坡度行驶阻力之间的关系，可确定不同油门开度和不同坡度组合下合理的挡位范围。

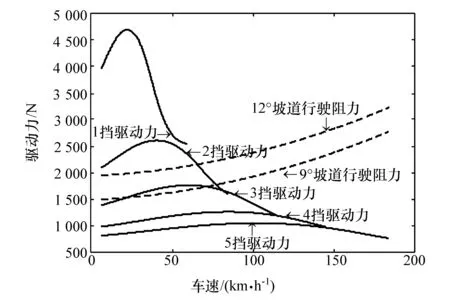
图2 驱动力与行驶阻力平衡图

2 适应坡道行驶的多性能综合换挡规律优化方法

为适应不同的驾驶风格和提升车辆的整体性能，应在制定换挡规律时综合考虑驾驶员的性能倾向，兼顾车辆的动力性和燃油经济性指标［12］，属多目标优化问题。本文中采用理想点与平方和线性加权法［13］将驾驶员的性能倾向与动力性和经济性分目标函数相结合，构造综合性能评价函数，然后采用遗传算法寻找在不同驾驶员性能倾向、不同坡度和不同油门开度下综合性能最优的换挡车速。

2.1 优化问题描述

本文中采用油门开度和车速为换挡控制参数，当油门开度一定时，换挡点的选择只与车速有关，故选择车速作为决策变量，分别去求解不同油门开度下的换挡点。

2.1.1 目标函数

（1）动力性分目标函数

汽车动力性最优的理想情况是使自动变速器在相邻两挡加速度曲线交点所对应的车速换挡。故动力性分目标函数可用同一油门开度下相邻两挡加速度之差的绝对值表示。

式中：i为挡位；uai为i挡车速，km／h；d uai／d t为i挡加速度，m／s2；fd（ua）为动力性分目标函数，若函数值为0，即在相邻两挡加速度相等时换挡，汽车动力性最好。

（2）经济性分目标函数

类似地，若在相邻挡位燃油消耗率曲线交点所对应的车速换挡，可使汽车在燃油消耗率最小的挡位行驶，燃油经济性最佳。故经济性分目标函数可使用同一油门开度下相邻两挡燃油消耗率之差的绝对值表示。

式中：ffc（ua）为经济性分目标函数；bei为i挡对应的发动机燃油消耗率。

（3）综合性能评价函数

为提高换挡规律对驾驶员换挡性能期望的灵敏性，采用理想点与平方和线性加权法构造综合性能评价函数f（ua）。

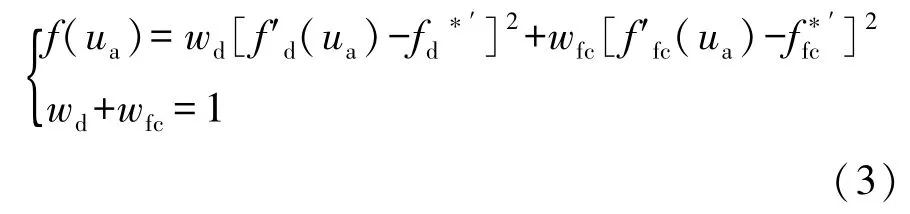
式中：wd、wfc分别为动力性指标、经济性指标的权系数，表示驾驶员的换挡性能倾向，用以体现个性化驾驶风格；f′d（ua）、f′fc（ua）分别为归一化后的动力性和经济性分目标函数；fd*′为归一化后的最佳动力性指标。

不同wd和wfc的组合，可体现驾驶者不同的操纵意图，若wd的值相对较大，则表示驾驶者希望以动力性为主，同时兼顾经济性；若驾驶者更倾向于汽车具有较好的燃油经济性，则wfc的取值应相对较大。

式（3）中涉及的归一化方法，可表示为

式中：x′为归一化后的值；x为实际值；xmax和xmin分别为样本数据的最大值和最小值。

2.1.2 约束条件

（1）汽车坡道行驶约束条件

汽车在坡道上行驶时，换挡后的驱动力应大于或等于行驶阻力，即应满足

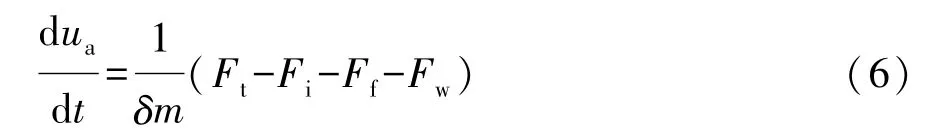
式中：δ为回转质量转换系数；m为整车质量，kg；Ft为汽车驱动力，N；Fi为坡道阻力，N；Ff为滚动阻力，N；Fw为空气阻力，N。

（2）发动机转速约束条件

车辆行驶中发动机转速应在当前油门对应最低稳定转速和最高转速之间，约束条件为

式中：nemin、nemax分别为发动机最低稳定转速和最高转速，r／min；i0为主减速器传动比；ig为变速器的传动比；r为车轮半径，m。

2.1.3 优化问题模型

结合式（3）、式（5）、式（7）和式（8），适应坡道行驶的多性能综合最优换挡规律优化问题的数学模型可描述为

2.2 优化方法

优化问题的常见求解方法主要有梯度算法和非梯度算法两类。梯度算法对目标函数的要求较高，得到的结果通常为局部最优；非梯度算法不需要梯度信息，能够全局搜索避免所得结果陷入局部最优。遗传算法作为非梯度算法的一种，全局搜索能力强，在工程领域得到广泛应用［14］，与模拟退火算法、蚁群算法等非梯度算法相比，其获得全局最优解的概率更大。因此，本文中采用遗传算法对适应坡度变化的多性能综合最优换挡规律进行优化。

遗传算法是一种模仿自然界中生物遗传进化机理的随机搜索算法。基本过程是先在解的区间范围内生成初始种群，该种群是由一定数量、通过二进制编码的个体组成，其中每个个体称为染色体，不同个体通过染色体的选择、交叉和变异生成新的个体，依照适者生存的规则，通过若干代的进化最终得到条件最优的个体［13］。

对适应坡度变化的多性能综合最优换挡规律进行求解。首先，根据不同坡度下坡道行驶阻力与驱动力的平衡关系确定允许使用的挡位；其次，确定该坡度下各个油门开度下允许使用挡位的车速范围，进而确定各坡度和油门开度下相邻两挡换挡车速的搜索范围；然后，在给定坡度和各分目标（对应各分性能指标）权值的条件下，在允许使用的挡位和车速范围内，遍历不同的油门开度；最后，采用遗传算法求解出使该坡度和权值下综合性能最优的换挡点车速，得到适应该坡道行驶、并体现由给定权值组合所反映的驾驶性能期望的多性能综合最优换挡规律。给定坡度和分性能指标权值下换挡规律优化流程如图3所示。其中，n为当前最大挡位数；i为当前挡位；θ为坡度角；k为油门开度α从0到100%的等分数；j为当前油门开度值在升序排列后的油门开度值中的序号；uaup为升挡车速；uadown为降挡车速。改变分目标权值组合，采用前述方法，可优化得到该坡度下不同驾驶风格对应的换挡规律。改变坡度，重复前述优化过程，即可得到在不同坡度下不同驾驶风格对应的换挡规律。

图3 主流程图

在给定油门开度下，采用遗传算法求解设定坡度和权值下的综合性能最优的换挡点车速的具体过程为：将当前条件下允许的换挡车速，按其范围上限和下限分别对应于10位二进制数的最大值和最小值，根据其实际大小编码长度为10的二进制串；并于其中随机选取20个个体生成初始种群，以综合评价函数为基础构造适应度函数；在采用轮盘赌选择算法构造新种群的基础上通过交叉和变异产生新的个体，重复选择、交叉和变异操作，直到适应度值的变化满足终止条件或进化次数达到设定值；再通过解码可得当前条件下综合性能最优的换挡点车速。

3 换挡规律优化实例与仿真验证

3.1 优化实例

应用所提出的坡道行驶多性能综合最优换挡规律优化方法，针对某一5挡机械式自动变速器（automated manual transmission，AMT）轿车（其整车及传动系统主要参数如表1所示），制定了各种驾驶员性能倾向（由不同权值组合体现）下适应不同坡道行驶的多性能综合最优换挡规律。

表1 试验轿车参数

限于篇幅，仅列出部分坡道换挡规律优化结果，分别如图4和图5所示。图4（a）～图4（c）分别为4°、8°和12°坡道的动力性占优（wd＝0.8，wfc＝0.2）换挡规律曲线。图5（a）～图5（c）分别为4°、8°和12°坡道的经济性占优（wd＝0.2，wfc＝0.8）换挡规律曲线。

由图4和图5可知，随着坡度的增加，允许行驶的最高挡位逐渐降低，该车在4°、8°和12°坡道上行驶允许的最高挡位分别为4挡、3挡和2挡。与动力性占优换挡相比，经济性占优换挡规律在同一油门开度下、同一挡位升至相邻挡位的车速更低。

图4 动力性占优坡道换挡规律

3.2 仿真分析

为验证坡道行驶多性能综合最优换挡规律优化方法的有效性，建立了换挡规律仿真评价系统，该系统由发动机模型、AMT仿真模块、整车纵向动力学模块、换挡逻辑仿真模块以及修改后的可变坡度高速公路循环工况（HWFET-MTN）模块等组成［15］。在建立的换挡规律仿真评价系统中使用优化后考虑坡道和未考虑坡道的多性能综合最优换挡规律（本文中，前者简称为坡道换挡规律，后者简称为常规换挡规律），完成了定油门和变油门坡道行驶仿真以及定坡度动力性仿真。在定油门坡道行驶仿真中完成了定油门定坡道和定油门变坡道两种工况仿真；在变油门坡道行驶仿真中完成了变油门定坡道循环工况和变油门变坡道循环工况仿真。

（1）定油门坡道行驶仿真

油门开度为20%，并使用经济性占优换挡规律，分别完成了定坡度和变坡度仿真。定坡度仿真的坡度角取8°；变坡度仿真中坡度角按4°-8°-12°顺序变化。

图5 经济性占优坡道换挡规律

图6为定油门8°坡道行驶仿真结果，汽车在60 s时驶入8°坡道，图6（a）为挡位和坡道阻力变化情况，图6（b）为车速变化曲线。由图可知，使用坡道换挡规律的汽车始终使用3挡行驶，车速变化平稳；而使用常规换挡规律的汽车在87 s时换入4挡，汽车减速行驶，最后又换回3挡，之后车速再上升，存在循环换挡现象。

图7为定油门4°-8°-12°坡道行驶仿真结果，汽车60 s时驶入4°坡道，120 s时驶入8°坡道，200 s时驶入12°坡道。图7（a）为挡位和坡道阻力变化情况，图7（b）为车速变化曲线。由图可知，使用常规换挡规律的汽车在每段坡道上均存在循环换挡现象，车速波动较大；而使用坡道换挡规律的汽车则能在每段坡道上选择合适的挡位行驶，不会产生循环换挡，车速波动较小。

（2）变油门坡道行驶仿真

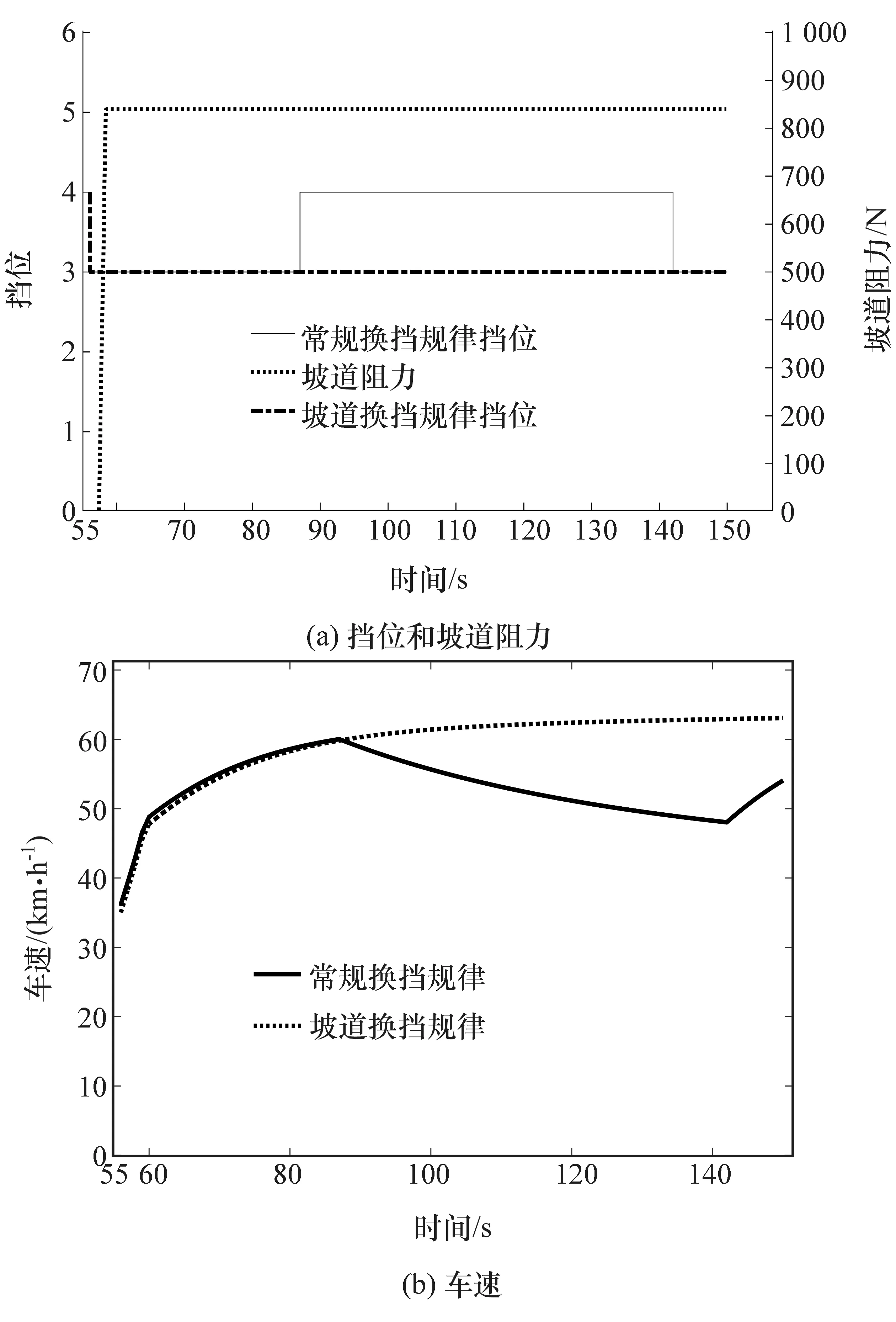
图6 定油门8°坡道行驶仿真结果

为验证坡道换挡规律在坡道循环工况下的性能，对HWFET-MTN工况进行了修改，使其包含仿真坡道信息，并使其车速更符合城市道路行驶状况，修改后的HWFET-MTN工况如图8所示。

控制系统通过调节油门开度实现对循环工况车速的跟踪，仿真道路条件为汽车先在平路行驶100 s，之后驶入坡道，在137 s时坡道结束，坡长为511.25 m。分别完成了定坡度和变坡度仿真，其中，定坡度仿真的坡度角为8°；变坡度仿真中坡度角按4°-8°-12°顺序变化。由于在坡道之外均为平路（在此情况下坡道换挡规律和常规换挡规律相同），为更清晰地比较常规换挡规律和坡道换挡规律在坡道上的换挡情况，仅取含坡道在内的部分结果绘制仿真曲线。

图9为变油门8°坡道行驶仿真结果，图9（a）为车速变化情况，图9（b）为坡道阻力变化情况，图9（c）为挡位变化曲线。由图可知，汽车从100 s开始爬坡，为跟踪目标车速，控制系统增大油门开度，汽车因油门开度变化产生降挡行为（5挡降4挡再降至3挡）。在随后的上坡过程中，采用常规换挡规律的汽车在3挡和4挡之间形成换挡循环，直至通过坡道；而采用坡道换挡规律的汽车则在随后的上坡过程一直保持在3挡，在整个道坡行驶过程只有2次换挡。

图7 定油门4°-8°-12°坡道行驶仿真结果

图8 修改后的HWFET-MTN循环工况

图10为变油门4°-8°-12°坡道行驶仿真结果，汽车在100 s时开始驶入4°坡道，111 s时驶入8°坡道，126.5 s时驶入12°坡道。图10（a）为车速变化情况，图10（b）为坡道阻力变化情况，图10（c）为挡位变化曲线。由图可知，使用常规换挡规律的汽车在每段坡道上均存在循环换挡现象，而使用坡道换挡规律的汽车则能在每段坡道上均选择合适的挡位行驶，不会产生循环换挡。

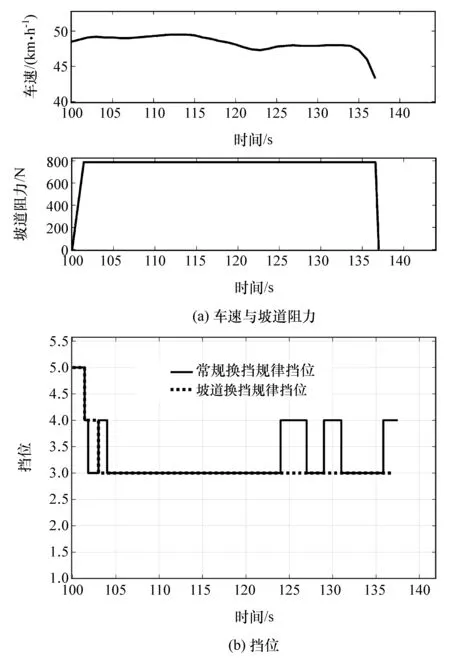
图9 变油门8°坡道行驶仿真结果

表2为使用两种换挡规律的汽车在循环工况下的油耗与坡道换挡次数对比情况。由表可知，坡道换挡规律以油耗略增（增幅分别为0.81%和0.79%）为代价，有效地降低了非预期坡道换挡次数，消除了坡道换挡循环。

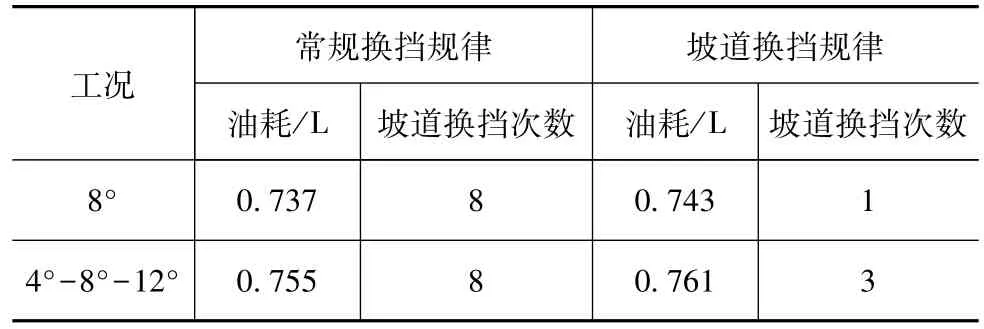
表2 循环工况油耗与坡道换挡次数

（3）定坡度动力性仿真

为了验证多性能综合最优坡道换挡规律的动力性，参考GB／T12543—2009《汽车加速性能试验方法》，将该标准试验条件中的平直路面改为坡道路面，使用不同的动力性权值使车辆由静止状态加速通过400 m坡道的行驶时间作为动力性评价指标。限于篇幅，仅以8°坡道为例，不同动力权值下多性能综合最优坡道换挡规律动力性仿真结果如表3所示。

图10 变油门4°-8°-12°坡道行驶仿真结果

表3 不同动力性权值8°坡道行驶时间

由表3可知，汽车通过400 m长的8°坡道行驶时间，随着动力性权值的增大而减少，表明所制定的多性能综合最优坡道换挡规律能够反映驾驶者的性能需求意图。

4 结论

在分析坡道行驶汽车换挡循环产生原因的基础上，针对考虑驾驶意图的多性能综合最优换挡问题，使用理想点与平方和线性加权法建立了兼顾动力性和经济性、同时又体现驾驶员换挡性能倾向的综合性能评价函数，将坡道因素引入约束条件之中，设计了基于遗传算法的坡道行驶多性能综合最优换挡规律优化方法。

在定油门定坡道、定油门变坡道、变油门定坡道循环工况、变油门变坡道循环工况下对考虑坡道和未考虑坡道的多性能综合最优换挡规律进行了仿真。仿真结果表明：适应坡道行驶的多性能综合最优换挡规律可消除有级自动变速器在坡道上的非预期换挡问题，减少换挡次数，提高乘坐舒适性。在修改后的HWFET-MTN循环工况下，采用适应道路行驶的多性能综合最优换挡规律的汽车，其燃油经济性略低于常规换挡规律。定坡度动力性仿真结果亦表明制定的多性能综合最优坡道换挡规律能够反映驾驶者的性能需求意图。