基于地图信息和循环SVR模型的纯电动汽车续驶里程预测*

田慧欣，李晓宇，刘 芳

（1.天津工业大学电气工程与自动化学院，天津 300387； 2.天津工业大学，电工电能新技术天津重点实验室，天津 300387；3.天津工业大学计算科学与技术学院，天津 300387）

前言

由于纯电动汽车完全不涉及燃油，对环境友好，其发展前景备受关注。我国的新能源汽车计划以发展纯电动汽车为主，因此纯电动汽车有着极大的市场和非常好的发展前景，由于目前我国的电动车充电设施还处于建设阶段，较少的充电设施要求驾驶员出行前要对路线有所规划，但由于纯电动汽车的能耗受行驶道路与环境的影响较大，厂家提供的续驶里程往往与实际可行驶里程不符，不能对驾驶员起到很好的行车指导作用，使驾驶员容易产生“里程焦虑”，降低了人们对电动汽车的使用信心［1］。

为更精准地预测纯电动汽车的剩余续驶里程，推动电动汽车行业的发展，越来越多的学者开始关注续驶里程的预测，并提出了许多行之有效的办法。文献［2］中考虑到等速法存在的精度和适用性问题，提出了基于工况法的试验方法，研究了不同工况对续驶里程预测精度的影响。文献［3］和文献［4］中分析了影响电动汽车续驶里程的因素，为以后的研究提供基础。文献［5］和文献［6］中根据车辆在前一段时间的平均能耗和电池剩余能量来估算车辆未来行驶能耗和剩余续驶里程。这些方法预测结果较保守，且在工况急剧变化的情况下预测结果不稳定。为进一步提高剩余续驶里程的预测精度，本文中提出了一种基于地图信息和循环支持向量回归（support vector regression，SVR）模型的纯电动汽车剩余续驶里程预测方法。该方法利用百度地图的路径规划功能获取每段行程的道路类型和路况信息推测未来的行驶工况，并构建循环SVR来预测续驶里程。该方法包括以下3个步骤。

（1）工况数据采集与分析。工况数据的采集与分析是实现该方法的基础。利用高级车辆仿真器（advanced vehIcle simulator，ADVISOR）采集电动汽车的运行数据，并将数据划分成多个工况片段。提取这些工况片段的特征参数，并依据所提取特征参数对工况片段进行聚类，得到4种典型工况。

（2）地图信息融合。地图信息融合指利用电子地图的路径规划功能，获取未来行驶过程中的道路类型和路况指数等信息，并将这些信息与4种典型工况对应起来，实现对未来工况的预测。

（3）循环SVR模型构建。循环SVR的构建分两步进行：一是构建基本SVR模型，实现在不同工况和SOC值的条件下对ΔSOC的估算；二是构建循环SVR模型，利用地图信息预测出未来工况，在SOC＞0时循环计算ΔSOC和剩余的SOC，最终计算出剩余续驶里程。

1 工况数据采集和分析

1.1 行驶工况数据收集

数据收集是工况片段划分和特征分析的基础。利用ADVISOR软件可模拟各种常用测试工况下电动汽车的行驶过程，获得车辆在不同工况、不同条件下的运行数据。

选择ADVISOR软件中EV1型电动汽车进行数据采集，汽车参数如表1所示［7］。设置电池包中单体电池个数为100，其他参数为默认值，在此基础上进行数据采集以获得原始数据集，并多次变化运行工况和初始条件以保证数据的多样性。

1.2 工况片段划分和特征提取

一般车辆的行驶过程是一个连续的过程，在行驶过程中行驶工况会不断发生变化。为更有效地识别工况类型和分析行驶工况与剩余续驶里程之间的关系，须对1.1节中的原始数据进行片段划分。

划分行驶工况片段的常用方法有短行程划分法和定步长划分法［8］两类。其中短行程划分法是指将两个相邻的停车点之间的行驶里程定义为一个数据单元。而定步长划分法则是按照一定时间长度将行驶工况划分若干段，将每一段车辆行驶里程定义为一个数据单元。本文中使用定步长划分法，并将所采集的数据按步长120 s划分为多个片段。图1为片段划分示例。

对原始数据进行片段划分后共得到11 543个工况片段，这些片段中的行驶工况以速度曲线来表征，从速度曲线中可以提取多种特征参数。利用这些特征参数进行工况分类与识别，目前常用的工况特征参数约有60种。但是公认的最能表征工况信息，且与电量消耗关系较大的有4种：平均速度、怠速时间占比、最大速度和速度标准差［9］。这4种参数的符号、名称和单位如表2所示。

对工况片段的上述特征参数进行提取并保存，为后续的工况片段聚类和SVR模型建立提供依据。

图1 片段划分示例

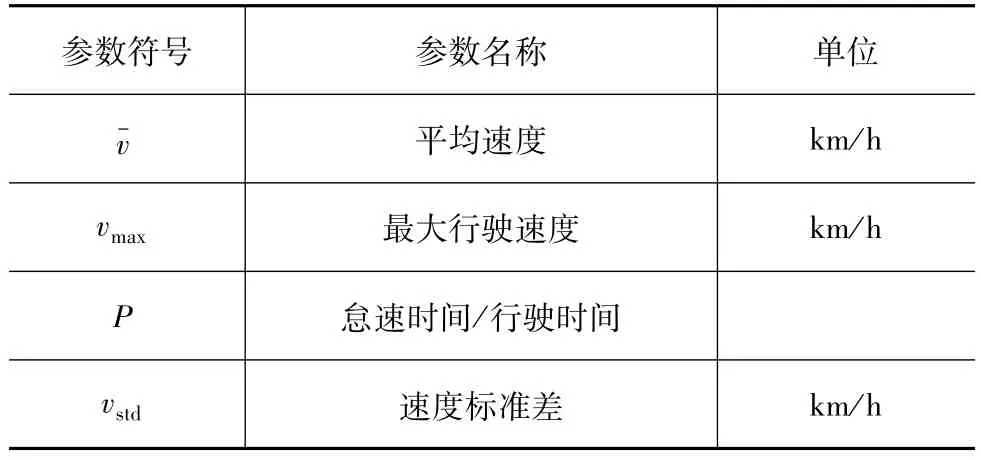
表2 参数的属性

1.3 工况片段聚类

由于地图信息有限，且提取的工况片段之间部分片段存在一定相似性，为便于利用地图信息推测未来的行驶工况，须对工况片段进行聚类分析。

聚类分析是数据分析的一种常用方法，该方法能在没有先验信息的指导下，对样本对象进行分类。K-均值聚类（K-means）算法由于其易于实现和出色的运行速度，一直是最常用的聚类算法之一。它属于无监督学习算法，其思想是基于质心技术，先将样本按类聚集，计算出初始的聚类中心，再不断迭代更新聚类中心，直到中心点的位置不再改变为止。

由于在利用ADVISOR获取实验数据的过程中，每次都设置电动汽车在某一工况下反复运行直至电量耗尽，且在每种工况下都变换实验初始条件测出了多组数据，所以在提取17 324个工况片段中有许多片段的工况参数相同，去除这部分重复数据，共计有工况参数不同的工况片段1 072个。使用K-means算法对工况片段进行聚类，设置聚类中心个数为4，得到聚类中心结果如表3所示。利用Matlab中的mdscale函数将片段特征的四维数据转化为二维坐标之后的聚类结果如图2所示。

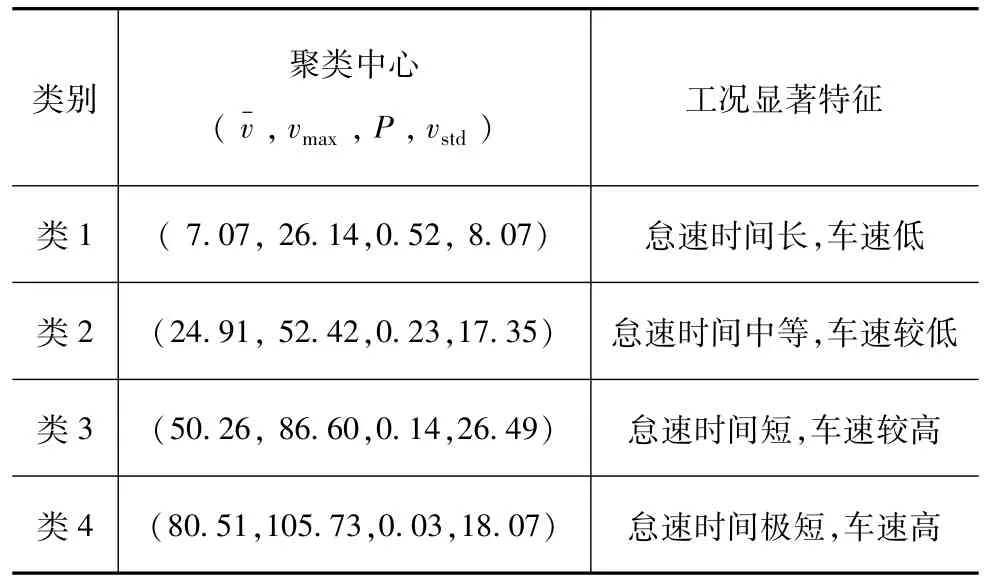
表3 4类工况的聚类中心

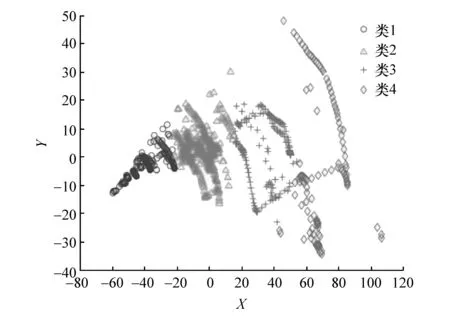
图2 坐标转化后的聚类结果

这4种聚类类别可与生活中的4种典型路况相对应：类1为城市拥堵工况，怠速时间长，车速低；类2为城市低速工况，怠速时间中等，车速较低；类3为郊区／城市畅通工况，怠速时间短，车速较高；类4为高速工况，怠速时间极短，车速高。根据工况类别的这些特征，再与地图信息相融合，即可对车辆行驶中未来的工况做更精准的推测。

2 地图信息融合

现有的续驶里程估算中，常用当前工况去预测未来工况，该方法存在较大误差。随着车载导航系统的发展，利用地图信息预测未来的工况成为可能。以百度地图为例，使用百度地图进行路径规划，其返回的数据中包含道路类型和路况指数等信息，利用这些信息做指导，可实现未来工况的精确预测。

百度地图中的道路类型有10种（以0～9的编号表示），各编号的含义如表4所示。其中7、8、9这3种编号代表的道路类型为非机动车道，在对电动汽车驾驶路径规划中一般不会出现。路况指数有5种（以0～4的编号表示），各编号的含义如表5所示。

表4 道路类型

表5 路况指数

在道路类型和路况信息已知的情况下，可对行驶工况进行相应的估计。在估计前，对差异不大的道路类型进行归纳，将10种道路类型简化为4个类别：高速路和城市高速路记为高速；国道和省道记为一级道路；县道和乡镇道路记为二级道路；其余道路均记为其它。之后，根据经验，建立道路类型、路况信息和4种典型工况之间的对应关系如表6所示。

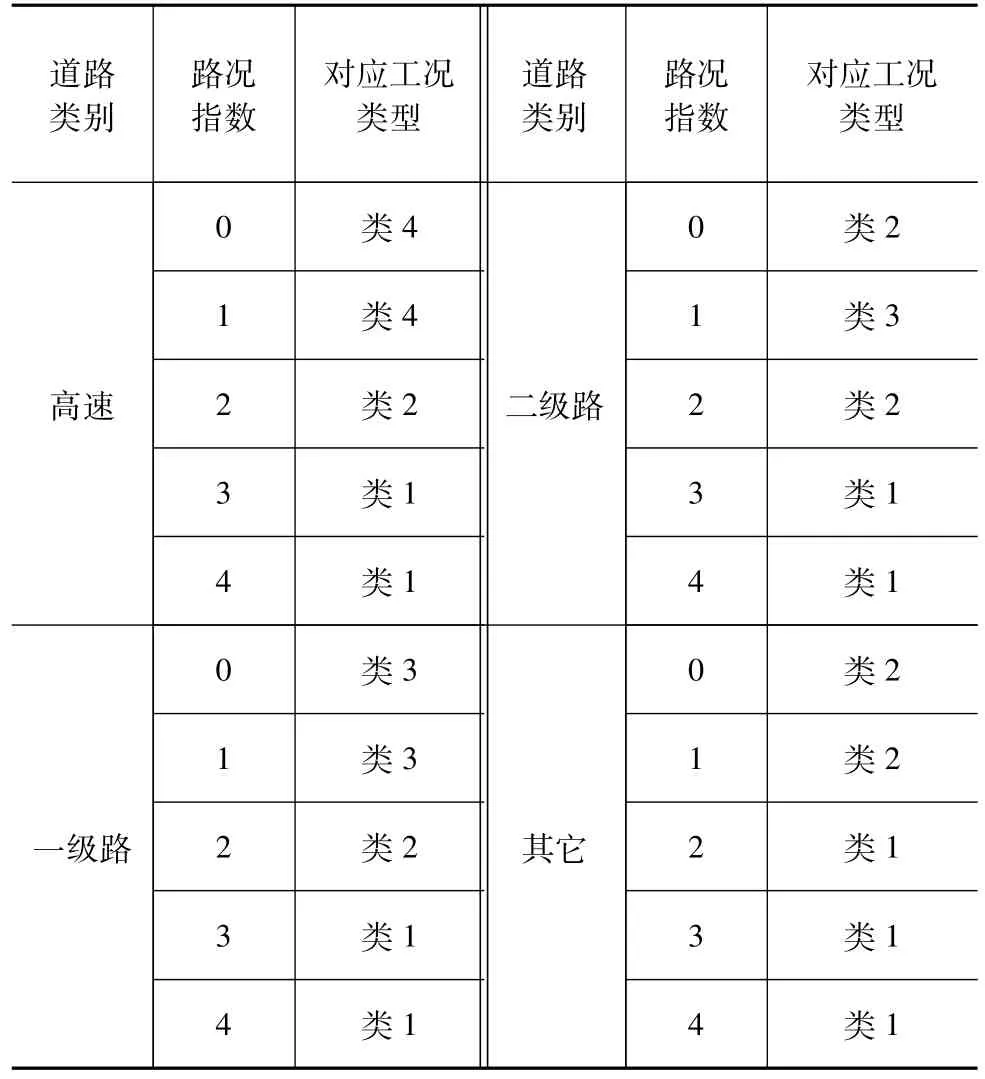
表6 道路类型、路况信息和工况之间的对应关系

3 循环SVR模型构建

3.1 SVR原理

支持向量机（support vector machine，SVM）是由Cortes和Vapnik等［10］于1995年提出的，其理论根据是统计学习理论中的结构风险最小化原则。该方法能处理分类问题与回归问题，在处理小样本、非线性和高维模型时比其它算法有明显的优势。支持向量回归（SVM）是在解决回归问题时的扩展形式。SVR能以任意精度逼近任何非线性连续函数，广泛应用于非线性系统参数预测和软测量等领域。

支持向量回归原理是：对于给定训练数据集S＝｛（x1，y1），（x2，y2），…，（xl，yl）｝，其中，xi∈Rn为多维输入向量，yi∈Rn（R为实数集）为一维输出，i＝1，2，…，l，Rn为n维向量空间，SVR的目标是寻找回归函数f（x），使f（x）与输出y的偏差最小。回归函数f（x）为

式中：w为权重矢量；b为偏置参数。

通过数据训练使式（1）的结构化风险最小，即y与f（x）最为接近。为此引入松弛因子和不敏感损失函数Lε，并将上述问题转化为一个优化问题：

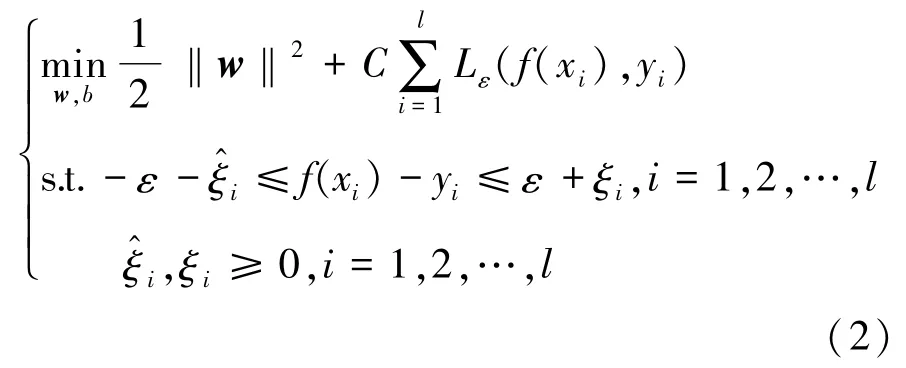
式中：C（C＞0且为常数）称为惩罚因子，用于平衡算法复杂度与样本回归误差之间的权重；ε为不敏感系数，表示模型对样本误差的允许程度，一般ε设置为一个非常小的正数。不敏感损失函数Lε的定义如式（3）所示。

之后利用拉格朗日函数和对偶方法求解式（2），则可求得SVR的解为

式中：αi≥0，为引入的拉格朗日乘子；α*＝为最优解；K（xi，xj）为核函数，其功能是通过某种非线性映射将低维数据映射到高维空间，使非线性问题可用线性方法来处理，以降低算法的复杂度，减少计算量。常用的核函数有多种，如高斯核函数和多项式核函数等。本文中选用高斯核函数。在训练样本较少、数据间存在非线性关系时，该函数的效果明显优于其它函数。高斯核函数定义为

式中g为核参数。

3.2 基本SVR模型的构建

在现有研究中，一般认为在车辆性能一定的情况下，车辆的行驶里程与行驶工况和环境温度密切相关。

图3示出1.1节中所设置的EV1型电动汽车在几种不同工况下的续驶里程。其中ECE工况是市区行驶工况；EUDC工况是郊区行驶工况；NEDC则是由4个ECE工况和1个EUDC工况组成，可视为混合工况；WVUCITY工况是城市拥堵工况；CON60为车速60 mile／h的匀速行驶工况（1 mile约为1.609 km）；CON45为车速45 mile／h的匀速行驶工况。

图3 不同工况下的电动汽车续驶里程

从图3可以看出不同工况汽车的续驶里程明显不同。ECE、EUDC和NEDC 3种工况中，ECE工况的续驶里程最短，而EUDC下的续驶里程最长，NEDC的续驶里程介于两者之间。这是由于市区工况（ECE）中的驻车次数较多，车速不稳定，使续驶里程较短；而郊区工况（EUDC）中，只有几次驻车，车速也相对平稳，使续驶里程较长。在城市拥堵工况（WVUCITY）下续驶里程更是大幅缩短，说明车速越平稳，驻车次数越少，续驶里程则越长。两种匀速工况中，CON45的续驶里程明显大于CON60，说明在匀速行驶时，车速越高，能耗越大，续驶里程越短。因此，如果车辆在平均车速较小且车速比较平稳的工况下运行，车辆的续驶里程就会相对增加。

温度也会明显影响汽车的续驶里程。其影响主要体现在对动力电池性能的影响。对于电池来说，虽然温度并不会改变其容量，但如果电池在低温环境下放电，电池放电平台（稳定放电电压）也会跟着温度的下降而降低。因此，与常温相比，低温环境下电池的SOC每下降1%所释放出的能量较少，因而低温环境下汽车的续驶里程变短。

此外，根据电池放电特性曲线（见图4），随着SOC的降低电池放电电压降低，释放同样的电量时所输出的能量减少，当SOC低于20%时单位里程SOC下降值会明显增大。

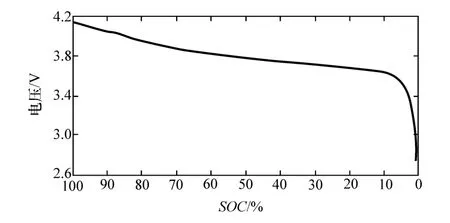
图4 电池放电特性曲线

综上所述，单位里程SOC变化量ΔSOC取决于行驶路况、当前电池组SOC和温度等因素，且这些因素之间存在复杂的非线性关系，难以用具体的函数去描述。故本文选择利用SVR模型对单位里程SOC变化量（ΔSOC）进行估算，模型的输入为工况种类、温度和当前时刻SOC（SOC0）。

选取10 000个片段进行建模，3 000个片段进行测试，图5和图6为其中1 000个测试样本的估算结果和估算误差。测试的最大绝对误差为0.046%，均方根为0.0147%，平均绝对误差为0.0128%。按照此模型的精度，如果在行驶中能准确预知未来行驶过程中的工况信息，则对于一辆标定续驶里程（满电情况下的续驶里程）为400 km的电动汽车，其续驶里程估算误差不会超过20 km。由于同一工况类别不同片段的工况仍存在一定差异，故模型精度的提高受到一定限制，可认为此模型的精度已可满足在续驶里程预测中对单位里程SOC下降值进行估算的要求。

图5 模型估算效果

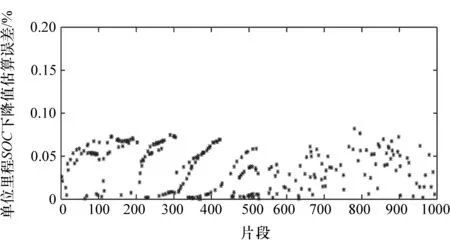
图6 模型误差

3.3 循环SVR模型

模型的流程如图7所示。以3.2节中的基本SVR模型为核心，并利用地图信息来推测未来的行驶工况，估算未来1 km的SOC下降值ΔSOC。在此基础上，用SOC减去ΔSOC得到剩余的SOC，再次估算下个1 km的ΔSOC。重复这个循环，直至SOC＝0或者小于某个设定值时循环结束。模型的循环次数便等于电动汽车的剩余续驶里程R的数值。

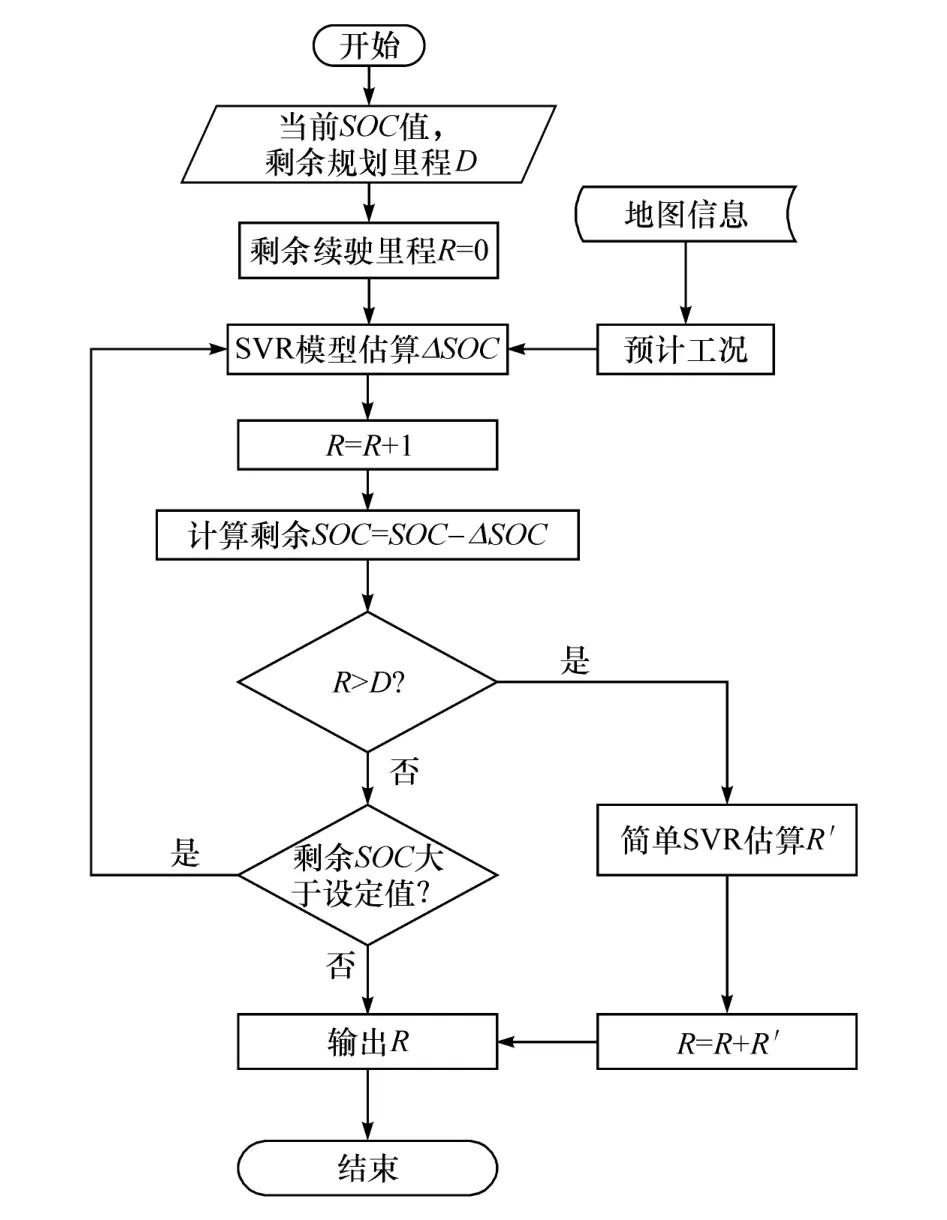
图7 循环SVR模型流程图

考虑到在行驶中汽车的剩余续驶里程R可能大于所规划路径的剩余里程D，此时没有地图信息对未来路况进行推测，且这种情况下续驶里程的估算结果一般不会引起驾驶员的里程焦虑，则此时可使用简单的SVR模型进行估计。简单SVR模型使用剩余SOC值、上一路段的平均工况参数和温度作为输入，剩余续驶里程作为输出，粗略估计汽车的剩余续驶里程R′，则最后的续驶里程为R＝R＋R′。

循环SVR模型中借助地图信息对汽车未来的行驶工况进行有效预测，能更加准确地估算出每公里SOC的变化，进而实现对续驶里程的精准预测。

4 仿真

结合ADVISOR软件和实际车辆行驶速度曲线设计仿真与实验。以某运输企业的车辆行驶数据为基础，提取实际行驶的速度曲线，将此速度载入到ADVISOR中用于模拟电动汽车在实际情况下的行驶过程。

由于目前对于续驶里程预测精度暂无公认的衡量指标，为评估模型在不同长度的行程下的预测精度，参考文献［11］，定义模型精度计算公式为

式中：A为预测精度；DT为实际行驶距离；RC为剩余续驶里程的变化（一段行程中两次剩余续驶里程预测结果的差值）。A越接近0则预测精度越高，且A＞0时，表示算法给出的剩余续驶里程比较保守，反之，如果A＜0，则说明给出的续驶里程偏高。

此外为衡量多次测试结果的平均精度，定义预测精度的绝对平均值E为

式中：Ai为第i次测试的预测精度；N为测试总次数。E越小表示模型的预测精度越高。

图8 车辆行驶速度曲线

以从数据抽取的一段行程为例，该段行程的起点是江西省吉安市井冈山市，终点是江西省南昌市西湖区沿江南大道。该行程的速度曲线如图8所示，车辆行驶路线如图9所示，行驶中各路段工况信息如表7所示。将此速度加载到ADVISOR中，使用EV1型电动车按照此速度完成这段里程的行驶，并在行驶中对剩余续驶里程进行估算。该段行程共计322.16 km，在仿真估算中剩余续驶里程由517下降为189 km，续驶里程变化328 km，A＝-0.0186。估算过程中车辆行驶里程、剩余续驶里程以及预测精度A的变化如图10所示。

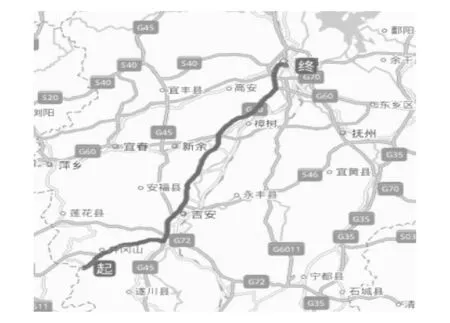
图9 车辆实际行驶路线

图10 车辆行驶里程、剩余续驶里程与预测精度A的变化

表7 行驶中各路段工况信息

为检验模型的精度，另从数据抽取20段行程进行测试，测试结果如表8所示，其中15段行程可以完成（即剩余续驶里程大于规划的里程），此时由于R＞D最终的估算较粗略，预测精度绝对值的均值为0.049 8。剩余5段里程未完成（R＜D，SOC降为0），预测精度绝对值的均值为0.018 2，与R＞D时相比更为精准。上述测试结果证明，该方法的预测精度在0.05以内，即每行驶100 km，续驶里程误差不超过5 km，能够为驾驶员提供较为可靠的指示，有效避免“里程焦虑”。

表8 20段行程测试结果

5 结论

剩余续驶里程在电动汽车驾驶中有着十分重要的指示作用。提出基于地图信息和循环SVR模型的纯电动汽车续驶里程预测方法。该方法借助于地图信息有效地降低了传统续驶里程估算方法中因未来工况未知对估算模型精度的影响。实验结果表明，该方法的预测精度在0.05以内，且A＞0的情况较多，实际行驶里程多大于系统给出的续驶里程，这能有效缓解驾驶员的“里程焦虑”。在车联网技术逐渐普及和不断发展的今天，路径规划和路况的获取也日益便捷和精准，该模型精度亦可随之提高。