基于RRT与MPC的智能车辆路径规划与跟踪控制研究*
2020-10-09过学迅裴晓飞余嘉星
周 维,过学迅,裴晓飞,张 震,余嘉星
(1.武汉理工大学,现代汽车零部件技术湖北省重点实验室,武汉 430070;2.武汉理工大学,汽车零部件技术湖北省协同创新中心,武汉 430070)
前言
智能车辆近年来是国内外汽车领域的研究热点,而局部路径规划和跟踪控制是其发展的关键技术之一[1]。其中,以RRT算法[2]为代表的采样规划算法,通过一个初始点作为根节点,采用随机采样的方式增加树结构的分支,当分支节点包含目标节点或进入目标区域,即可快速生成一条由树节点生成的从初始点到目标点的路径,具有概率完备性,在多障碍物的复杂场景应用较多。
针对传统RRT规划算法节点随机分布导致的计算时间长、规划路径完备且非最优、路径不平滑的问题,国内外学者提出了多种优化方法。文献[3]中提出了一种双向随机搜索树(Bi-RRT),从起始点和目标点同时向外拓展树结构,提高计算效率。文献[4]中指出合理的目标导向,可提高RRT求解速度。文献[5]和文献[6]中以Dijkstra算法和A*算法作为RRT的启发式函数,在搜索路径时以最小路径为参考,使规划结果更接近最优解。文献[7]中通过选择合理的度量函数节点,开发了连续曲率RRT(continues-curvature RRT,CC-RRT)路径规划方法。文献[8]中将RRT*与稀疏RRT(sparse-RRT)相结合,通过RRT*快速收敛于最优解的同时,利用修剪无用节点带来的稀疏特性减少计算量。文献[9]中首先用卷积神经网络训练预定场景下对应安全轨迹的期望加速度和转向角,然后将生成的控制输入加入RRT方法中完成状态空间的节点连接。仿真表明该方法在保证规划结果安全性的同时,提高了计算效率。
模型预测控制根据已知模型和当前状态量可估算输出,根据预测值与规划的期望值偏差,施加控制量输入,同时在控制过程中可施加多种约束,从而保证系统稳定、可靠地运行,因此在跟踪控制中得到广泛应用[10]。文献[11]中基于非线性MPC方案设计了智能车辆的主动转向系统,使车辆在预定轨迹跟踪时可保持稳定性,但该算法在速度大于10 m/s的情况下控制效果不佳,算法的实时性需要进一步提升。文献[12]中基于驾驶员意图识别和状态评估,设计了一种可完成避障路径的时变模型预测控制器,既可帮助驾驶员完成避障也可在不同工况下获得较好的车辆稳定性。文献[13]中通过实车试验证明基于非线性模型预测控制的轨迹跟踪能在高速结冰路面上成功避障。
集成合理且平滑的规划路径和鲁棒性较好的跟踪控制算法有助于提升智能车辆的综合性能,本文中通过目标导向、节点修剪、曲线平滑和最优路径选择的方法对传统RRT进行改进,以满足安全避障和运动学约束。针对车辆系统的强非线性和多模式约束,提出了集成LTV-MPC跟踪控制算法和改进RRT规划算法的智能车辆规划与控制算法,并以智能车辆的安全性和实时性作为评价指标,通过硬件在环仿真验证算法的合理性。考虑路径规划与跟踪控制算法的相互影响,分析了不同车速、规划步长、预测步长和控制步长对路径规划与跟踪控制效果的影响。
1 智能车分层构架
自动驾驶汽车主要由环境感知层、任务决策层、路径规划层和跟踪控制层构成,如图1所示。由环境感知层获知车辆的定位信息并构建可行驶区域,经由决策层形成全局路径,以全局路径为参考,路径规划完成局部环境下起始点到目标点最优路径的选择,该路径应连续、平滑、可避障并满足车辆运动学约束,以实现车辆的避障和连续平滑行驶的功能,跟踪控制模块接收路径规划的信号,自动调节油门、制动和转向等底层执行器,实现轨迹的平稳跟踪。
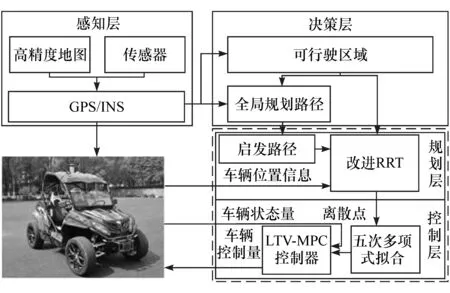
图1 智能车分层构架
本文中的主要工作集中于底层的路径规划和跟踪控制上,改进RRT规划算法根据全局路径和障碍物信息规划出一条平滑的局部路径后,跟踪控制模块接收来自规划层提供的参考轨迹点,通过LTV-MPC控制器计算出控制输入量,实现轨迹跟踪。
2 改进RRT路径规划算法
由于RRT算法的遍历特征,会导致生成的轨迹点具有不确定性、规划时间长、轨迹振荡剧烈和平滑性较差等不足。因此,提出了改进的RRT算法框架,如表1所示。表中:第6行,是采用目标导向的方法,改善基础RRT算法的随机性,减小单次规划所需的时间;第11行,是针对车辆行驶过程中应满足运动学和执行器不宜频繁操作的目标提出的节点修剪;第12行,为解决因节点修剪发生的振荡,引入路径平滑的方法;第13行,结合智能车辆的避障、稳定性和路径距离的要求,对基础RRT的规划算法制定了权重系数,引入最优路径选择的方法。

表1 改进快速搜索随机树算法框架
2.1 目标导向
基础RRT因概率完备,使得从起始点到目标点的收敛速度较慢,依据文献[4],本文中通过概率偏置和目标连接的方法进行引导随机树以提高计算效率。如表1中第4行,采样节点Sample-Point在概率小于一定值时,以目标点为随机点,可保证随机点的分布趋向于目标点。通过随机点分析出最接近点后,直接判断最接近点与目标点间的避障情况,减少规划次数,加速收敛。
2.2 最优路径选择
在目标点附近按照一定规律设置目标函数,可同时生成多条从起始点到目标点范围内的规划路径。以距离障碍物的位置、侧向加速度和路径长度作为评价指标,对可行轨迹进行选择,其判定方程为

式中:Lpath和Lmin分别为可供选择的路径长度和最短路径长度;dobstacle和dmin分别为各路径距离障碍物的距离和备选路径中距离障碍物最近距离;ay和amin分别为路径的侧向加速度和可行路径的最小侧向加速度;w1、w2和w3分别为距离障碍物位置、侧向加速度和路径长度的权重系数。为突出规划过程中对车辆避障和安全的考虑,在代价函数中提高车辆距离障碍物位置的权重,参照文献[14]的取值,w1、w2和w3分别取0.5、0.25和0.25。
2.3 节点修剪
如表1中第12行,采用贪心算法对最优路径上的节点进行修剪,以保证路径朝着最优路径逼近。改进RRT算法示意图如图2所示。由基础RRT可知从起始点到目标点会依次生成一系列点集,当其连线与障碍物有交集时,判定该点为碰撞点,进行规避,并重新规划,直到起始点与目标点进行连接,如图中实线所示。考虑实际车辆前轮转角约束,规划路径之间的夹角应尽可能平缓,仿真分析中设定路径的最小转角为90°[7],以a0点为起点,依次连接各规划点,以碰撞安全和最小转角为约束,修剪规划路径。对于夹角较小的规划路径,如图2中点a4所示,插入可平缓规划夹角的新点,直到抵达目标点。
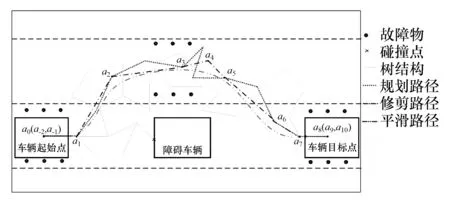
图2 改进RRT算法示意图
2.4 曲线平滑
由于车辆存在运动学约束,规划路径应满足曲线的2阶连续。考虑避障因素,节点的修改只影响局部曲线的改变,如图2中双点划线所示。综合规划路径的要求和计算成本,选择三次B样条曲线对路径进行平滑处理,三次B样条的矩阵表达式为
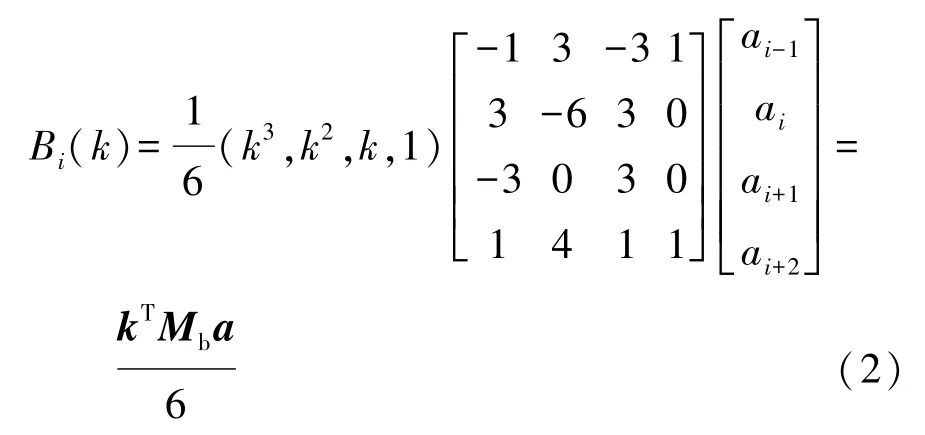
式中:Bi为第i段弧的B样条线解析式;k的取值范围为[0,1];ai、ai+1为内点。为了使拟合的曲线经过起始点和目标点,在a0的前面和an的后面分别增加两个节点a-2与a-1和an+1与an+2,以保证起始点和目标点处的运动学约束。
此外,改进RRT的规划周期和规划步长决定了路径规划的效果,规划步长过大,曲线拟合和避障效果变差,过小则对硬件的计算能力要求较高。
3 LTV-MPC轨迹跟踪控制算法
3.1 非线性轨迹跟踪模型
考虑单轨车辆的动力学模型作为MPC控制器的预测模型,采用线性轮胎模型,建立如下车辆动力学方程:

轨迹跟踪模型的输出为航向角φ和车辆质心的位置Y(或者包括质心的位置X),最终式(3)系统方程可表示为

3.2 LTV-MPC算法
利用Taylor线性化法建立基于LTV-MPC的轨迹跟踪控制器,相对于非线性模型预测控制中的用非线性规划求解优化问题,线性模型预测控制中采用的QP算法效率更高[9]。
3.2.1 线性时变状态方程
结合1阶Taylor展开式和雅可比矩阵,可对式(4)非线性状态方程在工作点附近进行线性化和离散化,为便于在约束条件中添加控制量增量约束,将状态方程写成增量形式,可推导出LTV-MPC的输出表达式:



式中:A(t)、B(t)、C(t)分别为动力学方程对状态量与控制量的导数和输出量对状态量的导数;Ak,t=T A(t)+I,Bk,t=T B(t),Ck,t=[C(t)0],T为离散时间间隔;Np、Nc分别为预测时域和控制时域;I为单位矩阵;dk,t为偏差项。
3.2.2 LTV-MPC代价函数及动力学约束
根据式(5)设计LTV-MPC代价函数,以保证自动驾驶汽车稳定、快速地跟踪期望轨迹,为了确保函数具有可行解,在目标方程中添加松弛因子,即LTV-MPC的代价函数为

式中:ρ为权重系数;ε为松弛因子。
由式(6)可知,LTV-MPC代价函数的解为控制增量,约束以控制增量或通过转换矩阵与控制增量乘积的形式出现。在车辆实际运行中,前轮转角和转角转速有一定限值,故控制量约束表达式为

式中:T1为Nc×Nc维的转换矩阵;Im为维度为m的单位矩阵;⊗表示克罗内克积;umin和umax分别为控制时域内的控制量最小值和最大值集合;ysc,min、ysc,max为软约束的极值。
为保证车辆处于线性区,参照文献[15]增加汽车质心侧偏角、车辆侧向加速度约束和轮胎侧偏角约束,即

式中:β为质心侧偏角;ay为车辆侧向加速度;μ为地面附着系数;af,t为轮胎侧偏角。
综上由式(5)~式(9)可知,影响跟踪控制效果的因素较多,如车速v、Np、Nc和权重系数Q与R等。
4 路径规划与跟踪的硬件在环验证
4.1 主要车型参数
在Simulink/CarSim联合仿真平台中,如图3所示,采用dSPACE RT1005模块进行实时仿真。首先,搭建智能车辆轨迹规划与跟踪控制系统的Simulink模型,然后通过自动代码生成模块加载相应的C代码,通过dSPACE/ControlDesk实现控制参数的实时调整,并完成车辆状态参数的在线观测和记录。图1中智能车的主要参数如表2所示,并在CarSim RT中进行相应设置。

图3 试验台架
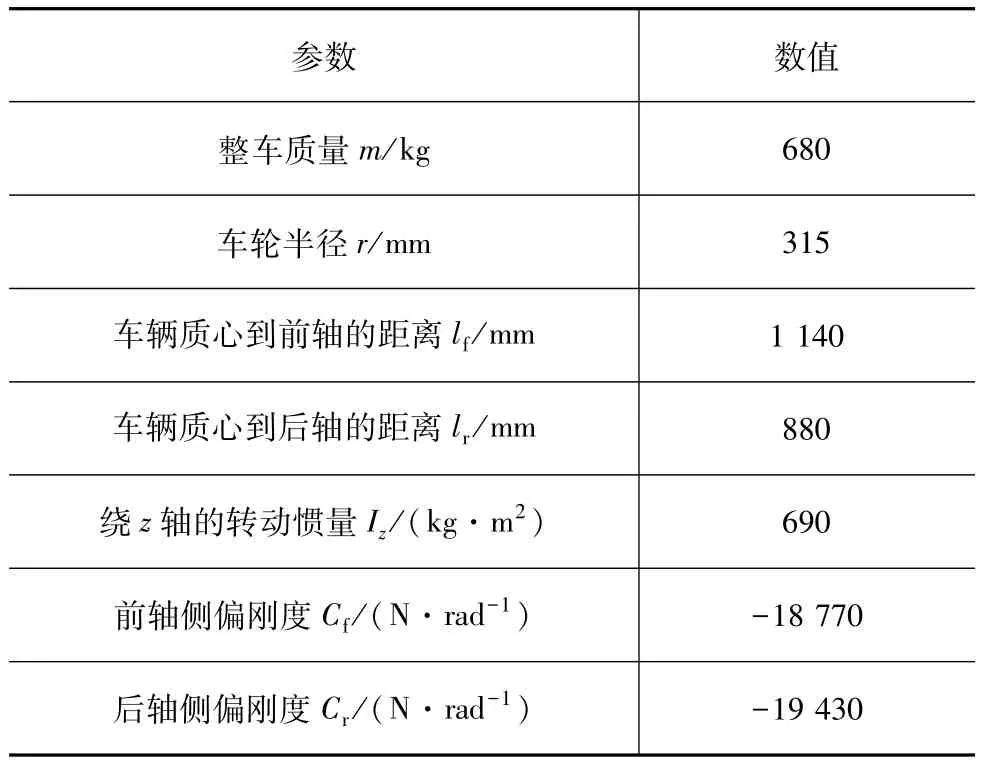
表2 智能车主要结构参数
4.2 离散点处理
在改进RRT的规划算法中,以全局路径为参考,结合环境信息规划出一条平滑的轨迹,并以离散点的形式传递给跟踪控制层。由于规划层和控制层的周期不一致,跟踪控制部分无法直接利用规划层提供的离散点数据,采用五次多项式拟合方法先将规划层得到的局部路径拟合成曲线,在控制层基于该曲线进行离散化,从而由时间域转化成几何域,消除周期不一致,实现规划层和控制层的顺利对接[15]。图4为规划路径与跟踪控制的联立图,其中虚线表示规划层离散点拟合曲线,控制层根据质心到曲线的最短路径计算车辆的输入控制增量,并进行跟踪控制。

图4 路径规划与路径跟踪的联立
4.3 仿真试验验证
基于ISO3888—1双移线试验工况,以道路中间线为规划与跟踪控制的启发路径。实时仿真采用的规划与控制器主要参数如表3所示,图5为智能车实时仿真结果。
由图5可知,基于启发式的引导路径,通过改进的RRT规划算法和LTV-MPC控制算法,可实现智能车的平稳行驶,图5(a)显示在移线过程中,智能车会出现偏离引导线,但最大横向误差小于0.7 m,最大横向偏差发生在拐角处,且在直线工况逐渐趋于稳定,在道路的边界线内可正常通过。图5(b)表示在智能车跟踪过程中,其最大的侧向加速度小于0.2g,航向角小于0.2 rad,满足稳定性约束要求。多次硬件在环仿真时长误差平均值为0.07 s,小于0.1 s,即小于单个的规划周期,说明提出的算法可实现路径的实时规划和稳定性跟踪。
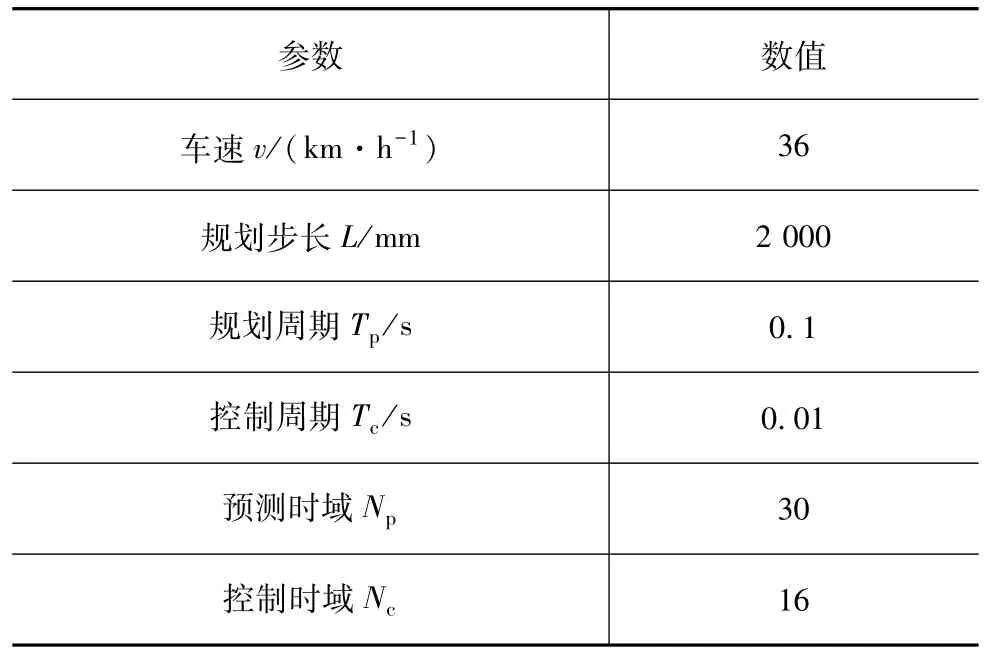
表3 智能车路径规划与跟踪算法主要参数
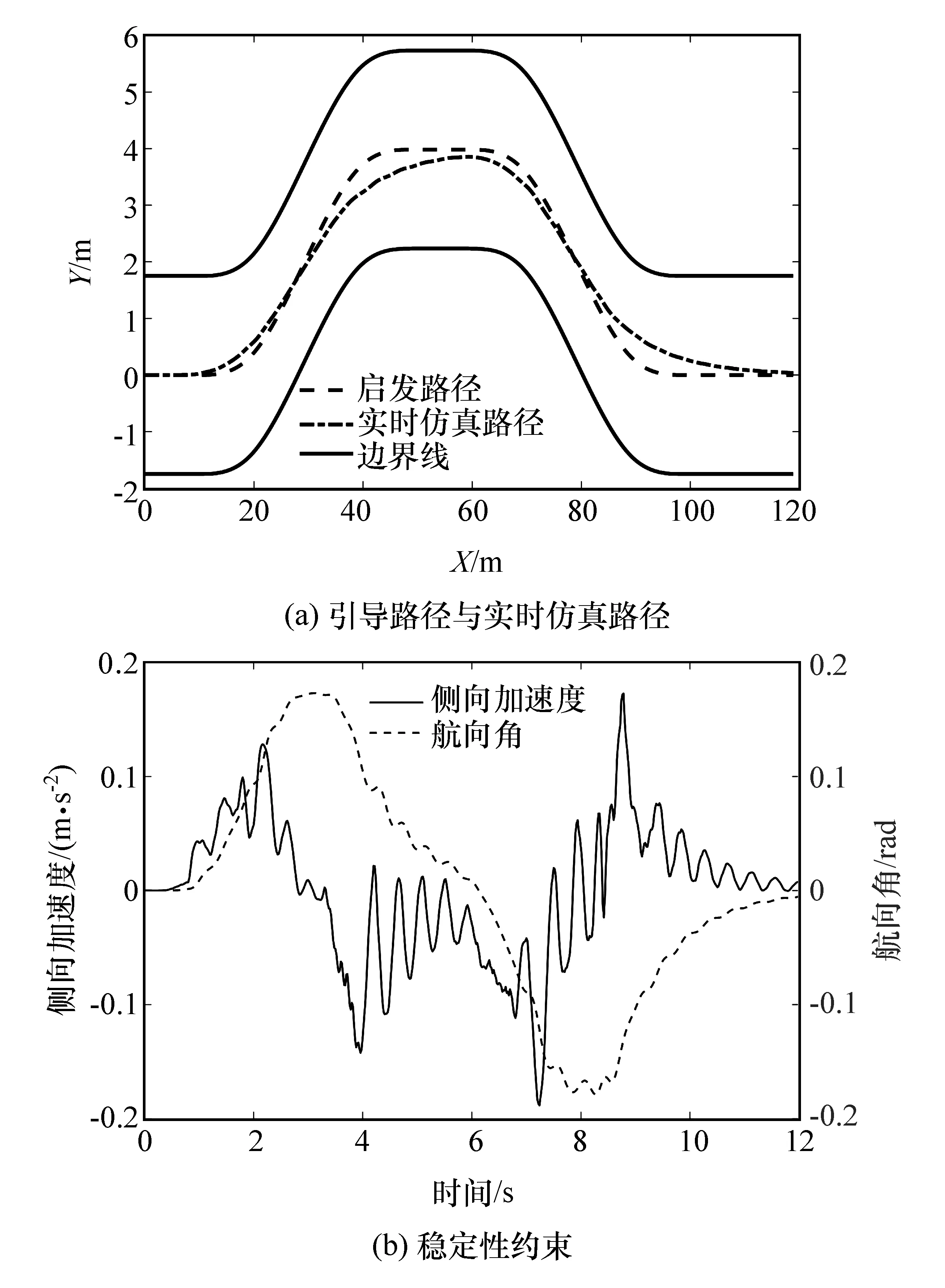
图5 智能车实时仿真结果
5 路径规划和跟踪效果的主要影响因素分析
由图5可知,虽然提出的改进RRT结合LTVMPC可实现智能车的实时规划和稳定性跟踪,但在移线拐点部分误差较大,须对其主要影响因素进行进一步分析。基于影响改进RRT和LTV-MPC算法的主要因素,文中以单移线试验工况为例,分析了不同车速、规划步长、规划周期对规划与跟踪效果的影响。
5.1 不同车速下的规划与跟踪效果
选取车速为18、24和36 km/h进行仿真,结果如图6所示。由图可见:在直线路径为启发路径时,不同车速的跟踪效果均较好;以转弯换道路径为启发路径,在一定速度范围内,速度越小,其跟踪的轨迹越接近目标路径。表4为不同车速下的最大侧向误差和最大航向角误差。

图6 不同车速下的仿真结果
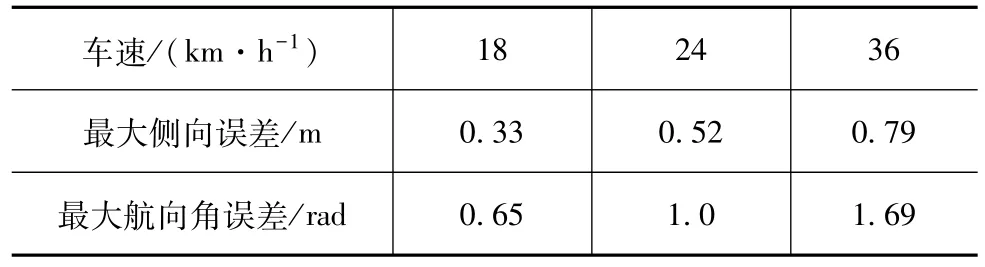
表4 不同车速下的最大侧向误差和航向角误差
5.2 不同规划步长下的规划与跟踪效果
规划步长为1 500、2 000和2 500 mm时的仿真结果如图7所示。由图可见,在换道转弯时,当速度达36 km/h时,规划步长为2 500 mm,其实际规划与跟踪的轨迹与目标轨迹的偏差较小。由文献[16]可知在U-turn工况,规划步长过长会对跟踪控制效果产生影响。同时由图2可知,RRT算法在规划算法较长时,容易出现拟合曲线和障碍物相交,故不宜选取过大的规划步长。表5列出了不同规划步长下最大侧向误差和最大航向角误差结果。

图7 不同规划步长下的仿真结果
5.3 不同规划周期下的规划与跟踪效果
考虑到车辆执行器的控制精度需求,选择控制周期为0.01 s,对于不同规划周期的跟踪和规划的效果如图8所示。由图可见,规划周期越长,其规划与跟踪的路径与目标路径越接近。因规划周期在一定范围内跟踪效果相近,且对于更短的规划周期,需要硬件提供更好的计算能力,因人类驾驶员规划周期为0.2~0.3 s,故一般选择稍快于人类驾驶员的0.2 s为规划周期。表6为不同规划周期下的最大侧向误差和最大航向角误差。
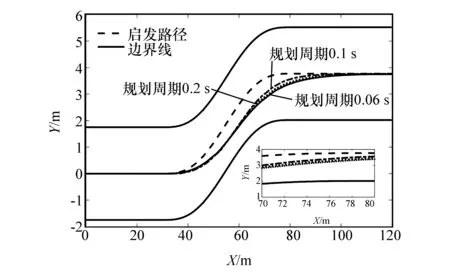
图8 不同规划周期下的仿真结果
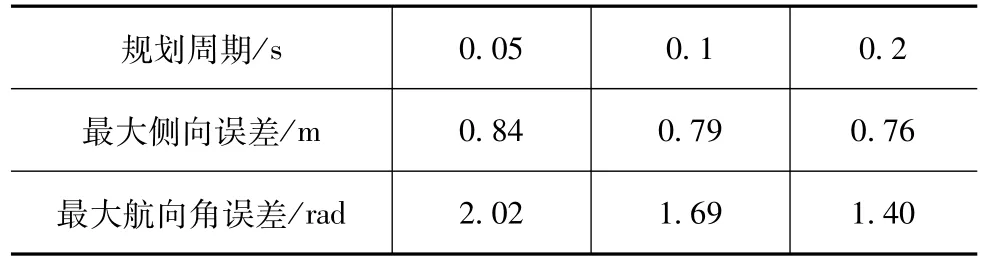
表6 不同规划周期最大侧向误差和航向角误差
6 结论
(1)本文中提出了一种基于改进RRT与LTVMPC的智能车辆路径规划与跟踪控制算法的基础构架,基于启发式路径,结合五次多项式对规划出的局部路径进行拟合,实现路径规划层和跟踪控制层的有效对接,硬件在环仿真验证了该智能车路径规划和跟踪算法的安全性和实时性。
(2)基于单移线试验工况,分析了不同车速、规划步长、预测步长和控制步长对规划和跟踪效果的影响。在一定的范围内,车速越小,规划步长越大,规划周期越大,规划和控制的轨迹与目标轨迹越接近。
(3)除了本文所讨论的规划与跟踪效果影响因素,执行器响应速率和控制器的计算能力等需进一步研究。此外,本文中仅通过硬件在环验证了算法的可行性,规划与跟踪的效果和实时性与稳定性也需进一步的实车试验进行验证。
