基于安全场改进RRT*算法的智能汽车路径规划方法*

朱 冰，韩嘉懿，赵 健，刘 帅，邓伟文

（1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022； 2.北京航空航天大学交通科学与工程学院，北京 100083）

前言

路径规划是智能汽车最为重要的核心技术之一，可根据宏观地图信息找到一条从初始位姿到目标位姿的连续无碰撞路径［1］。在实际道路环境中，智能汽车路径规划策略还须满足车辆动力学约束，同时具备较高的计算效率，及时规划出合理的期望路径。

快速搜索随机树（rapidly-exploring random tree，RRT）算法是解决路径规划问题的常用算法，它是一种基于均匀随机采样的增量式路径规划算法，具有概率完备性［2］。但RRT算法扩张效率低、路径抖动明显、易陷入局部区域，因此研究者提出了多种改进方案。

Xue等［3］借鉴人工势场思想，利用目标点和随机点作用于随机树上最近节点的“引力”矢量和来确定节点扩展方向，同时加入双向搜索策略，提高了算法的搜索效率。这类方法利用目标位置信息减少计算资源的浪费［4］，同时考虑了车辆的轨迹曲率约束。但是过度依赖目标点信息可能导致随机树在扩张过程中长时间陷入局部陷阱。冯来春等［5］提出结合A*算法和目标偏向策略引导随机树扩张，以使随机树的扩张更有指向性，从而提高搜索效率，但是需要额外建立栅格化地图。

Karaman等［6］将价值最低的相邻区域内的树节点作为父节点，在每次迭代过程中对该区域内的树节点重新连接，从而保证已生成路径总是较优的。Jeong等［7］提出的Q-RRT*算法在随机树新节点局部重构的过程中选取多级父节点进行比较，采用代价最低的节点作为新的父节点，从而使生成路径的长度更小。这些方法具有渐进最优性，但是计算量较大。

以上算法在避障处理时，大多采用判断新生成的随机树连接是否与障碍物存在交点的方式。如果没有交点意味不会发生碰撞，则接受该新节点并更新随机数。反之则撤销该连接。通过该方法可使随机树尽可能地在自由空间中探索，然而当障碍分布较为简单时，该方法效率较低，若能提前发现随机树扩张方向上的障碍物，然后据此规划避障路径，则能有效提高算法的计算效率［8］。为此，本文中提出一种利用安全场引导的改进RRT*算法，将安全场强作为选择节点的权重，使随机树的扩展方向能以足够大的概率指向远离障碍物的方向，提高收敛速度，减少计算量。

本文中首先根据实车驾驶数据建立了基于安全距离模型的安全场；在此基础上，提出具备安全场引导、角度约束等策略的改进RRT*算法；最后，通过离线仿真验证算法的有效性。

1 基于安全距离模型的安全场

1.1 安全场模型

驾驶人驾驶过程中避障意图的触发及减速跟车过程中的制动操作，均与车辆间的相对行驶状态以及驾驶人习性有关［9］，可引入“安全距离”对这一过程进行表征。所谓“安全距离”指后车通过采取一定强度的制动措施，使后车与前车等速并不发生碰撞所需要的初始相对距离［10］。对安全距离模型进行扩展，可得到能够定量评价行驶安全性的安全场模型。

车辆制动过程中减速度随时间变化的关系如图1所示［11］。

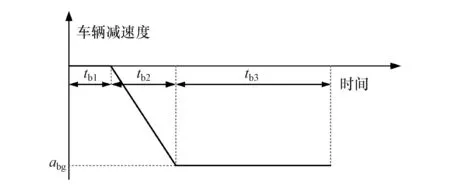
图1 制动过程车辆减速度变化曲线

图中：tb1表示驾驶人反应时间，期间主车制动减速度为0；tb2表示提高制动减速度的过程，期间制动减速度以斜率k线性升高直到设定的目标制动减速度abg；tb3表示制动减速度不变的制动维持过程，持续到与前车相对车速变为0为止。

为保证安全性，通常要求制动结束后两车之间要存有一定的安全距离裕度Sbs，可以得到主车开始制动时与前车之间应有的制动安全距离Sbw：

式中：Δv为开始制动时两车间相对速度；k为驾驶人正常行驶状态下的平均制动减速度变化率。k、Sbs和abg为模型参数，可通过实车驾驶数据分析提取得到。

据式（1），当两车相对距离下降到Sbw时开始以目标制动减速度abg制动，可实现前车留有距离裕度Sbs的避障状态。在紧急制动情况下，abg为接近路面附着条件允许的最大制动减速度，而在非紧急情况下，驾驶人通常以小于最大制动减速度的减速度进行制动。

将式（1）中的abg设为变量，依据驾驶人类型选定k值，则对于任意的abg，利用式（1）总能根据相对速度Δv计算出一个对应的临界制动安全距离Sbw。此时abg、Δv和Sbw3者的关系可用图2表示。

由图2可知，避撞制动时机主要与Δv和abg有关。因此用abg来表征行驶安全性，即某一强度的目标制动减速度会让驾驶员感到危机并造成速度损失，从而使其产生避障意图。

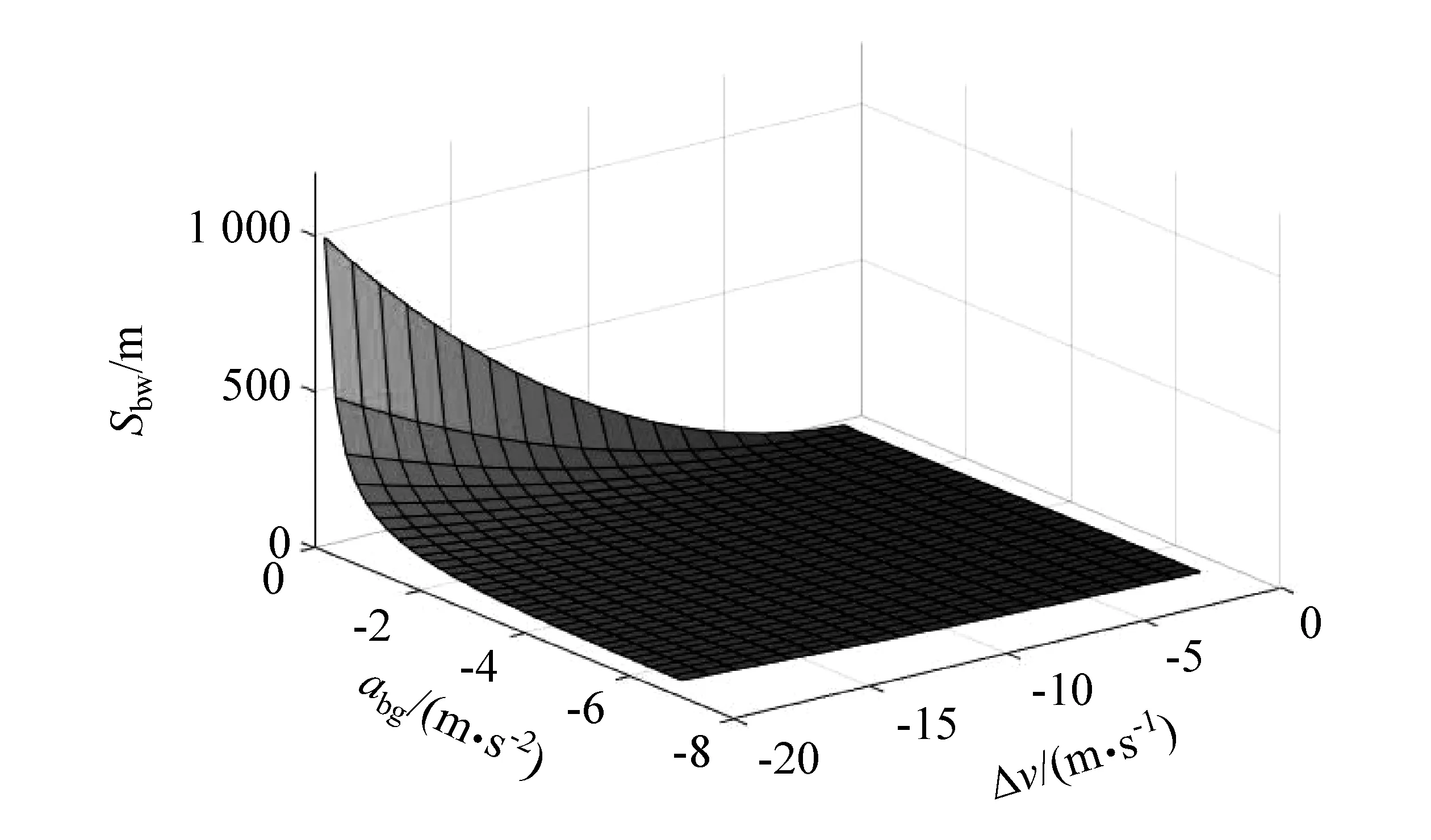
图2 安全距离模型

将式（1）中的Sbw和 Δv作为自变量，abg作为因变量，即得到安全场，如图3所示。图3反映了在一定的Δv和Sbw下主车避免碰撞所需的abg。可以看出，当相对距离缩小和相对速度增大时，主车所需采取的制动减速度增强，代表行驶安全性降低，该情况与实际驾驶经验相符。

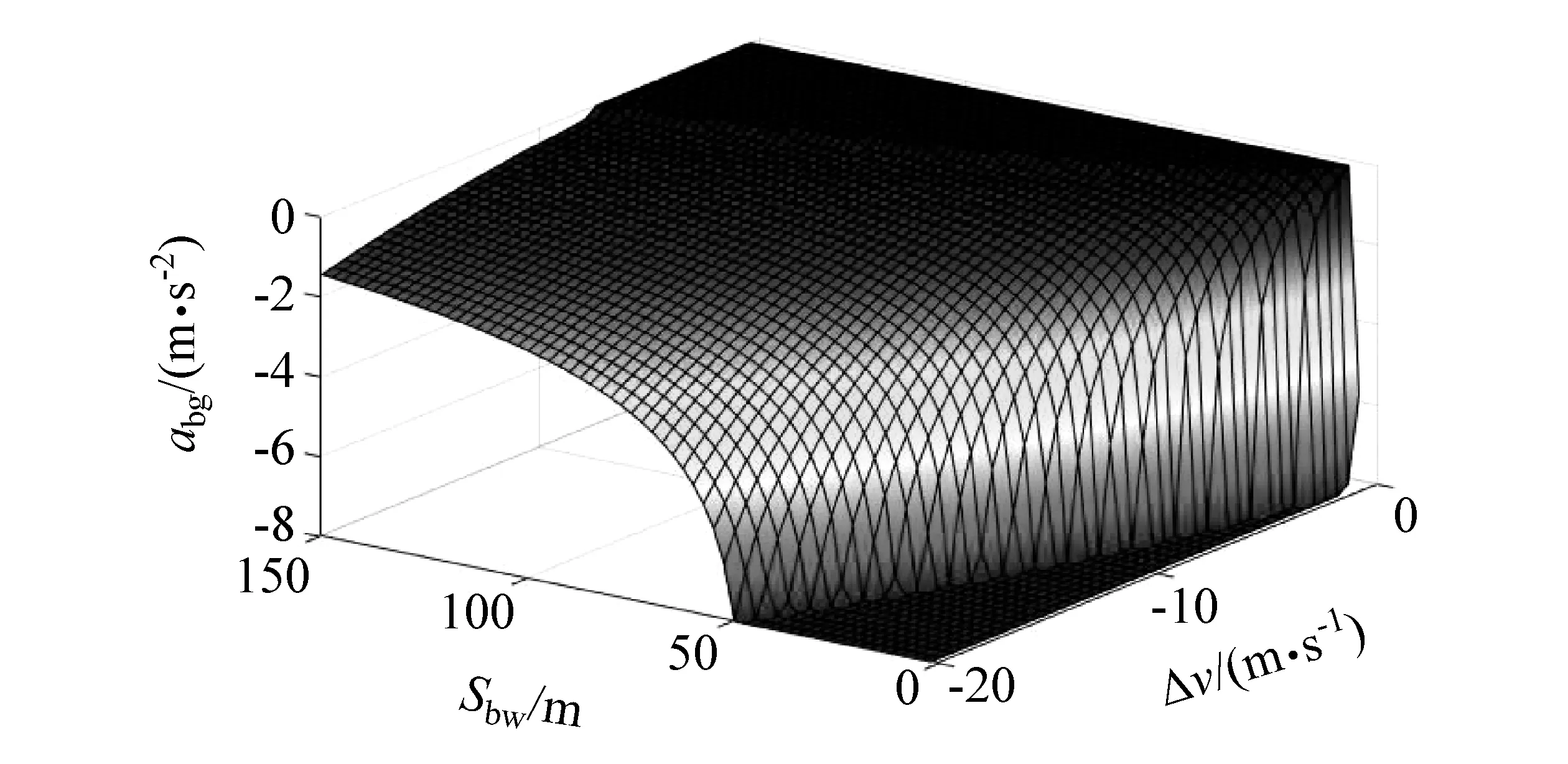
图3 安全场三维视图

为建立符合驾驶人习性、能反映车辆间行驶环境安全性的安全场，同时描述驾驶人对碰撞危险的敏感和接受程度，采用实车试验的方法采集驾驶人驾驶数据，在此基础上分析提取构建安全场所需的k、Sbs和abg3个参数。

1.2 驾驶人数据采集试验

搭建如图4所示的驾驶人驾驶数据采集平台，并设计了如表1所示的跟车和换道两种工况。其中vh0和vt0分别为主车和前车初始速度。跟车工况和换道工况可以反映出不同驾驶人对不同相对速度下安全距离的把握和减速制动过程中所采用的制动减速度。

平台主体由主车和交通车组成，两车各自搭载高精度惯性导航设备RT 3002／RT Range以及配套V2V和基站通信设备，连同车辆CAN总线数据可以获得包括车辆位置、速度和加速度在内的车辆状态信息。

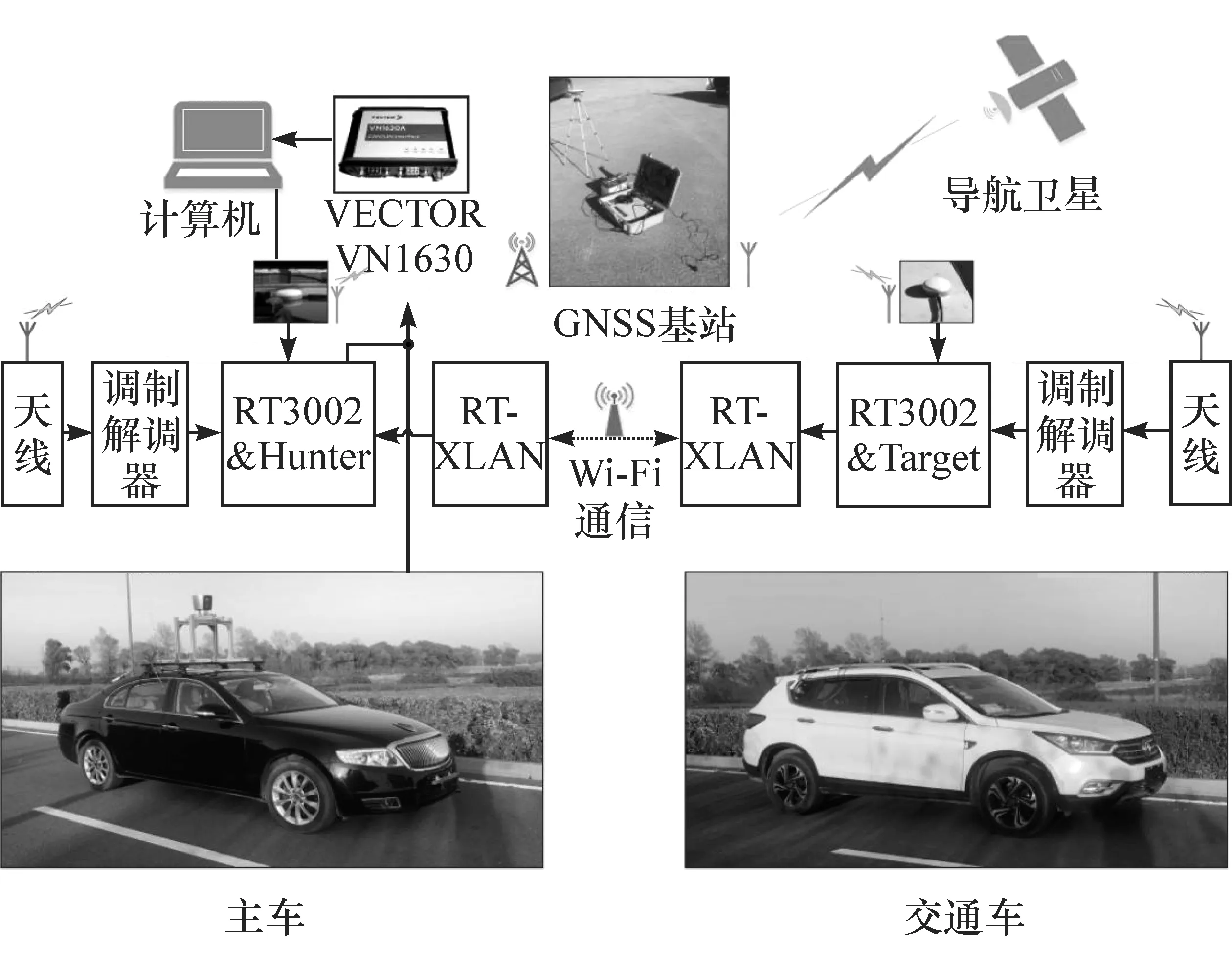
图4 驾驶人驾驶数据采集平台

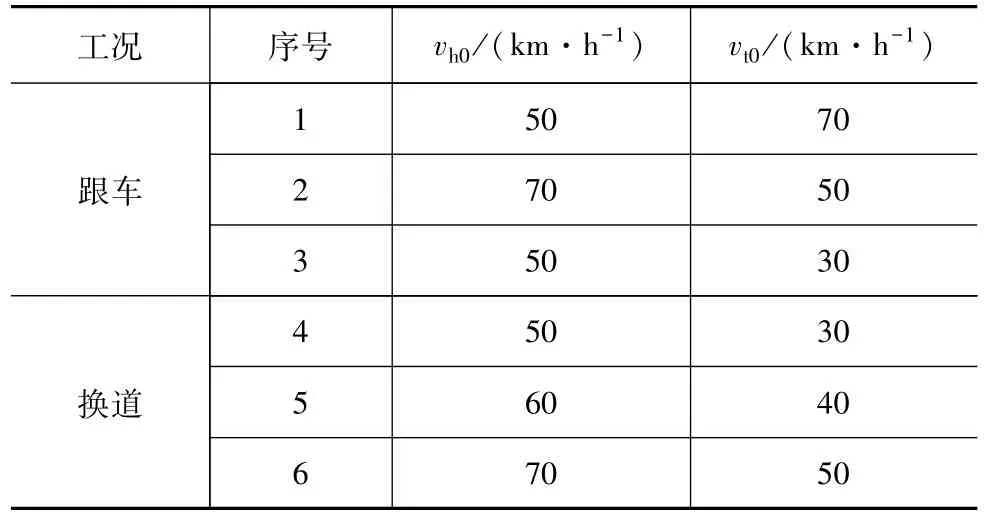
表1 驾驶人驾驶数据采集试验工况

跟车工况中，前车依据速度历程70→50→30 km／h行驶（在各阶段维持匀速），主车按照自身驾驶习惯跟车行驶。换道工况中，在两车产生一定距离后，主车以指定速度匀速追赶前车并在感知到前方低速车辆造成的潜在行驶危险时按照自身驾驶习惯切换车道避障。

试验共采集了87名驾驶人的数据。根据跟车工况驾驶人制动过程中的主车速度变化可以获取不同风格驾驶人习惯的车辆减速度；而换道工况中驾驶人换道开始时刻与前车的平均车间时距则能够反映出不同驾驶人对危险敏感程度的差异［12］。

根据实车试验数据进行聚类得到了3类不同风格驾驶人的安全场参数，实际应用过程中可以根据驾驶人驾驶风格选取对应参数，如表2所示。

表2 安全场参数

2 基于安全场改进RRT*算法

RRT算法［13］将初始点Pstart作为随机树T的父节点，然后通过迭代更新使新产生的节点Pnew与目标点Pgoal足够接近。迭代过程如下所述：在空间中随机生成点Prand，根据价值函数计算与Prand连接的节点代价值，将该值最小的点Pnearest选为父节点；从Pnearest向Prand延展出步长D获得新节点Pnew；判断Pnearest与Pnew的之间是否存在障碍物，若不存在，则在随机树上加入Pnew，反之则忽略Pnew，进行下一次迭代。

RRT*算法相较于RRT算法加入了新节点的父节点重选策略以及邻域内局部树节点的重构策略，使所生成的路径更加平滑，从而缩短路径长度［14］。RRT*算法具有概率完备性，无须事先对环境建立栅格地图，且可扩展性好，但该算法计算量大，盲目扩张策略导致计算资源的浪费，同时难以顾及终点的角度要求。因此本文中将安全场作为引导并加入角度约束策略对RRT*算法进行改进，使其能更好地应用于智能汽车路径规划。

2.1 角度约束策略

针对汽车航向约束，提出了一种新的节点扩展策略：设搜索空间中生成随机点Prand最近的节点为Pnearest，其父节点为Pparent。利用欧氏距离检索出距离Prand最近的点Pnearest，根据Pparent到Pnearest的矢量方向和范围［-θmax，θmax］按照式（2）和式（3）生成一系列点Pcan，i作为备选点集，再以安全场作为引导（在2.2节中介绍）从中选取一个点作为新的树节点。

式中：θi为点Pnearest到点Pcan，i的矢量与地图横轴的夹角；θnearest为点Pparent到点Pnearest的矢量与横轴的夹角；θcan，i为在［-θmax，θmax］内均布的第i个角度；θres为角分辨率；rand为0到1的随机数；floor表示向下取整；（xcan，i，ycan，i）为点Pcan，i的坐标；（xnearest，ynearest）为点Pnearest的坐标；D为扩展步长。

与先产生树节点、再通过角度约束筛选随机节点的方法不同，本策略在树节点生成时直接约束其扩展角度，使得每次迭代产生的树节点连接均满足曲率约束。此外，还能使路径符合起始点和目标点的角度约束。

2.2 安全场引导策略

依照驾驶人对障碍物的避撞倾向，利用前述构建的安全场，根据节点到障碍物之间的相对状态计算式（3）产生的一系列备选点的安全场强，将安全场强作为选择节点的权重系数，使随机树的扩展方向能以足够大的概率指向远离障碍物的方向，从而实现提前发现随机树延伸方向上的障碍物并据此规划避障路径，提升计算效率。

如图5所示，为便于说明，根据式（3）在θnearest的［-θmax，θmax］内产生了3个备选点，记为Pcan，i，i∈｛1，2，3｝。以Pnearest为端点，向Pcan，i作射线。当前方存在障碍物时，可得到备选点沿射线方向到障碍物的距离Sbw，i。根据主车速度得到相对障碍物的速度Δv。在此基础上即可利用前述安全场得出临界制动减速度abg，i，即为安全场强。安全场强越大（绝对值）代表由该备选点所产生的路径安全性越低，该备选点被选取的概率越应降低。图5中距离Sbw，3最大，计算得出的安全场最低，因而Pcan，3被选定为新树节点的概率最大，引导随机树绕开障碍物。

图5 安全场引导策略

安全场强表示可能路径上的碰撞风险，当存在多重障碍物导致场景较为复杂时，若单纯地按照安全场强选择最安全的节点可能会导致错失最短的连通路径。因此在兼顾避障能力的基础上，通过概率选点的方法保留对安全场强较低区域的探索能力。以均值μ为0，方差σ为abg的方差，按照3σ原则设置饱和上限。采用式（4）计算权重wcan，i。利用式（5）对备选点Pcan，i的权重wcan，i做归一化得到该点被选为树节点的概率pcan，i，其中N为备选点数。

将全部备选点按照其概率大小作为区间长度顺序排布在［0，1］范围内，然后生成一个［0，1］范围内的随机数，该随机数所处区间的所属备选点即被选作为新树节点。

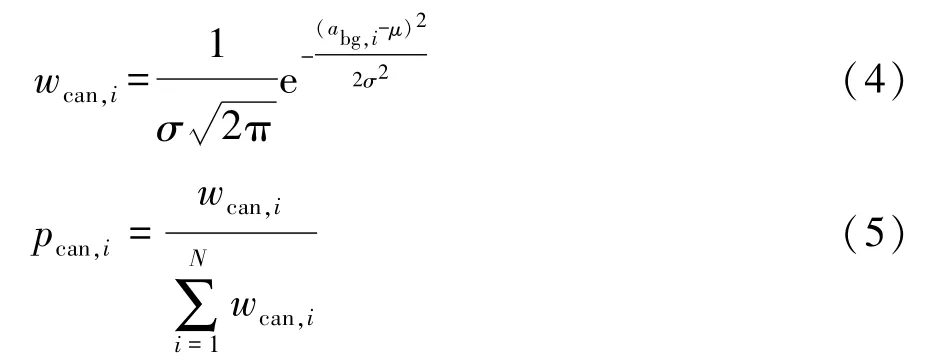
以图5的场景为例，障碍物垂直于X轴，Pnearest到障碍物的距离为40 m，Pparent到Pnearest的矢量与X轴夹角为345°，θmax设为45°，θres设为3°。车速为30 km／h。按上述方法计算得到各位角度处备选点的概率，如图6所示。备选节点所处半径越大代表概率越大。

图6 备选节点的被选概率与节点延伸方向的关系

在约束角度［0°，30°］∪［300°，0°）范围内，避障潜能越高的备选点的被选定概率越高，因此有助于降低算法在障碍物周围区域的无效扩张，提高算法效率。

综上，安全场引导改进RRT*算法流程如图7所示。当算法生成连接起点和目标点的路径后，可以通过剪枝和五次B样条曲线进行处理得到最终轨迹［15］。

图7 算法流程图

3 仿真试验

为验证本文提出的安全场改进RRT*算法，设计了两种工况，并在加入贪婪策略的情况下对RRT、RRT*和改进RRT*在600 m×600 m的场景地图内分别进行了20次仿真试验。其中，安全场改进RRT*采用表2中一般型驾驶人数据作为安全场参数。

3.1 单个障碍物场景

在起始点（圆点，坐标（100，300），航向0°）和目标点（星形，坐标（500，300），航向90°）之间设置垂直于横轴的单个狭长障碍物对算法的避障能力进行测试。仿真得到的路径规划结果和统计结果分别如图8和表3所示。

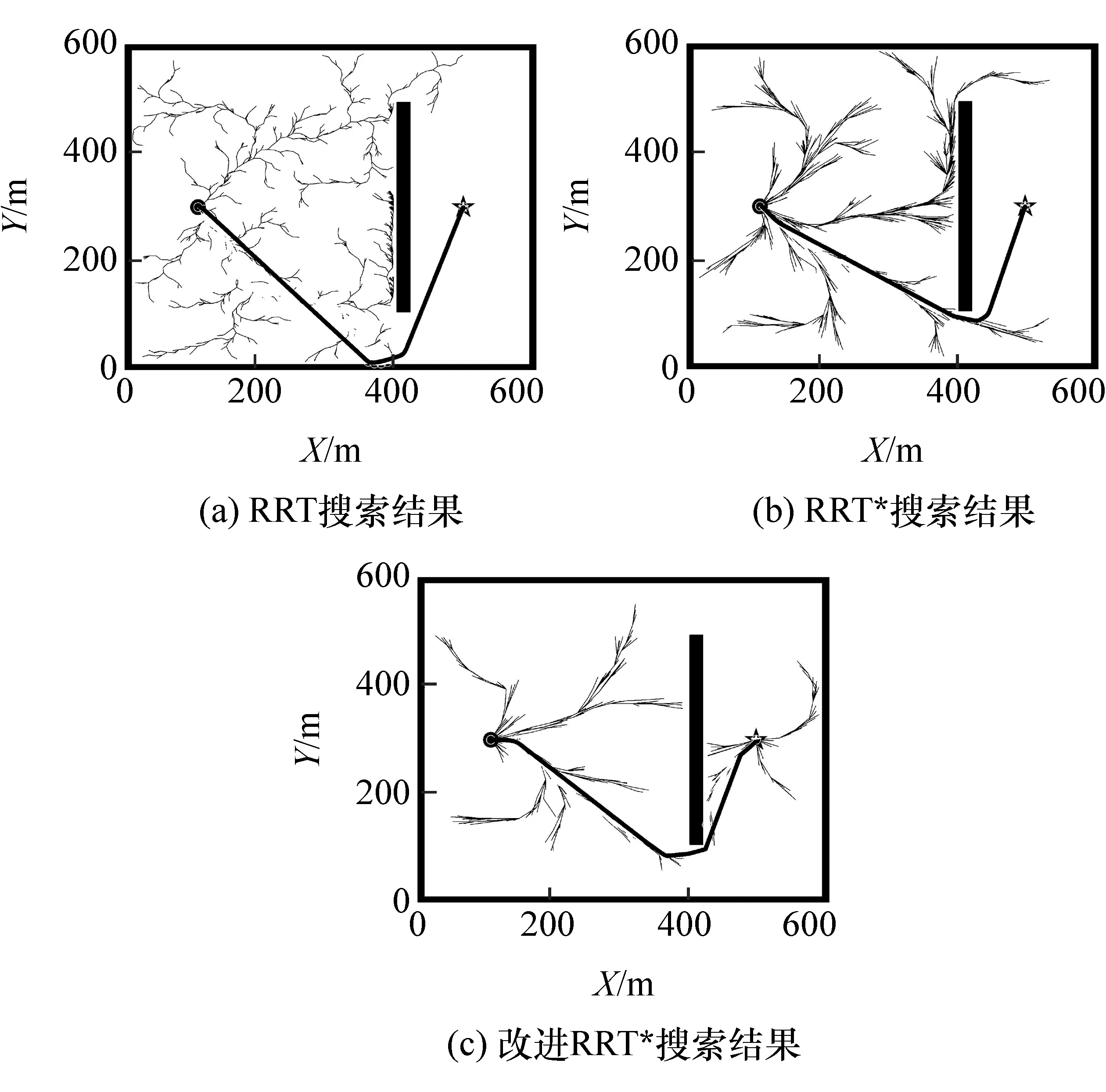
图8 工况1仿真结果图

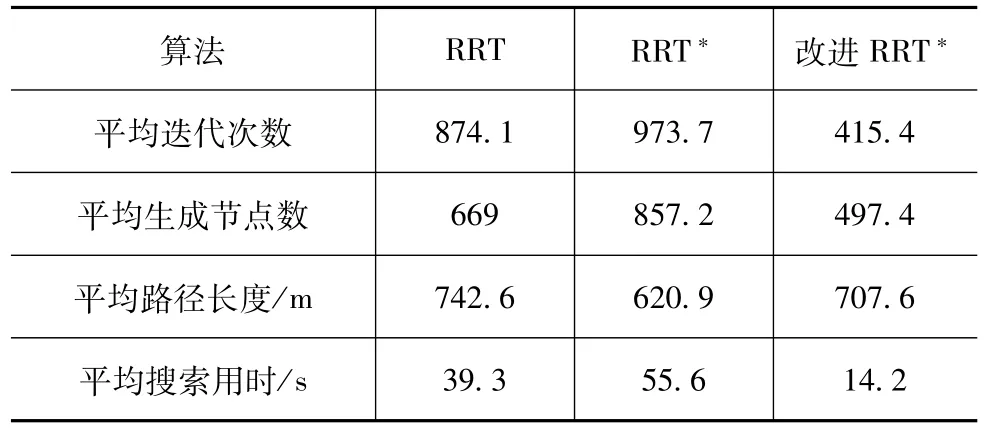
表3 工况1仿真结果统计数据

图8中分别为RRT、RRT*和改进RRT*在场景地图中生成的原始路径，黑色粗实线为经过平滑处理后得到的路径。由图8（a）可以看出，RRT在起始点附近的空间内扩展出大量的节点，当接近障碍物时，在其左侧生成了大量分枝，经过了大量迭代次数才成功连通至障碍物右侧，整体收敛速度慢。RRT*产生的路径较RRT平顺并且也更短，但RRT*附加的策略增加了每次迭代中的计算量，如表3所示，RRT*相较于RRT耗费更多时间进行搜索。

本文中提出的改进RRT*利用安全场引导并借助角度约束策略，使得随机数上的大部分节点提前绕行了障碍物并保证了路径平滑。从表3中可以看出，该方法在平均迭代次数、算法生成节点数和搜索用时上均优于另外两种算法。综上所述，对于单个障碍物场景，在3种算法均能够规划出可行路径的基础上，本文中提出的改进RRT*效率更高。

3.2 多重障碍物场景

通过在地图中摆放多种障碍物形成包含狭窄通道，局部小区域和大转弯在内的场景。设定起始点（圆点，坐标（150，75），航向180°）和目标点（星形，坐标（450，75），航向180°）。图9所示为RRT和RRT*的规划路径。两种方法在20次试验中均未能在迭代3 000次内成功规划出路径。

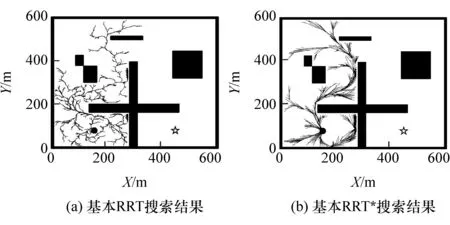
图9 RRT和RRT*仿真结果图

图10 改进RRT*算法仿真结果图

图10所示为改进RRT*算法成功规划出的路径。在20次试验中共有14次在迭代3 000次内成功搜索出路径，成功率达70%。统计结果如表4所示，平均迭代次数为1 575.3次，远小于给定的3 000次。与RRT和RRT*相比，本文中提出的改进RRT*扩展效率较高，在搜索时借助安全场实现了提前避障的能力，可较快地规划出路径。同时，在多次仿真中计算出了多种路径，表明算法在提高了规划速度和成功率的同时保留了较好的空间探索能力。

表4 工况2仿真结果统计数据

综上所述，本文中提出的基于安全场的改进RRT*算法能够以更高的成功率快速地规划出满足轨迹曲率约束的路径。

4 结论

本文中针对RRT算法和RRT*算法计算效率低、对车辆角度约束满足性差以及易陷入局部区域等问题，提出了一种基于安全场改进RRT*算法的路径规划方法。首先建立了安全场模型，并通过实车驾驶数据采集与分析，获取了安全场参数；随后通过加入角度约束和安全场引导策略，提出了改进RRT*算法；最后，通过对RRT、RRT*和改进RRT*进行对比测试，验证了本文中提出的路径规划方法具备生成满足航向角约束的平滑路径的能力，同时在搜索效率和成功率方面有着明显优势。