基于NSGA-Ⅱ的主动式安全气囊参数优化*

葛如海，崔义忠，洪 亮，肖 轩

（1.江苏大学汽车与交通工程学院，镇江 212013； 2.常熟理工学院，常熟 215500）

前言

目前，我国中小学生的数量已接近2亿，校车的潜在需求量超过120万辆，但我国校车保有量仅达到校车潜在需求量的1／4［1］。正规校车数量无法满足市场的需求，以及大量乡村学校的取缔合并，催生用于接送中小学生的非法营运车辆。校车安全法律法规的不完善以及非法营运屡禁不止，导致全国校车事故频发且部分事故儿童乘员的死亡率高达80%［2］。

我国于2012年正式颁布校车标准GB24407《专用校车安全技术条件》［3］。该标准规定校车使用的儿童乘员用约束装置是两点式安全带。研究表明，两点式安全带仅能约束儿童乘员的腰腹部，对头部、颈部和胸部的保护效果不佳［4］。三点式安全带的正确使用能减少儿童乘员的损伤，但三点式安全带是针对成年乘员设计的，儿童乘员与成年乘员的身材尺寸存在较大差异，导致三点式安全带的误作用现象十分严重，三点式安全带的误作用不仅不能提高儿童乘员的碰撞安全性，还会对儿童乘员的颈部造成致命损伤［5］。

为进一步提高校车乘员约束系统对儿童乘员的保护效果，文献［6］～文献［8］中提出一种应用于校车的主动式安全气囊，该种气囊在校车行驶的过程中始终保持开启的状态，当发生碰撞时通过气囊袋的弹性变形以及排气孔的空气阻尼作用吸收儿童乘员的碰撞能量。本文中在此基础上研究主动式安全气囊控制参数对6岁儿童乘员的损伤影响，同时利用非支配遗传算法（NSGA-Ⅱ）进行优化分析。

1 校车约束系统的建立与验证

1.1 校车约束模型建立

以国内某款校车作为校车原型建立校车仿真模型，因校车乘员约束系统仿真中与儿童乘员可能发生接触的部件以及台车试验中涉及的部件均是地板、前后排座椅（包含坐垫和靠背），故本文中建立的校车约束系统模型简化为前后排座椅、地板和两点式安全带。仿真使用的假人按照标准GB27887《机动车儿童乘员用约束系统》选取HybridⅢ6岁儿童假人。校车乘员约束系统模型如图1所示。

图1 校车乘员约束系统模型

通过碰撞速度为30～32 km／h台车碰撞试验［9］与仿真的部分损伤指标曲线的一致性、不同时刻的运动姿态的一致性以及损伤指标的误差范围，验证校车模型的正确性。损伤曲线如图2所示，运动姿态对比如图3所示，损伤指标误差对比如表1所示。

图2 仿真模型验证曲线

图3 运动姿态对比图

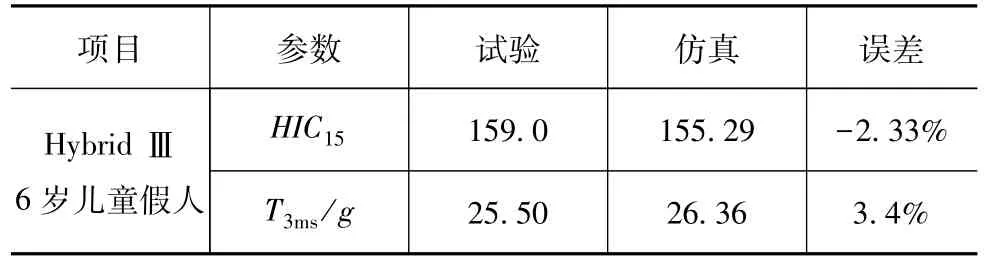
表1 仿真与台车试验损伤指标结果对比

由图2可知，台车试验与仿真的头部合成加速度和胸部合成加速度曲线在“开始时刻、基本形状、响应峰值以及峰值时间”特征均保持较高的一致性。由图3可知，在0、50和150 ms 3个时刻，台车试验的假人运动姿态与仿真模型假人的运动姿态具备较高的相似性。由表1可知，6岁儿童乘员的头部损伤指标值HIC15和胸部3 ms合成加速度T3ms的台车试验与仿真之间误差均在4%以内，表明校车模型能较为准确地再现台车试验的试验结果。

1.2 主动式安全气囊模型

主动式安全气囊是通过CATIA建立三维模型，然后利用Hypermesh进行网格划分，网格选用的是三角形膜单元，通过控制网格质量参数雅格比、翘曲和单元尺寸提高网格质量，然后将主动式安全气囊的网格模型导入MADYMO中调整尺寸比例和定义接触，形成主动式安全气囊MADYMO模型，如图4所示。最后进行仿真分析，分析结果如表2所示。

图4 主动式安全气囊模型

表2 有无主动式安全气囊的儿童乘员损伤值对比

由表2可知，主动式安全气囊使6岁儿童乘员的头部损伤指标HIC15减小了16.2%以上，颈部损伤指标Nij减小了29.3%，左右大腿的轴向力（FFCL、FFCR）分别下降10.59%和21.05%。由此可见，主动式安全气囊能进一步减少校车儿童乘员的损伤情况。

2 主动式安全气囊控制参数对6岁儿童损伤的影响

主动式安全气囊对儿童乘员损伤产生影响的参数主要为气囊包形、气囊安装位置、气体质量流率和排气孔开度与开启压力，以及主动式安全气囊与儿童乘员的距离。故本文中研究拉带长度、气体质量流率、气囊安装位置、排气孔开度、气囊初始压力、排气起始压力以及座间距等7个参数对6岁儿童乘员的保护效果。

2.1 拉带长度

拉带长度调整主动式安全气囊的包形，改变6岁儿童乘员头部和颈部与气囊接触位置的厚度。拉带长度的设计原值为235 mm，以设计原值为中心在205～265 mm之间选择7组数据进行仿真分析，研究不同拉带长度对6岁儿童乘员的损伤情况。6岁儿童乘员的损伤指标如表3所示。

表3 拉带长度对儿童乘员的保护效果

2.2 气体质量流率

气体质量流率对气囊的充气和排气过程均存在影响。在充气过程中，气体质量流率影响气囊充气完成时的初期内部压力；在排气过程中，气体质量流率会影响气囊内部压力的变化速率，对儿童乘员的保护作用产生重要的影响。在气体质量流率设计值的80%～125%的范围内选择7组数据进行仿真分析，研究气体质量流率对6岁儿童乘员保护效果的影响。6岁儿童乘员的损伤值如表4所示。

2.3 气囊安装位置

气囊安装位置是指气囊安装点距前排坐垫上表面的垂直距离，且气囊初始位置距离前排坐垫上表面0.395 m。气囊安装点位置示意简图如图5所示。

本文中将0.395 m作为设计原值，并以设计原值为中心在0.345～0.41 m范围内选择7组数据研究气囊安装位置对6岁儿童乘员的损伤影响。6岁儿童乘员的损伤值如表5所示。

2.4 排气孔开度

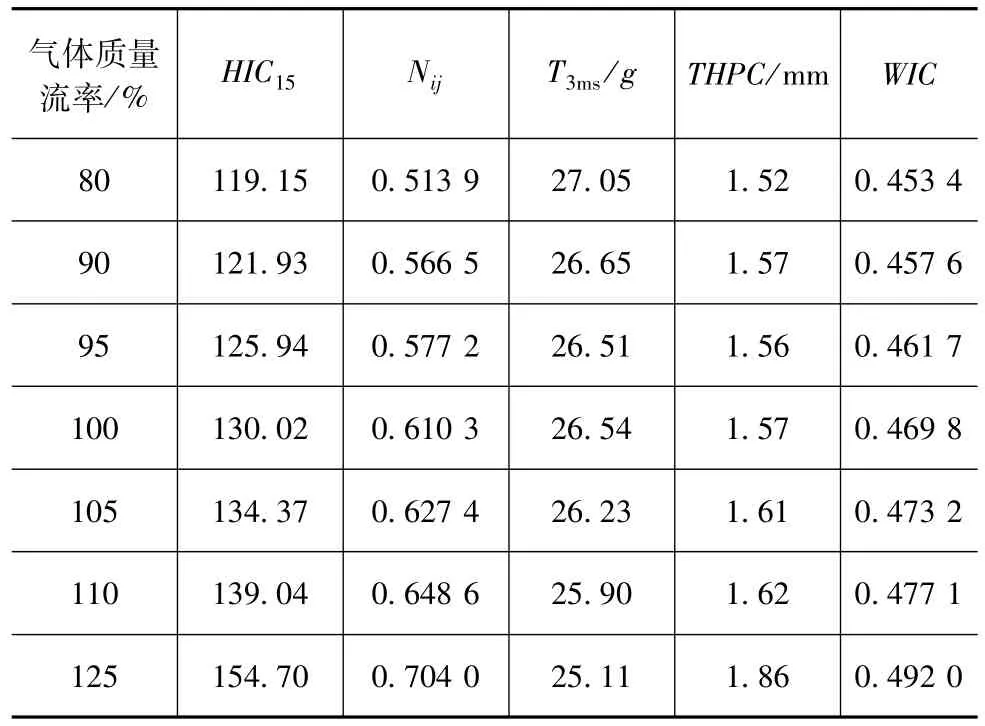
表4 气体质量流率对儿童乘员的保护效果

图5 气囊安装点示意简图

表5 气囊安装位置对儿童乘员的保护效果

排气孔开度与气囊内部气体泄漏快慢有关。气囊排气过快，6岁儿童乘员易击穿气囊与前排座椅直接接触，造成更大的损伤。如果排气速度过慢，气囊内部压力过大，使主动式安全气囊发生刚化，增加儿童乘员的损伤情况。在排气孔开度设计值的80%～200%的范围内选择7组数据，研究排气孔开度对6岁儿童乘员损伤情况的影响。6岁儿童乘员的损伤情况如表6所示。

2.5 气囊初始压力

气囊初始压力是指气囊在充气过程结束后气囊内部的压力值。气囊初始压力的设计初值为1.1092×105Pa，以设计初值为中心在1.105×105～1.1134×105Pa之间选择7组数据研究气囊初始压力对儿童乘员的损伤影响。6岁儿童乘员的损伤情况如表7所示。

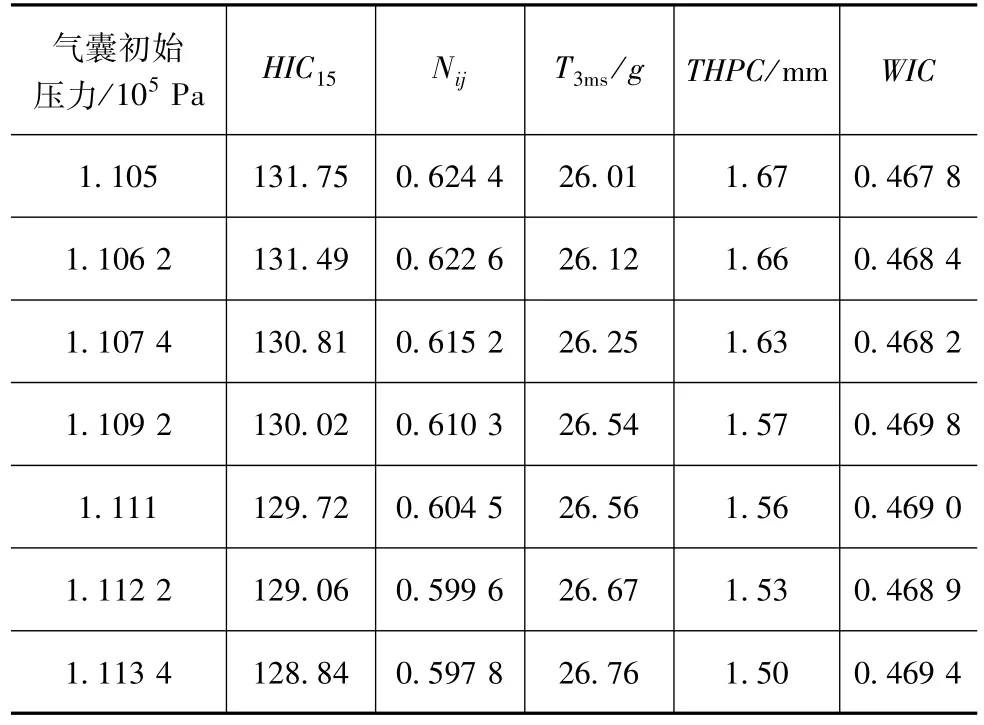
表7 气囊初始压力对儿童乘员的保护效果

2.6 排气起始压力

排气起始压力对气囊是否发生刚化现象起决定作用，因此如何选择排气起始压力对主动式安全气囊的保护效果具有重要影响。排气起始压力的设计初值为1.25×105Pa，以设计初值为中心在1.16×105～1.29×105Pa范围内选择7组数据研究排气起始压力对6岁儿童乘员损伤情况的影响。6岁儿童乘员的损伤情况如表8所示。

2.7 座间距

座间距改变主动式安全气囊与儿童乘员之间的距离，改变了主动式安全气囊与两点式安全带的能量吸收的比例。座间距的设计初始值为0.7 m，按照法规GB24407要求座间距须大于0.65 m，故以设计初始值为中心，在0.65～0.75 m之间选择7组数据评价座间距对儿童乘员保护效果的影响。6岁儿童乘员的损伤情况如表9所示。

3 参数灵敏度分析

通过灵敏度分析方法筛选出对儿童乘员保护效果影响较大的参数进行进一步的优化分析。灵敏度计算公式为

灵敏度越大，控制参数对WIC值影响越大。主动式安全气囊控制参数对WIC值的影响如图6所示。

由图6可知，对综合损伤指标WIC影响较大的参数是拉带长度、排气孔开度、排气起始压力和座间距，灵敏度分别为10.06%、13.28%、16.54%和18.30%；对颈部损伤指标Nij影响较大的参数为拉带长度、气体质量流率、排气孔开度、排气起始压力和座间距，灵敏度分别为11.04%、15.79%、14.82%、15.43%和10.56%。

图6 灵敏度分析

4 基于NSGA-Ⅱ的参数优化

4.1 设计变量与设计目标

由上述灵敏度分析可知，同时对WIC和Nij存在较大影响的参数为拉带长度、排气孔开度、排气起始压力和座间距，取值范围如表10所示。因此本文中将拉带长度、排气孔开度、排气起始压力和座间距作为设计变量进行主动式安全气囊的优化分析。

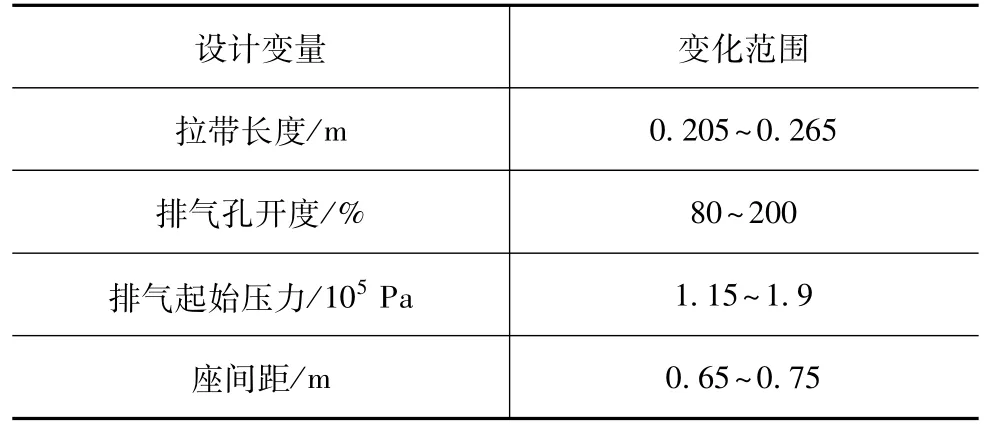
表10 设计变量的变化范围

本文中将综合损伤指标WIC［10-11］和颈部损伤指标Nij［12］作为设计目标进行关键参数的优化分析。

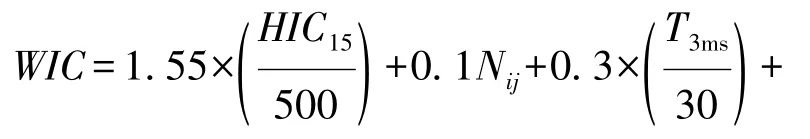
式中：HIC15为头部损伤指标HIC在15 ms时间间隔的测量值；T3ms为胸部3 ms合成加速度；FFCL、FFCR分别为左右大腿骨最大轴向力。

式中：Fz为颈部轴向力；Fzc为颈部轴向力的耐受极限值；My为颈部弯矩；Myc为颈部弯矩耐受极限值。

4.2 拉丁超立方试验设计

拉丁超立方（Latin Hypercube）试验设计是基于随机抽样的试验设计方法［13］，该方法将每个因子的设计空间都均匀划分开（即所有因子均具备相同数量的分区），然后将这些水平值随机的组合，再通过优化准则保证样本点的均匀性。

本文中共设计14次试验，试验设计及其仿真结果如表11所示。

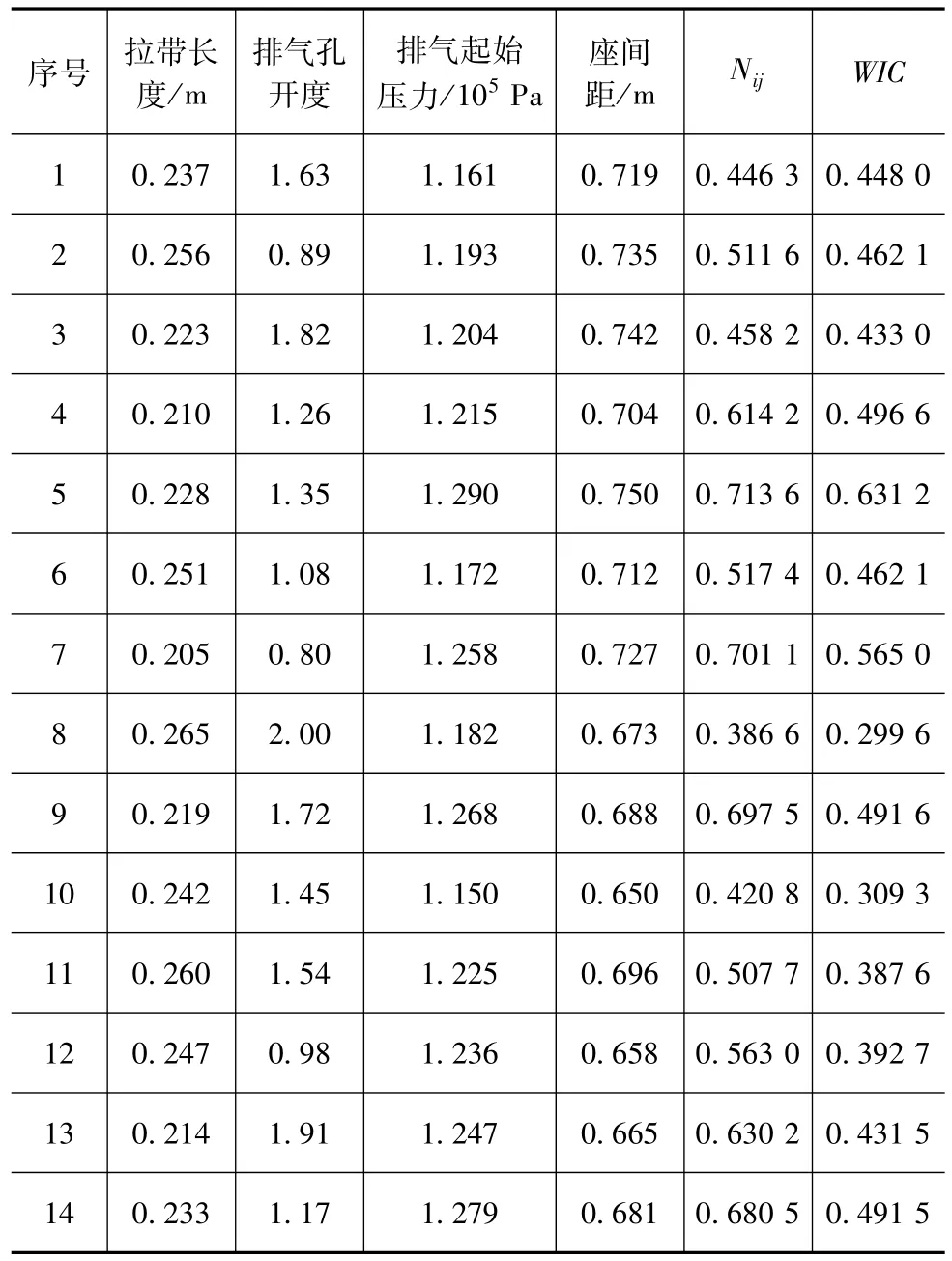
表11 优化变量的试验设计值

4.3 多项式响应面模型

结合上述设计试验，通过构建2阶响应面模型来研究WIC和Nij与拉带长度、排气孔开度、排气起始压力和座间距之间的关系。2阶多项式响应面的基本形式［14］为

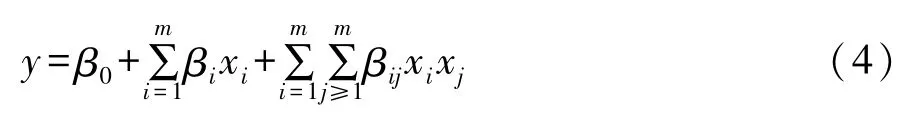
式中：y为响应面拟合函数；x1，x2，x3，…，xm为设计变量；m为设计变量个数；β为待定系数。

利用方差分析中的决定系数R2验证模型精度。

式中：yi为响应变量的仿真值为响应变量的预测值为响应变量仿真值的平均值。

基于上述仿真结果获得的WIC和Nij以及多项式响应面模型的原理，求解获得WIC和Nij与拉带长度、排气孔开度、排气起始压力和座间距等4个变量的2阶多项式响应面模型，其表达式为

式中：x1为拉带长度；x2为排气孔开度；x3为排气起始压力；x4为座间距。

WIC的决定系数R2为0.989 4，Nij的决定系数R2为0.996 9。为验证上述表达式的正确性，随机选择5组样本点进行检验。表12为选取样本点与检验结果。

由表12可知，WIC和Nij的预测误差均小于9%。因此，2阶多项式响应面模型具备较高的预测精度，可用于后续研究。

4.4 基于遗传算法的多目标优化

多目标优化是指在满足给定的约束条件下，在设计变量的取值范围之内寻找最优解。大部分情况是不同目标之间存在冲突，几乎无法同时获得最优解，因此多目标优化寻求的是Pareto解集［15］，其数学表达式为

优化变量

优化目标

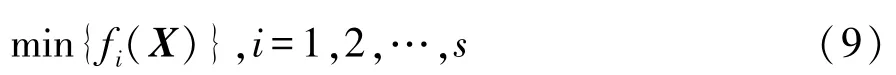
约束条件

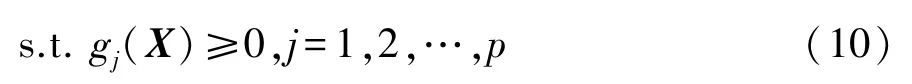
表12 回归方程的取样检验

式中：n为优化变量个数；s为目标函数个数；gj（X）为不等式约束；p为不等式约束个数；hk（X）为等式约束；q为等式约束个数。

非支配遗传算法（non-dominated sorting genetic algorithm，NSGA）具备计算速度快、多方向、全局搜索以及精度高的优势，NGSA-Ⅱ是基于NSGA加上快速优劣排序和新的多样性保持策略，保证群体多样性并降低了计算的复杂度［16］。

结合上述多目标优化原理和遗传算法原理，分析研究综合损伤指标和颈部伤害指标与关键参数关系的优化求解。该多目标优化问题的数学表达式以及约束条件为

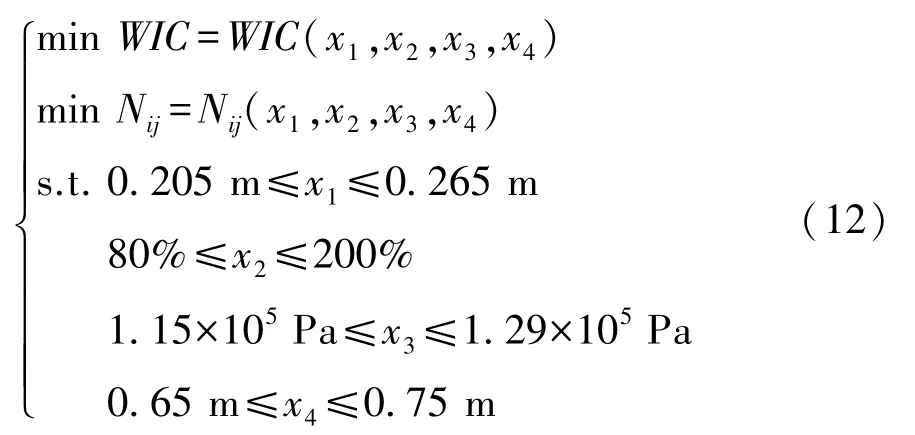
将代理模型和约束参数及其范围输入非支配遗传算法，经过100代遗传算法的迭代获得Pareto前沿曲线图，如图7所示。

由图可见，WIC和Nij不能同时取得最优解。因此针对当前对乘员颈部损伤愈加重视的研究现状，将WIC的权重系数分别设为0.7和0.3，在此条件下，当拉带长度为0.205 m、排气孔开度为200%、排气起始压力为1.15×105Pa以及座间距为0.65 m时，WIC和Nij同时取得较优值，分别为0.184 4和0.238 4。将设计值参数在MADYMO模型中进行设置并仿真分析，仿真值为WIC＝0.2038，Nij＝0.2531。WIC和Nij的仿真值与预测值的误差分别为9.52%和5.8%，误差在可接受范围内。儿童乘员的WIC和Nij分别下降了60.75%和60.94%，大幅提高了儿童乘员的碰撞安全性。

图7 Pareto前沿曲线

5 结论

基于经验证的校车乘员约束模型研究主动式安全气囊控制参数（包括拉带长度、气体质量流率、气囊安装位置、排气孔开度、气囊初始压力、排气起始压力以及座间距）对6岁儿童乘员的保护效果，得出如下结论。

（1）主动式安全气囊与两点式安全带组成的校车儿童乘员约束系统显著降低了6岁儿童乘员在校车正面碰撞中的损伤，提高了6岁儿童乘员的碰撞安全性。

（2）拉带长度、气体质量流率、气囊安装位置、排气孔开度、气囊初始压力、排气起始压力以及座间距等7个参数对6岁儿童乘员的保护均存在一定的影响，通过灵敏度分析方法，分析得出拉带长度、排气孔开度、排气起始压力以及座间距对6岁儿童乘员的WIC和Nij影响较大，其灵敏度值均超过10%。

（3）基于Latin Hypercube试验设计方法设计的仿真和2阶多项式响应面原理，构建了综合损伤指标WIC和颈部损伤指标Nij与拉带长度、排气孔开度、排气起始压力、座间距之间的2阶代理模型。根据该模型，利用多目标优化原理和遗传算法，求得在拉带长度为0.205 m、排气孔开度为200%、排气起始压力为1.15×105Pa以及座间距为0.65 m时，WIC和Nij同时取得较小值。实现在提高儿童乘员综合保护效果的前提下尽可能减少儿童乘员颈部受到的损伤。