薄钢板在CL-20基含铝炸药内爆载荷作用下的变形响应和工程预测
2020-09-28卢广照姜春兰毛亮王在成
卢广照,姜春兰,毛亮,王在成
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
0 引言
钢板作为一种常规的防护构件,在房屋建筑、装甲车辆以及舰船中经常使用,当这些结构遭受恐怖袭击以及军事打击等内部爆炸情况时,内爆炸冲击波的反射和爆轰产物的受限膨胀将使爆炸产生的破坏力比在外部爆炸时要大得多[1-3]。因此,深入研究钢板结构件受炸药内爆炸冲击加载时的变形响应特性是非常必要的。
包括方板、圆板等金属板在爆炸载荷冲击下的响应问题,已被学者们进行了大量理论、试验和数值模拟方面的研究[4-8],涵盖近场爆炸、远场爆炸以及单一加持和全加持等各种条件。Menkes等[9]对冲击加载夹紧梁的情况进行了定义,这些破坏模式被发现也适用于爆炸载荷加载圆板的情况,并经过学者们的研究又进行了更为细致地划分[10-12];孔祥韶等[13]开展了内爆载荷作用下钢板动态响应的仿真研究,建立了封闭空间爆炸载荷的矩形载荷等效方法;姚术健等[14]对多箱室钢结构在内部爆炸载荷作用下的损伤特性进行了研究,根据量纲分析理论,提出了一个适用于内爆响应分析的无量纲数;冯海云等[15]利用全加持的铜薄板进行了自由场中受爆炸载荷变形的实验,建立了一种评估炸药做功能力的新方法,并将其称作金属薄板炸坑法。
针对金属板受到空气自由场中爆炸载荷的变形响应问题以及舰船板架、箱体式结构的变形分析,前人已经进行了较多的研究,而针对全加持的单一薄金属板受内爆炸载荷作用时的变形响应研究还比较少,也较少有考虑含铝炸药爆炸能量输出特性对金属板变形的作用机制。此外,作为迄今为止公认的能量密度和威力最大的单质硝胺炸药,使用六硝基六氮杂异伍兹烷(CL-20)作为基体炸药后能有效提高含铝炸药的能量水平[16-17],但目前有关CL-20基含铝炸药在密闭空间内的爆炸数据也较少见。因此,本文主要针对圆形钢板在受到不同铝含量的CL-20基含铝炸药内爆炸载荷作用下的变形响应规律开展试验研究。
1 试验设计
1.1 试验方法
本试验所采用的爆炸容器罐为椭圆封头结构的钢制压力容器,如图1所示,其中内腔直径为1 200 mm,容积为1.36 m3. 在容器罐主体的中部焊有1根传压管,管长430 mm,利用传压管的滤波作用测量爆炸后期准静态压力信号。传压管顶端设置防爆观察窗,试验时使用高速摄像机记录装药爆炸过程。罐体壁安装压电式传感器测量冲击波压力信号,传压管内壁安装应变式传感器用于测量准静态压力信号。试验前装药使用细棉线吊置于罐体中心与传压管位于同一水平面,如图1(a)中所示,其中S1=340 mm,S2=675 mm. 容器罐装填口以及密封结构示意图如图1(b)所示,圆形密封钢板利用法兰盘和20个等距螺栓进行固定密封,属于夹紧边界条件。密封钢板选用Q235普通碳素结构钢,屈服强度σs=235 MPa,可变形部分的直径2R=460 mm,厚度H=2 mm. 设备连接及实物图如图1(c)和图1(d)所示。
1.2 试验方案
选取铝含量分别为10%、20%、30%的3种CL-20基含铝炸药,铝粉为球状铝粉,粒度中位径为15 μm±5 μm. 此外,还选取了TNT炸药作为对比装药。图2为200 g药量的CL-20基含铝炸药试样,顶部为10 g传爆药柱,试验时使用8号雷管起爆。具体试验工况设计如表1所示,每种工况均进行2次重复性试验。

图2 CL-20基含铝炸药装药试样Fig.2 200 g CL-20-based aluminized explosive charge sample

表1 试验工况Tab.1 Test conditions
2 试验结果与分析
2.1 CL-20基含铝炸药能量释放现象
表2为200 g药量的CL-20基含铝炸药在爆炸容器罐内爆炸后拍摄到的一系列过程图像,从中可以看出,含铝炸药起爆后瞬间发出强烈的爆炸火光,火光持续一段时间后逐渐变暗至熄灭。由于试验药柱的爆轰持续时间在几个微秒内,本试验所用高速摄像机的拍摄间隔为85 μs,捕捉不到这一过程,分析认为表2中火光为爆轰产物的绝热膨胀以及二次燃烧过程。选取发现火光的前一时刻作为0 μs时刻进行分析,可以发现,3种不同铝含量的CL-20基含铝炸药的爆炸火光持续时间均在5.4 ms以内,但随着铝含量由10%增大到30%,火光亮度减弱,火光持续时间由5.355 ms下降至1.7 ms,依次比前者减少了22%和59%,这也意味着爆轰产物的燃烧释能过程随炸药中铝含量的升高而变短。
2.2 CL-20基含铝炸药内爆压力输出特性
图3分别为压力测点b和测点d(见图1(c))采集到的爆炸容器罐内典型的压力- 时间曲线(工况1)。如图3(a)所示,含铝炸药起爆后,初始空气冲击波首先到达传感器壁面,传感器采集反射压力p,经过0.2 ms左右反射压力峰值下降为0 MPa,将这一正压作用区内的冲量定义为初始冲击波的有效冲量;初始冲击波经过多次反射,在密闭空间内不断震荡衰减,变为一段持续上百毫秒的准静态压力波,如图3(b)中黑色曲线所示。结合图3(a)和图3(b)可以看出,在不同时间尺度上,炸药的内爆炸能量分别以初始冲击波和准静态压力波的形式在爆炸容器罐内的空气中传播。

表2 200 g CL-20基含铝炸药爆炸后的高速摄像片段
对准静态压力- 时间曲线利用Origin软件平滑模块中的相邻平均法对压力曲线进行滤波处理,降噪后的曲线如图3(b)中红色线所示(几乎无振荡的曲线),将降噪处理后的压力峰值定义为准静态压力pQS[18]。表3给出了各试验工况下压力曲线的特征值。
根据Cook[19]所提出的含铝炸药爆炸二次反应理论,铝粉在炸药爆轰阶段基本不参与反应,主要在炸药爆轰后的二次燃烧阶段进行反应,因而当试验装药中的铝含量从10%升至30%时,准静态压力逐渐升高,说明铝粉的反应量增加,同时根据表2结果,爆炸罐内的火光持续时间在不断缩短,说明在密闭空间内,提高爆轰产物中的铝粉浓度,能够提高铝粉与爆轰产物的燃烧速率。
此外,密闭空间内炸药爆炸后的准静态压力pQS与装药量m和密闭空间容积V的比值m/V近似呈线性关系[20]:pQS=α(m/V),α为待定系数。文献[20]给出其试验工况下TNT装药对应的比例系数α=3.185. 代入本试验的TNT试验结果进行计算,得到α=3.78,m/V<0.15 kg/m3,也满足线性关系。

图3 爆炸罐内爆典型压力- 时间曲线(工况1)Fig.3 Pressure in explosion vessel (Test 1)
对于CL-20基含铝炸药,图4是每种铝含量下两种装药量的准静态压力变化曲线,由于爆炸容器体积V不变,图4中横坐标以m代替m/V. 由图4可以发现,装药量为200 g时,同一铝含量的准静态压力均小于线性关系下的计算结果(图4中虚线)。随着铝含量由10%升至30%,计算结果较试验值依次偏大14.8%、15.5%和25%. 分析认为:这是由于含铝炸药中的铝粉燃烧时会消耗大量空气中的氧,同时铝颗粒燃烧机理复杂,因而装药量翻倍后,容器内的铝粉浓度翻倍,密闭容器内的空气量不变,导致铝粉的反应度因装药量升高而降低,准静态压力未呈线性关系。
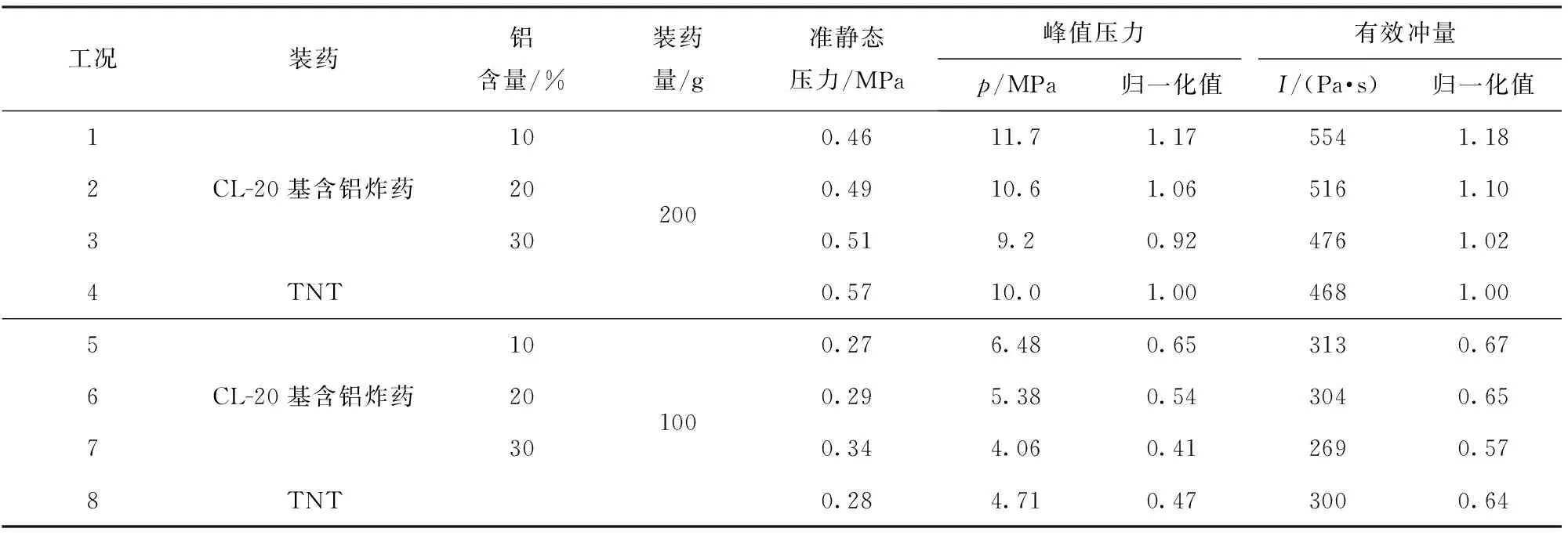
表3 试验压力数据Tab.3 Test results of overpressure and quasi-static pressure
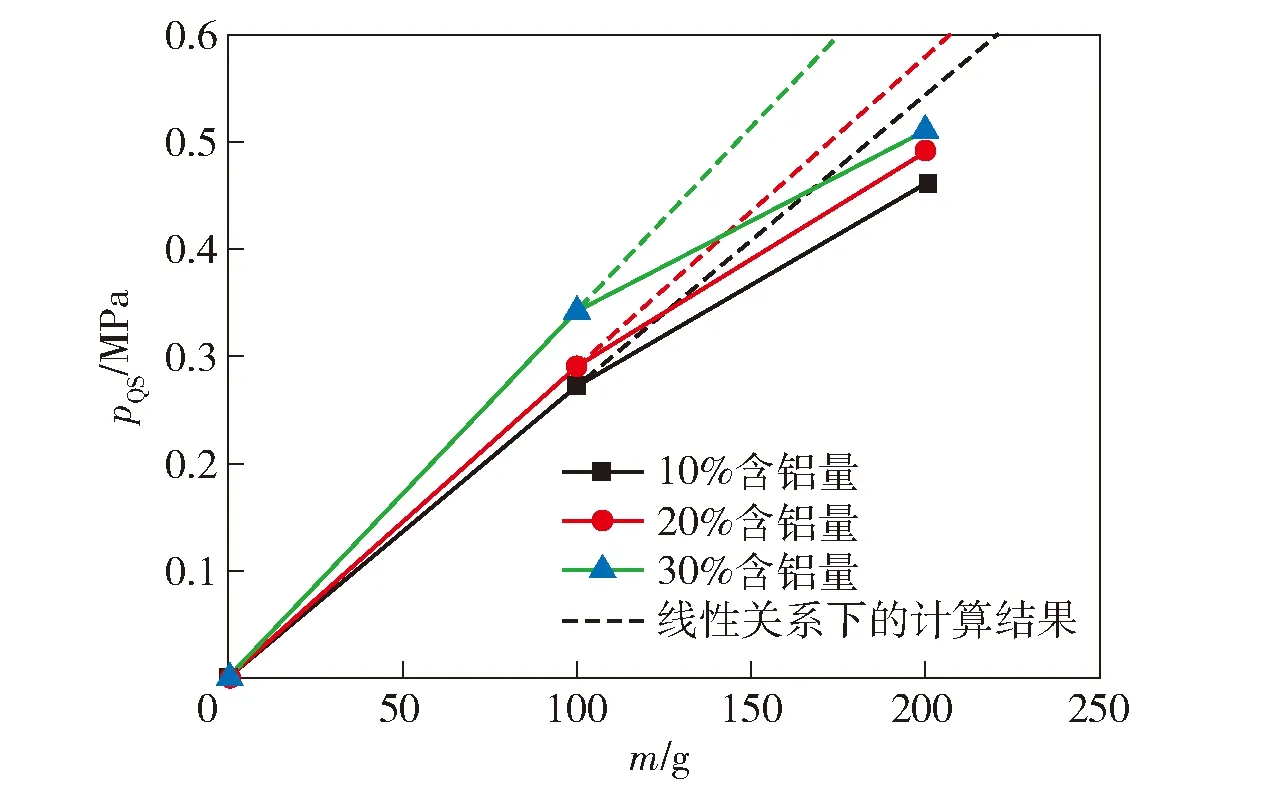
图4 爆炸容器内CL-20基含铝炸药的准静态压力值Fig.4 Quasi-static pressure values of CL-20-based aluminized explosives in explosion vessel
Dong等[21]研究发现球形容器壳体的初始响应取决于内爆炸冲量和初始冲击波的形状。因此,对于初始冲击波的峰值压力和有效冲量,二者作为表征爆炸初始冲击波能的重要参量,以200 gTNT装药的压力数据(工况4)为基准,分别对两种装药量的峰值压力和有效冲量进行归一化处理,以便将二者的变化趋势进行同时对比,见表3.
由于CL-20含量在相应减少,导致冲击波压力峰值不断降低。图5给出了归一化后的初始冲击波压力峰值和有效冲量随铝含量的变化趋势,铝含量升高后二者分别减小的比例也在图中标出。从图5中可以看出,二者随铝含量的升高具有相同的变化趋势,但从下降比例上可以看出,有效冲量相比于冲击波压力峰值降低得更加缓慢。这是由于含铝炸药爆轰结束后,爆轰产物进行厌氧膨胀,推动初始冲击波进行传播,此阶段铝粉已开始与其他爆轰产物进行燃烧反应[22],分析认为,虽然含铝量的升高,降低了炸药爆轰阶段释放的初始能量(正如测到的峰值压力和有效冲量的变化所示),但此时铝粉与爆轰产物进行了燃烧释能,因此能够部分抵消有效冲量的降低趋势,这也与裴明敬等[23]的发现相一致。初始冲击波的有效冲量衰减得相对缓慢,说明有效冲量相比于超压峰值,能够更充分地体现含铝炸药爆炸的初始冲击波能。

图5 归一化后的冲击波压力峰值和有效冲量随铝 含量的变化曲线Fig.5 Normalized pressure peak value and effective impulse of initial shock wave versus aluminum content
2.3 密封钢板的变形结果分析
图6和图7分别是200 g和100 g装药量的CL-20基含铝炸药爆炸冲击密封钢板后钢板的变形失效结果。根据试验后密封钢板变形区域的变形状态划分钢板的失效模式。从图6和图7中可以看出,密封钢板出现未破裂的塑性大变形并且最大残余变形点基本位于钢板中心。从图6中可以看出,200 g装药量时,钢板的约束边界均出现局部颈缩变形,且随着铝含量由10%升至30%,颈缩变形逐渐减小。根据文献[10-12]划分的金属板失效模式可以确定,200 g含铝炸药爆炸冲击后的钢板变形失效模式均为MODE Ⅰa型,具体为塑性大变形且局部边界发生颈缩变形。由图7可知,100 g装药量的内爆炸载荷并未造成钢板局部边界出现颈缩变形,失效模式为MODE Ⅰ型,单纯的塑性大变形。

图6 200 g CL-20基含铝炸药爆炸冲击下的密封 钢板边界变形情况Fig.6 Damage modes of sealing steel plates under internal blast loading of 200 g CL-20-based aluminized explosives
根据试验后密封钢板的残余变形量评估其变形程度。图8为钢板变形挠度的测量方式示意图,沿经过最大变形量的直径,使用深度尺每隔5 cm进行一次测量。对每种配方2发试验的测量结果求平均值,由此确定了钢板径向切面的变形轮廓和最大残余变形量。表4给出了每种工况中钢板的变形轮廓数据。
表4中数据以距离为横坐标x轴,以钢板的变形挠度为纵坐标y轴,绘制成挠度曲线图,如图9所示。由图9可以看出,对于100 g和200 g装药量产生的内爆炸载荷,钢板存在明显的变形响应差异,图中虚线即为分界线。对于同一种装药量,不同铝含量下CL-20基含铝炸药的内爆炸释能差异也能够造成钢板不同程度的变形响应。密封钢板的变形响应对于200 g装药量中铝含量的变化更加敏感。

图7 100 g CL-20基含铝炸药爆炸冲击下的密封钢板 边界变形情况Fig.7 Damage modes of sealing steel plates under internal blast loading of 100 g CL-20 based aluminized explosives

表4 密封钢板变形轮廓数据(挠度)Tab.4 Deformation data (deflection) of steel plate cm

图8 试验后的密封钢板残余变形挠度测量示意图Fig.8 Schematic diagram of residual deflection measurement of test sealing steel plate

图9 不同装药类型下密封钢板切面的变形轮廓Fig.9 Deformation profiles of steel plate sections
综合上述结果,这些变形响应差异说明了CL-20基含铝炸药中铝粉在二次燃烧阶段释放的能量能够对冲击压垮钢板起到一定作用。随着铝含量由10%升至30%,对于两种装药量,钢板的最大残余变形逐渐减小,钢板约束边界的颈缩变形程度也逐渐变小。由表3可以发现,这两个结果均与内爆炸初始冲击波有效冲量随铝含量的变化趋势相一致,而与罐内准静态压力的变化趋势相反,说明密封钢板的变形失效程度主要与炸药内爆炸初始冲击波能有关,这里的初始冲击波能由有效冲量来表征。
为研究密封钢板最大残余变形量和初始冲击波有效冲量之间的关系,以钢板在200 g TNT内爆炸冲击下的最大残余变形量为基准进行归一化处理(转化为TNT当量),见表5和图10.
由表5可以发现,对于密封钢板的最大残余变形量,以200 g TNT的试验结果为基准,200 g CL-20基含铝炸药的爆炸冲击结果最大为TNT的1.17倍(工况1)。随着含铝量的升高比值降低,最低为TNT的1.03倍(工况3)。
从表5和图10可以看出:最大残余变形量和有效冲量的TNT当量非常接近;且装药量越大越接近,小药量时偏差较大,与钢板的强度有关;即证明了密封钢板的最大残余变形量是由炸药内爆炸初始冲击波的有效冲量决定的。

表5 密封钢板最大残余变形量与有效冲量归一化值Tab.5 Normalized values of maximum residual deformation and effective impulse
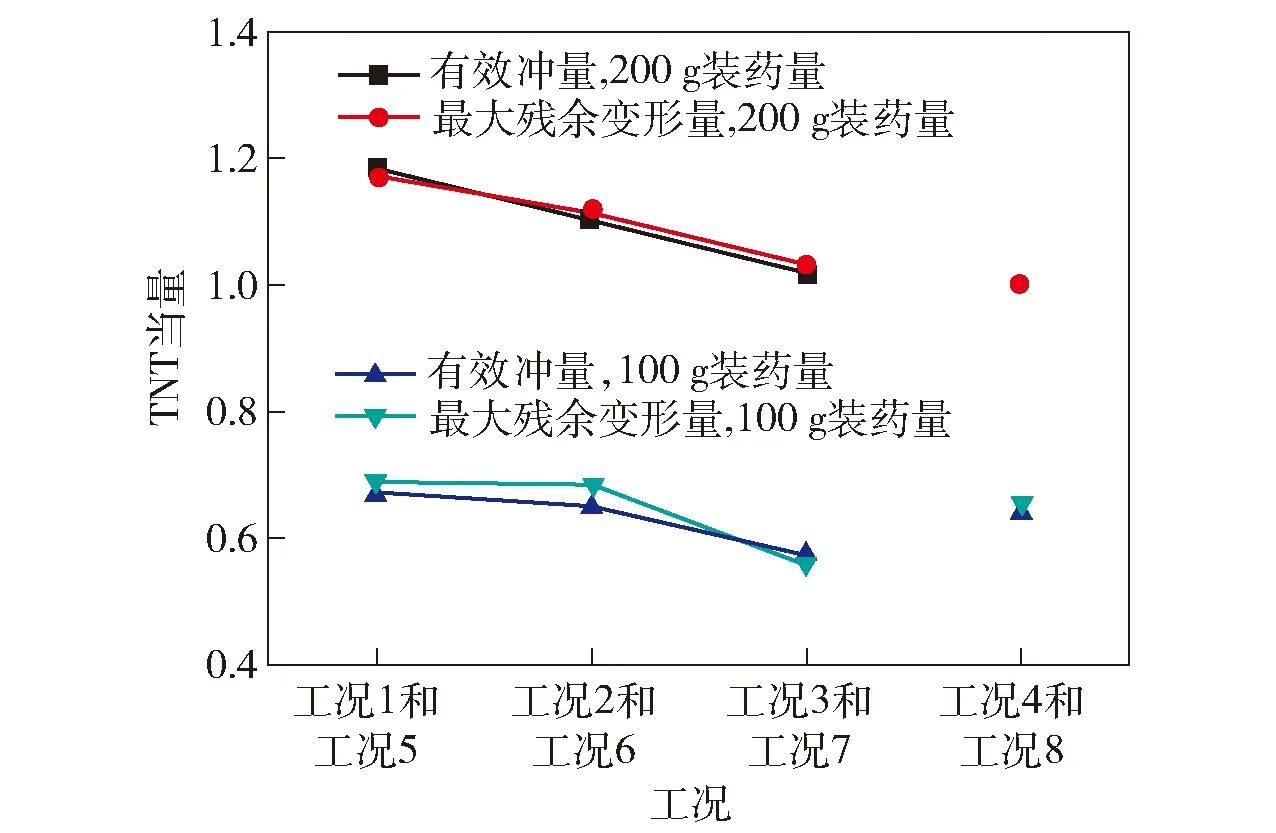
图10 内爆炸初始冲击波有效冲量和钢板最大残余变形量计算的TNT当量对比结果Fig.10 TNT equivalents calculated from the effective impulse of initial shock wave and the maximum residual deflection of steel plate
图11给出了不同装药量下密封钢板的最大残余变形量,从中可以发现,当装药质量翻倍后,不论是含铝炸药还是TNT,钢板中心残余变形量均未达到2倍变化,说明密封钢板的变形响应与试验装药量呈非线性相关。

图11 不同装药量下密封钢板最大残余变形量Fig.11 Comparison of the maximum residual deflections of sealing steel plates under the conditions of different charge masses
3 密封钢板最大残余变形挠度预测
装药在爆炸容器罐中爆炸后初始冲击波在罐内的传播情况如图12所示。为预测内爆载荷作用下钢板的变形情况,建立最大残余变形量和初始冲击波有效冲量(即炸药爆炸初始冲击波能)之间的关系,作如下假设:
1)忽略装药结构带来的影响;
2)忽略容器罐侧壁反射波对向爆炸容器罐顶端钢板传播的初始冲击波影响;
3)初始冲击波到达顶端颈部时近似为理想球面波,进入颈部管路后近似为平面波传播,冲击波对钢板以均布载荷的形式作用。
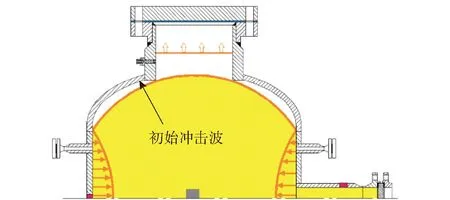
图12 爆炸冲击波在爆炸容器罐内的传播示意图Fig.12 Propagation of the initial shock wave in pressure vessel
密封钢板的最大塑性变形程度可用(1)式[24]计算得到:
(1)
式中:δ为钢板的最大残余变形量;λ为Jones[24]提出的一个无量纲参数,用来预测在受到速度均布的冲击载荷时全夹持板的非弹性变形度,
(2)
μ为钢板单位面积的质量,μ=ρH,ρ为钢板密度,v0为冲击波撞击钢板前的速度,M0=σsH2/4.
无量纲数λ亦可化为
(3)
式中:I为冲击波对钢板的冲量。从(3)式可以发现,Jones数λ中,起决定性作用的炸药能量输出参数是冲击波对钢板的冲量I,这也与图10得到的结论相一致。
Remennikov等[4]提出了一种爆炸冲击波冲量分析模型,以球形装药的瞬态爆轰模型为基础,距离装药中心r处目标表面单元所受的冲量i的大小为
(4)
式中:w为稀疏波在爆轰产物中的传播速度;up为爆轰产物由装药表面向外扩散的粒子运动速度,up=D/(1+k),D为炸药爆速,k为等熵指数;Rc为装药半径;ρc为装药密度;r为装药到目标表面单元的直线距离;s为装药到目标表面的垂直距离。
(5)
由(5)式对钢板面积进行积分可求得钢板所受的冲击波总冲量I为
(6)
考虑到爆炸容器罐颈部的存在,对爆炸能量具有约束聚焦作用[4],会使得钢板所受冲量比理论计算值要大,引入约束系数α对模型进行修正,其值可由试验数据确定,于是(6)式变为
(7)
因此,新的无量纲数λα为
(8)
于是,计算最大塑性变形程度的(1)式,就变为(9)式:
(9)
以TNT对薄钢板的作用为基准,将装药量m=200 g以及最大挠度δmax=6.22 cm依次代入(6)式、(9)式和(8)式中,可分别求得I=50.36 Pa·s,λα=5 960,Iα=151.53 Pa·s.
于是,可由(7)式获得约束系数α=3. 约束系数的大小可能与装药位置和颈部长度及内径有关。
表6给出了各种试验工况下密封钢板的最大残余变形量计算结果。图13是密封钢板最大残余变形量的试验值和分析模型计算值的对比结果。由图13和表6可以看出,计算结果与试验结果十分接近,二者的最大偏差为5.1%. 说明修正后的该工程预测模型能够对不同类型装药爆炸加载下密封钢板的变形情况进行有效预测。

图13 最大残余变形量的试验值与工程模型计算结果对比Fig.13 Comparison between the experimental and calculated values of maximum residual deflection
图14中给出了钢板最大残余变形和钢板厚度的比值与修正后的Jones数λα的关系,拟合获得的曲线方程为
(10)
4 结论
本文利用爆炸容器罐试验测试系统,研究了圆形钢板在不同铝含量的CL-20基含铝炸药内爆炸载荷作用下的变形响应特性。得到主要结论如下:
1)压力测试结果表明:相比于初始冲击波的峰值压力,有效冲量能更全面地体现炸药爆炸初期释放的能量;密闭容器内的准静态压力和爆轰产物的燃烧速率随铝含量的升高而升高,且前者与装药量呈非线性关系。
2)相比于准静态压力的作用,密封钢板的最大残余变形量主要取决于炸药内爆炸初始冲击波的有效冲量。10%铝含量的CL-20基含铝炸药能产生更高的初始冲击波有效冲量,导致钢板的变形和失效程度更大。随着铝含量升高至30%,钢板的变形失效程度逐渐变小。考虑到罐体结构的特殊性,本结论仅适用于本文相似试验工况下的现象。

表6 钢板最大残余变形量计算结果Tab.6 Calculation of the maximum residual deflection of sealing steel plates
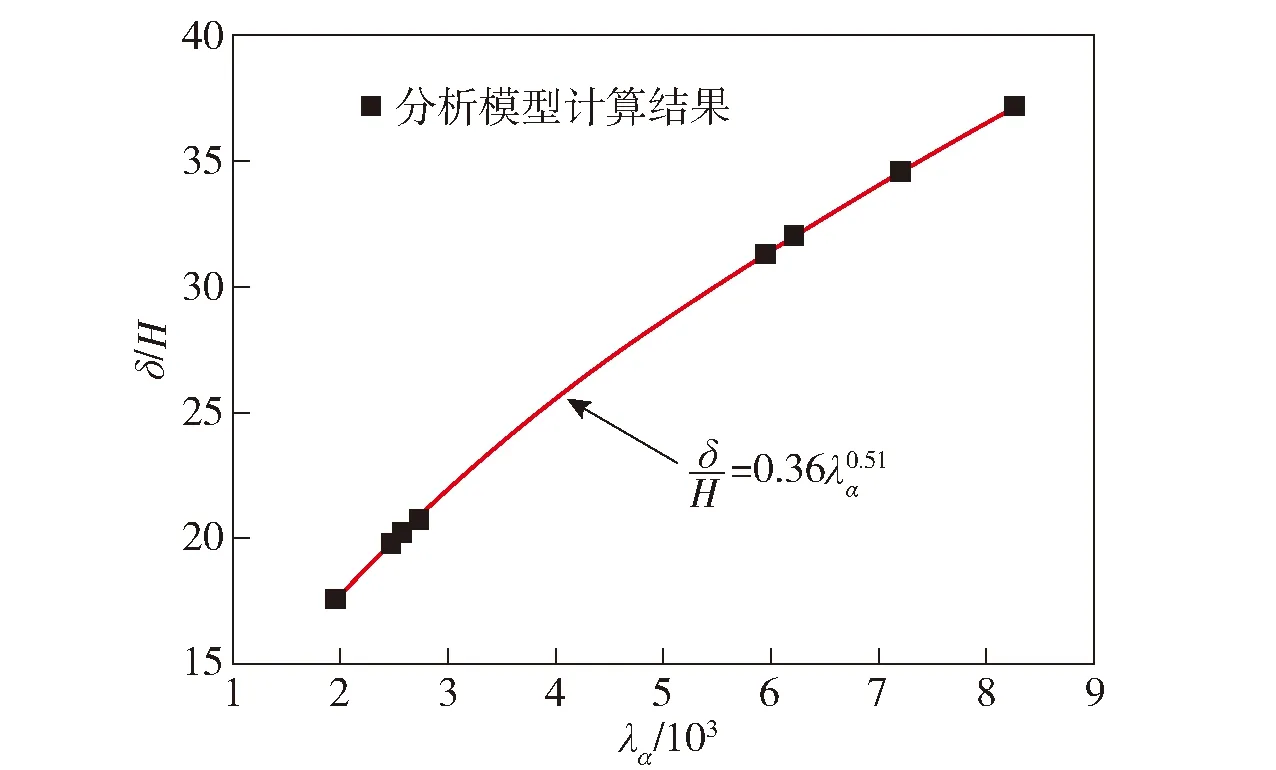
图14 钢板中心变形量与厚度的比值和修正后的Jones数的拟合曲线Fig.14 Midpoint deflection-thickness ratio versus modified Jones dimensionless number λα
3)本文所建立的钢板在内爆载荷作用下最大残余变形的工程计算方法能够有效预测不同类型装药爆炸加载下密封钢板的变形情况。但文中拟合得到的具体公式,仅适用于本文相似试验工况下的金属板变形预测。
