二进制偏置载波信号伪码周期联合估计方法

张笑宇，冯永新，钱博

(沈阳理工大学 辽宁省信息网络与信息对抗重点实验室，辽宁 沈阳 110159)

0 引言

直扩信号淹没在噪声中传播，具有较强的抗干扰性和抗截获性，广泛应用于各种通信系统中[1]。随着直扩通信技术的发展，具有更好的抗干扰和抗多径能力的二进制偏置载波(BOC)信号得到广泛关注和研究[2]。考虑到BOC信号频谱分裂的优势，对BOC信号进行精确的伪码周期估计，对现代通信对抗有至关重要的意义。

作为一种新型调制信号，BOC信号的研究主要集中在捕获与跟踪，针对该信号的参数估计问题研究很少。文献[3]通过谱相关方法实现了BOC信号的相关参数估计，但其伪码速率的信噪比估计容限仅为-11.5 dB. 文献[4]使用二次谱法完成了多径信道下时分数据调制(TDDM)-BOC信号的伪码周期估计，但随着信噪比的逐渐降低，累加次数逐渐增大，估计算法的收敛性较差。

正交分路法[5]是一种通过正交分路相关处理以去除BOC信号中载波和噪声对自相关函数(ACF)影响的信号处理方法。相对于传统的二次谱法[6]，正交分路法将正交分路与二次谱相联合，可以有效去除信号中噪声和载波对ACF的影响，得到更精准的信号相关函数特征，提高参数估计的精度。

因此本文将正交分路法引入传统二次谱中进行BOC信号伪码周期估计，提出一种BOC信号伪码周期估计的新方法，以实现低信噪比未知信号参数条件下的伪码周期估计。

1 BOC信号及其特性分析

BOC信号的数学表达式[7-8]如下:

S(t)=A·D(t)P(t)Sc(t)cos (2πft+φ)，

(1)

式中：S(t)为BOC调制信号；A为信号的幅度；D(t)为信息码，D(t)=±1；P(t)为扩频码速率fc的扩频码,P(t)=±1；Sc(t)为亚载波速率fs的亚载波,Sc(t)=±1；f为载波频率；φ为初始相位。BOC信号调制由信息码模、扩频码模块和亚载波模块实现，其调制原理如图1所示[9-10]。

BOC信号的调制阶数n是由载波频率f和亚载波速率fs共同决定的，且满足n=2fs/f. 根据调制阶数的不同，BOC信号可分为奇数阶BOC信号和偶数阶BOC信号[11]。

图1 BOC信号调制原理图[9-10]Fig.1 Modulation principle of BOC[9-10]

图2 BOC信号的PSDFig.2 PSD of BOC modulation signals

BOC信号优秀的裂谱特性是在直扩调制的基础上引入亚载波，采用相同扩频码序列的BOC(2，2)、BOC(6，1)、BOC(8，4)3种典型信号的功率谱密度(PSD)和ACF，如图2和图3所示。

图3 BOC信号的ACFFig.3 ACF of BOC modulation signals

由图2可知：3种BOC信号的PSD均呈现频谱裂开的特性，且BOC(8，4)、BOC(6，1)、BOC(2，2)的PSD主瓣与副瓣之和分别为4、12、2，主瓣宽度分别为8 MHz、6 MHz、2 MHz左右，副瓣宽度分别为4 MHz、1 MHz、2 MHz左右。能量集中的主瓣幅值分别在74 dBW/Hz、84 dBW/Hz、82 dBW/Hz左右，副瓣能量分别集中在67 dBW/Hz、76 dBW/Hz、65 dBW/Hz左右，主瓣大于副瓣一个能量级左右。因此，BOC信号的裂谱特性使其可以与其他直扩信号在主瓣能量不重叠的基础上同频传输，从而提高通信信道的利用率；且与常规直扩信号带宽相比，BOC信号的带宽更宽具有更强的抗干扰能力。

BOC信号的ACF表达式[12-13]为

(2)

式中：τ为码间延时；N为常数；T为伪码周期；l为以τ=0开始的峰值两侧编号，l=0，±1，…，±n-1.

由图3可见，3种BOC信号的ACF均呈现多个峰值的特性，自相关峰值随着延迟的递增而递减。BOC信号中的相关峰数目m=2n-1由扩频码速率fc与亚载波速率fs的比值决定，且归一化自相关峰中峰值高度为(-1)l(n-|l|)/n，各峰值之间的间隔均为1/2fs.

2 二次谱法机理

二次谱法将信号的功率谱作为输入信号，再次求功率谱。根据调制阶数的不同，BOC信号功率谱同样可分为奇数阶BOC信号功率谱和偶数阶BOC信号功率谱[14]。

1)调制阶数n为奇数，

(3)

式中：GBOC(f)为BOC信号的功率谱。

2)调制阶数n为偶数，

(4)

由于ACF和功率谱互为傅里叶变换对，在求出输入信号ACF的基础上进行傅里叶变换，进而得到信号的功率谱。BOC信号二次谱[15]可表示为

(5)

式中：Gs(e)为二次谱密度函数；Ns为采样点数。由(5)式可知，经过二次谱处理后，BOC信号的能量聚集在一些较尖锐的三角形脉冲序列处，脉冲间距为伪码周期的整数倍；而高斯白噪声的功率谱经过二次谱处理后不具备此特性。因此，通过相邻三角形脉冲序列的峰值，便可有效估计BOC信号的伪码周期。

在常规BOC信号处理中，传统二次谱法可以有效地进行参数估计，但在复杂战场电磁环境下，信噪比环境较差，噪声将会影响载波分量中脉冲序列的峰值大小，从而引发误判，错误估计BOC信号的伪码周期。因此本文引入正交分路相关法，将二次谱法和正交分路相联合，完成低信噪比条件下BOC信号伪码周期的有效估计。

3 正交分路法机理

正交分路法通过正交分路相关处理，去除BOC信号中载波和噪声对ACF的影响，得到更精准的BOC信号相关函数特征，可在未知参数条件下有效提高BOC信号的参数估计精度[16-17]。基于正交分路的基本原理框图如图4所示[18-19]。图4中，fl和φl为本地载波的载波频率和初始相位，y(τ)为正交分路处理结果。

图4 正交分路去载波原理框图[18-19]Fig.4 Principle of removing carrier based on orthogonal two-way[18-19]

经过高斯白噪声信道后的BOC信号[20-21]可表示为

S(t)=
A·D(t)P(t)Sc(t)cos(2πft+φ)+n(t)，

(6)

式中：n(t)为高斯白噪声，其均值为0.

对BOC信号进行正交混频处理，带噪BOC信号分别乘以cos (2πflt+φl)和sin (2πflt+φl)后，同相支路I和正交支路Q的表达式为

(7)

分别对同相支路和正交支路信号进行低通滤波，则可将(7)式改写为

(8)

对滤波后的I支路和Q支路信号分别求ACF，以I支路信号为例，其ACF可表示为

RII(τ)=RS′IS′I(τ)+RS′InI(τ)+RnInI(τ) ，

(9)

式中：RS′IS′I(τ)为信号ACF；RS′InI(τ)为信号和噪声的互相关函数；RnInI(τ)为噪声ACF.

由于BOC信号和噪声互不相关，满足RS′InI(τ)→0，则同相支路ACF可简化为

RII(τ)=RS′IS′I(τ)+RnInI(τ) ，

(10)

式中：RnInI(τ)≈N0δ(τ)，N0为高斯白噪声功率谱密度，δ(τ)为冲击响应函数。

BOC信号部分的ACF可表示为

(11)

(11)式代入(10)式后，(10)式改写为

(12)

同理，正交支路信号的ACF和两支路的互相关函数分别如下：

(13)

(14)

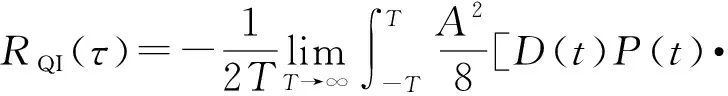
(15)

式中：

(16)

为消除积分项对ACF的影响，对同相支路和正交支路的ACF求和，以及对同相支路和正交支路的互相关函数求差的表达式为

(17)

式中：

(18)

(16)式、(18)式代入(17)式，(17)式可化简为

(19)

对上述两个结果求平方和后，可最终得到正交分路的结果如下：

(20)

由(20)式可见，通过正交分路的BOC信号开平方操作即可得到BOC信号基带序列的ACF，此时ACF中已经消除载波成分，并降低了噪声对信号的影响[22]。在此基础上，对去除载波和降低噪声的ACF进行二次谱分析，可以在低信噪比下有效完成BOC信号的参数估计。

4 新方法估计流程及性能分析

对I路或Q路带残留载波的BOC信号直接二次谱分析同样可以估计伪码周期，但带残留载波的估计效果与传统二次谱的效果相似，在较低信噪比条件下，残留载波分量仍将影响脉冲序列的峰值大小，从而引发误判，仍无法精确地对BOC信号进行伪码周期的估计；正交分路的二次谱方法对残留载波进行抵消操作，可得到更准确的BOC信号相关函数特征，有效提高BOC信号的伪码周期估计精度。

因此，本文在传统谱估计理论基础上，提出联合正交分路和二次谱后的BOC信号伪码周期新方法，其原理框图如图5所示，估计流程如下：

步骤1将接收BOC信号分别与两支路的本振信号相乘，进行低通滤波，得到I、Q支路信号。

步骤2 分别计算两支路信号的ACF和互相关函数，将两支路的自相关结果相加，将两支路的互相关结果相减。

步骤3 对求和结果与求差结果进行求平方和处理，得去载波后的正交分路结果。

步骤4 将正交分路结果进行开平方处理后再取绝对值，并进行归一化处理。

步骤5 求归一化结果的傅里叶变换，得到信号的功率谱。

步骤6 对功率谱再次进行傅里叶变换，然后对其模值进行求平方处理，得到信号的二次功率谱；对离散谱线进行峰值搜索，根据峰值最大位置及采样频率估计出伪随机码周期。

图5 基于正交分路的二次谱伪码周期估计原理框图Fig.5 Schematic diagram of PN sequence period estimation based on orthogonal two-way

联合正交分路和二次谱后的BOC信号伪码周期的计算复杂度，由正交分路部分复杂度和二次谱部分的复杂度组成。正交分路的计算复杂度为O(M2)+O(M)；二次谱的复杂度为O(MlgM)，即联合方法的计算复杂度为O(M2)+O(M)+O(MlgM)。但由于正交分路中的ACF和互相关函数可以利用快速傅里叶变换快速完成，复杂度将降低为O(MlgM)+O(M)，联合方法计算复杂度也将降低为O(MlgM)+O(M)。

5 仿真与分析

为了验证本文所提新方法的可行性和正确性，以BOC(10，5)为例，用MATLAB软件对BOC信号伪码周期估计性能进行验证与分析。具体仿真参数如下：载波频率为40.92 MHz，伪码速率为10.23 MHz，亚载波速率为5.115 MHz，采样频率为163.68 MHz，伪随机序列长度为1 023，信道为高斯白噪声信道。

图6所示为-10 dB信噪比下正交分路去载波和未去载波的ACF结果对比图。由图6可见：未消除载波的自相关结果在局部自相关峰值范围内包含多个峰值，在未知信号参数的条件下参数估计性能必将受到影响；正交分路去载波后的自相关结果中，由于对正交和同相支路的互相关结果采用相减方式处理，消除了载频成分的影响，有利于更低信噪比条件下BOC信号精确的参数估计。

图6 信噪比为-10 dB下的正交分路处理结果(局部放大)Fig.6 Processing results of orthogonal two-way at -10 dB SNR (partial enlarged detail)

为了验证联合估计方法与传统二次谱方法的伪码周期估计性能，图7和图8分别给出了联合估计方法和传统二次谱法在-10 dB和-19 dB信噪比下二次谱归一化峰值的实验结果。经过大量仿真实验，两种方法的阈值设定为0.7.

图7 传统二次谱归一化峰值结果Fig.7 Estimated results of raditional secondary spectrum method

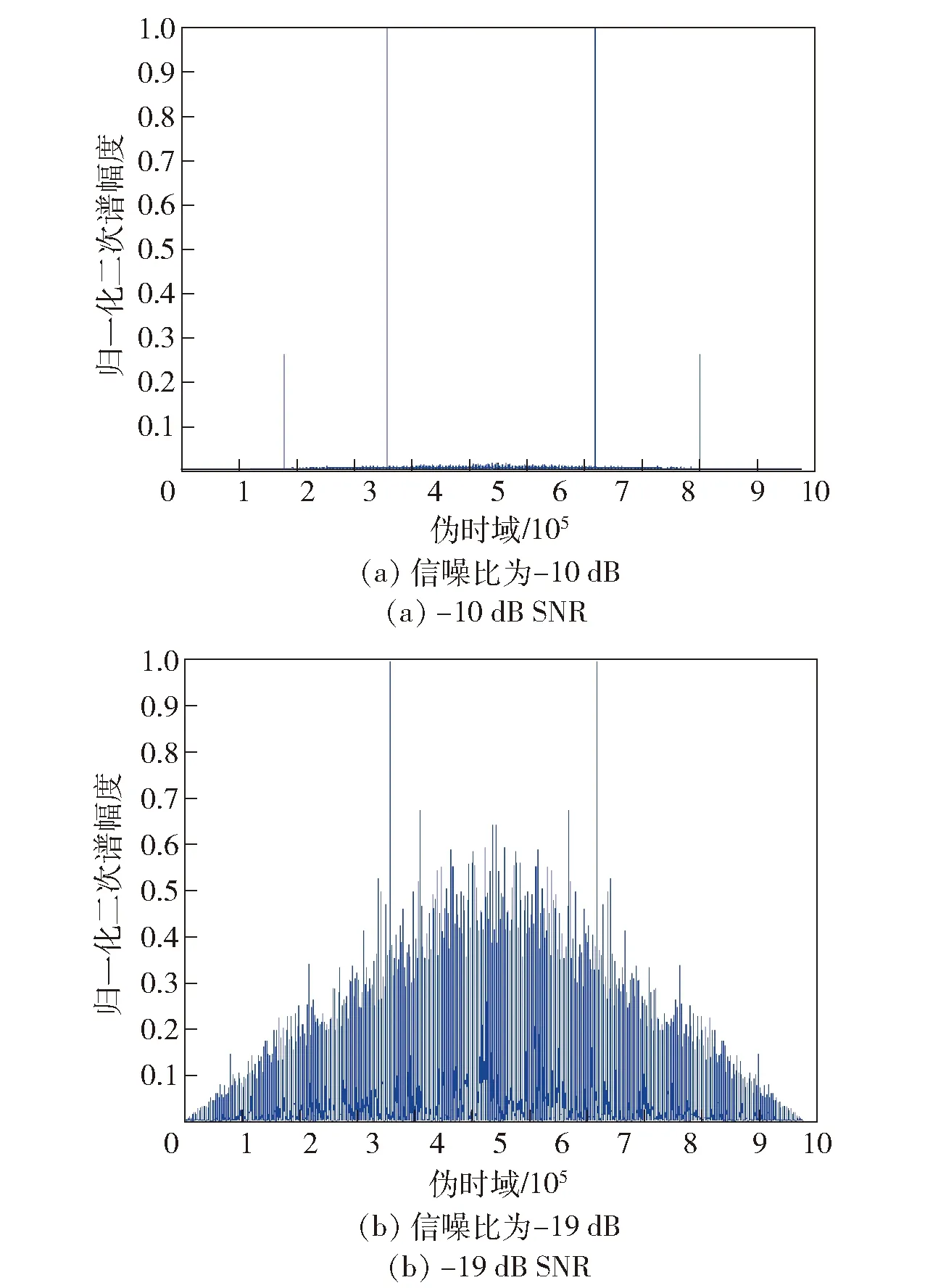
图8 联合估计方法二次谱归一化峰值结果Fig.8 Estimated results of the proposed estimation method

由图7可见，在-10 dB和-19 dB信噪比下，传统二次谱法均存在离散的峰值。当信噪比为-10 dB时，根据阈值计算的峰值最大值估计的伪码周期均为16 368个采样点，由于产生的BOC信号伪码周期长度1 023个码片，且通过采样频率可知1个码片对应16个采样点，因此BOC信号伪码周期对应的采样点数应为16 368，传统二次谱方法在-10 dB下可有效估计BOC信号的伪码周期；当信噪比为-19 dB时，传统二次谱法由于载波分量的存在，受载波和噪声影响较大，超过阈值的峰值较多，此时传统二次谱法已无法正确估计BOC信号的伪码周期。

由图8可见，在-10 dB和-19 dB信噪比下，联合估计方法均存在离散的峰值。当信噪比为-10 dB时，根据阈值计算的峰值最大值估计的伪码周期均为16 368个采样点，由于产生的BOC信号伪码周期长度1 023个码片，且通过采样频率可知1个码片对应16个采样点，因此BOC信号的伪码周期对应的采样点数应为16 368，联合估计方法在-10 dB下可有效估计BOC信号的伪码周期；当信噪比为-19 dB时，联合估计方法在载波去除后仍具有较为明显的离散谱线，且根据阈值计算的峰值最大值位置伪码周期采样点数仍为16 368，联合估计方法在-19 dB下仍然可有效估计BOC信号的伪码周期。由此可以验证，联合估计方法相比传统二次谱法可在更低信噪比条件下有效估计BOC信号的伪码周期。

图9所示为联合估计方法与传统二次谱方法的信噪比容限随码长变化曲线。由图9可知，相对于传统二次谱法，联合估计方法在载波去除后，在码长为8 191时可提高3 dB的信噪比容限，且随着伪随机码码长的不断增大，联合估计方法性能更优。

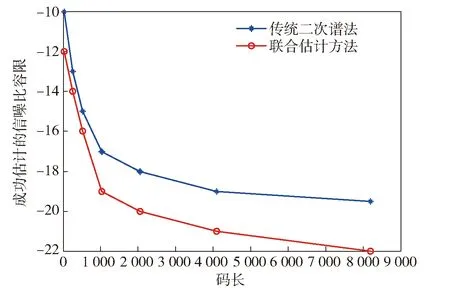
图9 两种二次谱法估计性能对比曲线Fig.9 Estimation performances of two methods

图10所示为联合估计方法与传统二次谱方法在信噪比为-20～0 dB条件下伪码周期估计误差变化曲线(仿真次数为500次)。由图10可知，相对于传统二次谱法，联合估计方法由于去除载波分量的影响估计误差更小，精度更高，尤其是在信噪比较低条件下。

图10 两种二次谱方法估计误差对比曲线Fig.10 Comparison of estimated errors of two methods

为了验证不同类型BOC信号的伪码周期估计性能，图11给出了不同调制系数下BOC(2，2)、BOC(6，1)、BOC(8，4)在-20～0 dB条件下伪码周期估计误差变化曲线。由图11可以看出，不同调制系数下的伪码周期估计性能相当，表明联合估计方法与调制系数无关，可以适用于不同类型的BOC调制信号。

图11 不同类型BOC信号估计性能对比曲线Fig.11 Estimated errors of BOC signals with different modulation coefficients

6 结论

本文在分析BOC信号自相关特性基础上，针对二次谱法信噪比容限低的不足，提出一种BOC信号伪码周期联合估计方法。通过引入正交分路去除噪声和载波的影响，得到基带调制序列的ACF，并采用二次谱法对离散谱线进行统计分析，实现BOC信号的伪码周期估计。为验证伪码周期的估计性能，通过设置合理参数，在不同信噪比条件下进行仿真对比分析。仿真结果验证了联合估计方法可提高BOC信号伪码周期估计的信噪比容限3 dB.