基于卷积神经网络的路面识别及半主动悬架控制

2020-09-28刘秋孙晋伟张华胡煦顾亮

兵工学报 2020年8期

刘秋，孙晋伟，张华, 胡煦，顾亮

(1.北京理工大学振动与噪声控制研究所，北京 100081；2.西安航空学院车辆工程学院，陕西西安 710077；3.内蒙古一机集团宏远电器股份有限公司，内蒙古包头 014000)

0 引言

车辆行驶过程中，实时准确地获取当前的路面类型，可为车辆操纵稳定性、舒适性的改善提供重要信息。因此，能否准确识别车辆当前行驶的路面十分关键。

针对路面识别，目前主要采用以下两种方法进行识别：1)通过加速度传感器、位移传感器采集由不同路面激励引起的系统响应，通过对系统响应信号进行分析和处理，对不同的路面进行分类识别；2)利用车载摄像头采集路面图像，通过对图像处理提取路面的纹理特征，从而对不同路面进行分类。

目前国内外研究人员对路面识别方法进行了大量研究，并取得了一定成果。Ward等[1]通过放置于悬架摆臂上的加速度传感器，对砖石路、草路和沙石路等非城市路面进行了分类，将测量的加速度信号传递至动态车辆模型来估计地形轮廓，最后利用监督学习支持向量机(SVM)实现路面类型的识别。Qin等[2]通过布置于车身上的加速度传感器测量簧载质量加速度来提取路面的时频特征，对不同幅值或频率的路面激励引起簧载质量加速度变化特征进行识别，从而对不同国家标准路面等级(B级～F级)进行识别。Ngwangwa等[3]首先利用汽车振动系统8自由度模型，基于非线性自回归(NARX)神经网络并通过仿真建立了车辆响应和路面不平度的关系，其次通过传感器测试和处理得到相应的车辆响应，最后应用预训练完成的NARX神经网络识别路面不平度。Bekhti等[4]首先通过摄像机采集前方的路面图像，其次通过相应计算估计路面的纹理特征，最后计算路面纹理特征和振动情况的相关性，从而对前方路面的振动情况进行预测。Decatur[5]利用人工神经网络提取雷达地形图像的纹理特征对图像进行分类，并与传统的使用最大似然估计的贝叶斯分类进行对比，证明了前者的识别效率与精确度优于后者。王世峰等[6]使用加速度传感器和图像特征数据融合对非城市路面进行识别，并使用反向传播(BP)神经网络进行了分类。

尽管上述方法均能较准确地识别路面，但也存在一定缺陷。例如，当路面粗糙程度较差时(非城市路面)，采用加速度传感器和位移传感器很难保证识别的精度；而采用图像识别时没有考虑自然环境下强光照、弱光照、图像倾斜、图像局部缺失等特殊情况对图像质量的影响。此外，利用传统BP神经网络对图像进行分类时需对图像进行较复杂的人为预处理，无法直接将原始图像数据作为网络的输入，同时当网络神经元较多时BP神经网络的权重参数会十分巨大，使网络分类效率大大降低甚至无法进行分类。

本文通过采集路面图像数据并利用卷积神经网络(CNN)对路面类型进行识别。CNN的优势在于它能够通过简单的卷积与池化运算从原始输入图像中自行提取特征，并根据BP算法自动更新网络参数从而对图像进行学习。为了模拟自然环境以及车辆振动对摄像头采集图像质量的影响，对训练数据集进行数据增强，即随机抽取若干路面图像、人为调整其明暗度，或对图像进行一定角度的翻转、剪切以及一定像素的平移，以提高CNN识别的泛化能力。最后采用遗传优化算法寻找不同路面下半主动悬架系统最优参数，并根据路面识别结果实现悬架控制参数在不同路面下的自适应调整。

1 1/4半主动悬架模型

本文以1/4车辆模型为基本框架，利用磁流变(MR)减振器模型作为阻尼元件、刚度为定值的传统螺旋弹簧模型作为弹性元件组成1/4半主动悬架模型。

1.1 磁流变减振器模型

磁流变减振器外特性通常具有强烈非线性并带有迟滞环，其建模的精确与否对悬架控制有较大影响。非参数化模型、伪静力模型和参数化动力学模型是目前常用的3种磁流变减振器模型。其中参数化动力学模型对MR减振器外特性描述得最全面和准确。因此本文根据Kwok等[7]提出的参数化动力学模型对其进行建模。MR减振器迟滞模型示意图如图1所示。

图1 MR减振器迟滞模型Fig.1 MR damper hysteresis model

模型由迟滞部分、弹性部分、阻尼部分三者并联组成，考虑上述三者的动力学特性，最终可得到MR减振器数学模型如下：

(1)

(2)

Kwok等[7]通过对MR减振器进行外特性试验以及参数识别，得到上述待定参数的数学表达式，其中：

c=1 929I+1 232，

(3)

k=-1 700I+5 100，

(4)

α=-244I2+918I+32，

(5)

β=100，

(6)

δ=0.3I+0.58，

(7)

f0=-18I-257，

(8)

式中：I为MR减振器控制电流(A)，I⊂[0 A,2 A]。

对模型加载幅值为0.08 m，频率为2 Hz的正弦激励。控制电流为0～2 A，间隔为0.25 A，则MR减振器速度特性曲线以及示功图分别如图2、图3所示。

图2 MR减振器速度特性曲线Fig.2 Speed characteristic curves of MR damper

图3 MR减振器示功图Fig.3 Indicator diagram of MR damper

1.2 1/4车辆模型

1/4车辆模型如图4所示。图4中，mb和mw分别表示簧载、非簧载质量，Ks、Kt分别表示悬架刚度和车轮刚度，xb、xw和xr分别表示簧载质量位移、非簧载质量位移和路面激励。

图4 1/4车辆模型Fig.4 Quarter vehicle model

建立1/4车辆非线性系统模型如下：

(9)

(10)

1.3 路面不平度采集

将路面相对基准平面的垂直方向高度记为q，沿道路纵向的长度记为L，q随着L变化的函数称为路面不平度函数，记作q(L)。目前路面不平度的测量技术主要有不动基准测量法、随动基准测量法、动态响应测量法、角度基准测量法等[8]。本文采用角度基准测量法，分别对沥青路、水泥路、砂石路、弹石路路面不平度进行测量。测量仪器以及路面图像分别如图5、图6所示。

图5 路面不平度测试仪器及车辆Fig.5 Road roughness test equipment and vehicle

图6 路面图像Fig.6 Road images

图7 水泥路路面不平度实测曲线Fig.7 Measured curves of cement road surface roughness

4种路面不平度曲线如图7～图10所示。国家标准A级～F级路面按照1984年国际标准化组织文件ISO/TC 108/SC2N67中提出的表达式进行拟合[9]：

(11)

式中：Gq(n)表示路面不平度功率谱密度，n为空间频率(m-1)；n0为参考空间频率，n0=0.1 m-1；Gq(n0)为n0下的路面功率谱密度值，称为路面不平度系数(m3)；W为频率指数，分级路面谱的频率指数W=2. 各等级路面不平度系数Gq(n0)的几何平均值如表1所示。

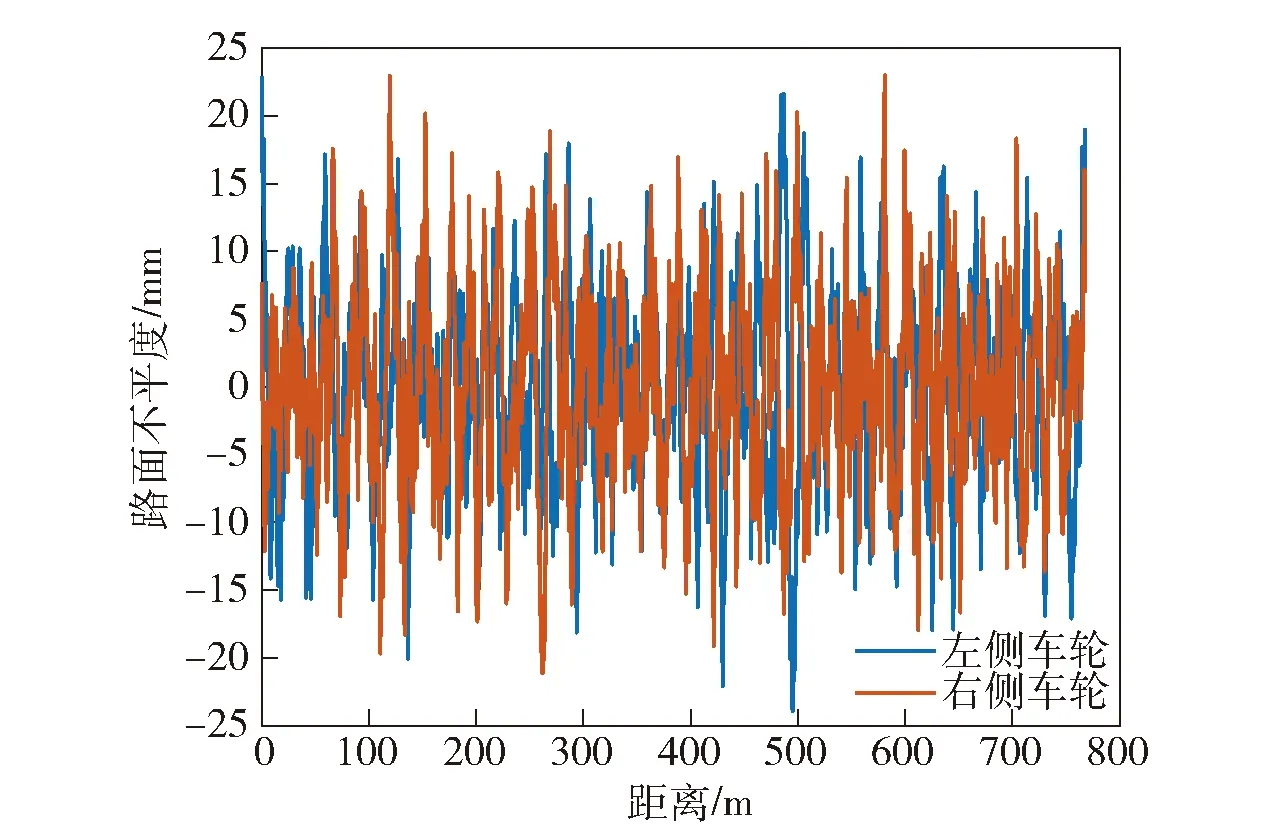
图8 沥青路路面不平度实测曲线Fig.8 Measured curves of asphalt road surface roughness

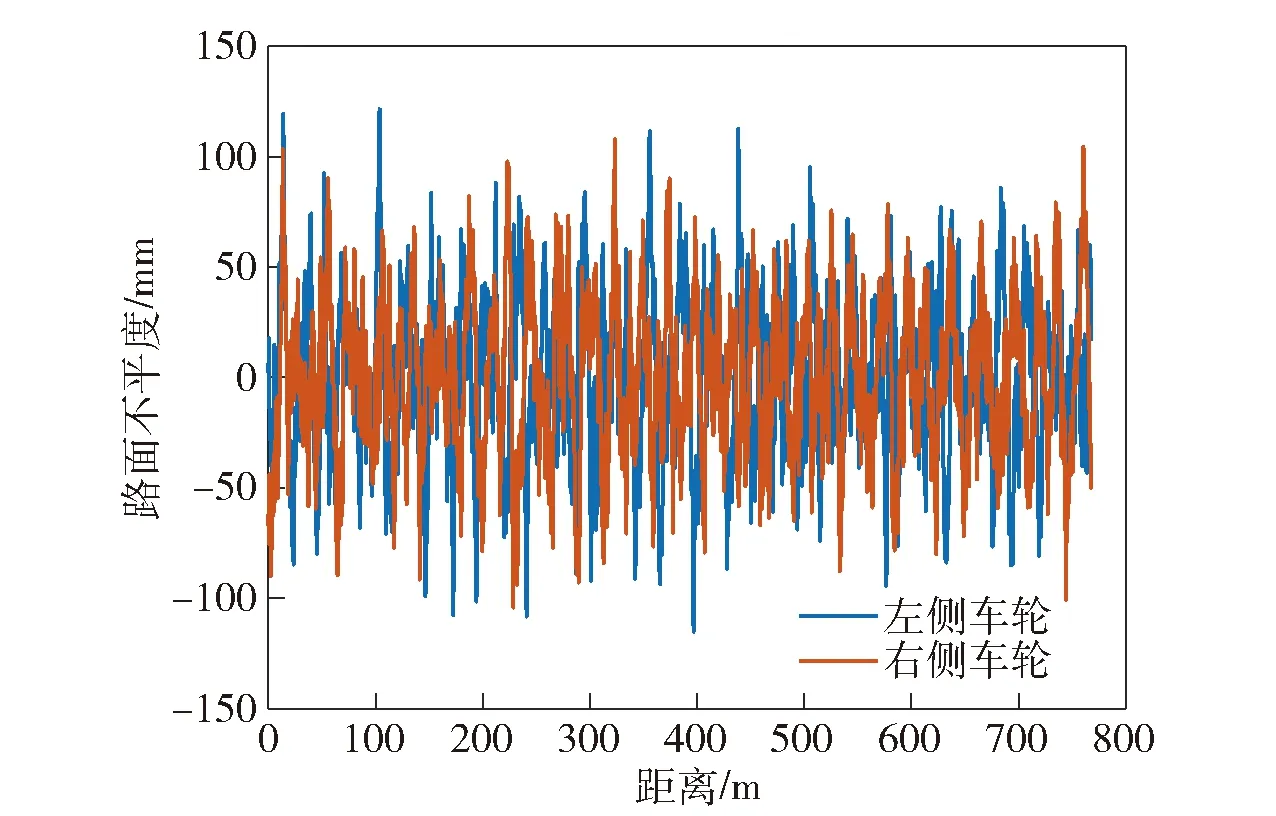
图9 弹石路路面不平度实测曲线Fig.9 Measured curves of pebble road surface roughness

图10 砂石路路面不平度实测曲线Fig.10 Measured curves of sandstone road surface roughness

表1 A级～F级路面不平度系数几何平均值Tab.1 Roughness coefficient geometric means ofA-F grade roads

将采集的4种路面与国家标准路面对比，如图11所示(双对数坐标系)。由图11可见，在路面垂直位移功率谱密度曲线高频段(空间频率在0.28 m-1以上)，沥青路基本与C级路面重合，水泥路介于C级、D级之间，砂石路、弹石路分别与D级、E级路面基本重合。

图12 CNN结构图Fig.12 Convolutional neural network structure

图11 4种路面与国家标准等级路面功率谱密度曲线Fig.11 Power spectral density curves of four road surfaces and national standard grade road

2 基于卷积神经网络的路面图像识别

传统的图像识别方法通常不能将原始图像直接作为分类器的输入进行识别，需要利用不同算法人为地提取图像纹理、颜色、或者一些更高级的特征，然后将计算得到的特征作为分类器的输入进行分类识别。

深度学习动机在于建立、模拟人脑进行分析学习的神经网络，模仿人脑的机制来解释数据，例如图像、声音和文本。CNN作为深度学习框架之一，在图像识别领域取得了巨大成功，相比传统的图像识别方法，其优势在于它能够通过简单的卷积与池化运算从原始输入图像中自行提取特征，并根据BP算法自动更新网络参数从而对图像进行学习，是一种端到端的学习。同时CNN中神经元的稀疏连接以及参数共享能够极大降低模型的计算量，使得更深的网络结构、更高像素的图像输入成为可能。

2.1 CNN结构

本文通过搭建相应的CNN对不同的路面图像数据进行学习，最终实现对路面识别的目的。所搭建的CNN结构如图12所示。图12中，包括13个卷积层、5个池化层、3个全连接层以及最后的Softmax输出层。

针对图像数据，卷积层中卷积的运算[10]如下：

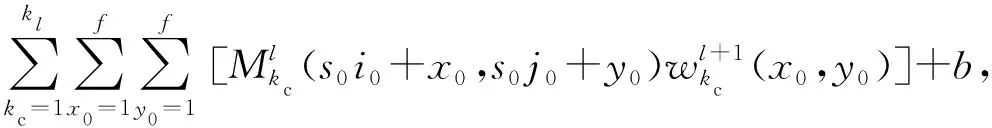
(12)

在卷积层进行特征提取后，输出的特征图传递至池化层进行特征选择，将特征图中单个点的像素值替换为其相邻区域像素值的统计量，以达到降维的目的。池化层进行特征选择的方式主要有平均池化和最大池化。本文采用最大池化，即选取相邻区域内像素值的极大值[11]。

当卷积核为大小f=1、步长s0=1的单位卷积核且不包含填充时，则(12)式表示全连接层内的矩阵乘法运算：

(13)

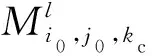
Softmax函数能将一个含任意实数的N维向量p压缩到另一个N维实向量σ(p)中，使得每一个元素的取值范围都在(0,1)之间，并且所有元素之和为1. 即将图12中全连接层3的输出转化为输入图像属于每一类别的概率[10]：

参照国内《兽用消毒剂鉴定技术规范》[8]及《消毒技术规范》[9]试验方法进行。将菌株分别接种到琼脂培养基划线培养,传至3 代,挑取单个菌落接种到相应的肉汤培养基中,37 ℃培养18～24 h,再分别接种到斜面培养基放4 ℃冰箱,储存备用。

(14)

式中：pi为N维向量p中的第i个元素。

在加快网络训练速度的同时，为了防止梯度爆炸或消失以及陷入较差的局部最优值，本文通过批量归一化规范各层网络激活函数的输入，防止训练陷入激活函数中饱和的非线性区域，从而加快网络的收敛速度[12]。对于训练中某一个批量的数据{x1,x2，…，xP}，该数据可以是输入也可以是网络中间某一层的输出，数据批量归一化操作如下：

(15)

(16)

(17)

式中：μ为数据均值；xj为数据个数P中第j个数据；σ2为数据方差；l为数据归一化值；γ和θ为两个需要网络学习的参数；ε为人为给定的参数；l为归一化后的最终输出。

2.2 数据增强

针对CNN，良好的泛化能力比较高的训练准确率更为重要。良好的泛化能力意味着CNN对训练数据以外的数据同样具有准确预测的能力[13]。提高CNN泛化能力的一个有效措施就是对训练数据集进行数据增强，即人为创建假数据并添加至训练集[14]。本文首先收集4种典型的城市以及非城市路面图像，其次对部分路面图像进行图像处理，即调整图像明暗度、将图像沿横向或垂向平移若干像素、对图像进行小角度的翻转和剪切，从而模拟外部自然环境以及采样时车辆振动对图像质量的影响，达到数据增强的目的。原始图像以及进行图像处理的图像如图13所示，图像处理参数如表2所示。

3 仿真分析

3.1 半主动悬架控制流程

路面识别以及半主动悬架控制流程(见图14)由路面图像采集、路面类型识别、半主动悬架控制三部分组成。由图14可见：首先，通过摄像头采集路面图像作为CNN的输入；其次，通过预训练完成的CNN对输入图像进行识别；最后，根据识别结果选择已经过遗传算法优化的半主动悬架控制参数，实现悬架控制参数在不同路面下自适应调整以提升车辆性能的目的。本文以4种路面进行仿真分析，对于普遍情况可通过增加数据集中路面类型的种类来拓宽CNN识别范围。同时加载不同的路面激励信号并结合优化算法获取不同路面类型下悬架的最优控制参数。

图14 基于路面识别的半主动悬架控制流程图Fig.14 Flow chart of semi-active suspension control based on road recognition

3.2 卷积神经网络训练以及验证

本文收集了1.3节中所述4种路面类型的图像数据，即城市沥青路、水泥路、砂石路以及弹石路。每种路面类型经过数据增强后分别有10 000个样本，一共40 000个样本。其中30 000个样本组成训练集用于CNN训练，10 000个样本组成验证集用于验证CNN训练效果。训练集与验证集中每种路面图像占样本总个数的比例相同。同时每个样本均通过MATLAB软件处理为228×228×3的红、绿、蓝彩色图像作为CNN的输入，并采用监督学习的方式对卷积神经网络进行训练。

CNN网络训练中的卷积、池化、误差BP更新权重等操作需要进行大量的矩阵运算，为了加快网络的训练速度，本文调用图形处理器进行网络训练。用于网络训练的设备如表3所示，网络参数设置如表4所示。

表3 网络训练所用硬件Tab.3 Hardware for network training

表4 卷积神经网络参数Tab.4 Convolutional neural network parameters

CNN训练以及验证的准确率、损失函数值曲线如图15所示。由图15可知，训练过程仅在200次迭代后就基本收敛，此时训练集与验证集的准确率曲线、损失函数值曲线走势基本重合，数值上准确率接近于1，损失函数值接近0. 训练完成后，通过编写程序从包含10 000个样本的验证集中随机选取18个样本导入已训练完成的卷积神经网络中，18个样本的识别结果如图16所示。图16中，每个子图样本下方给出了CNN识别的结果及其对应的概率。由图16可知，训练完成的CNN对本文采集的4种典型城市及非城市路面具有较好的识别以及泛化能力。同时通过添加计时程序可计算出：在所使用的硬件设备下(见表3)，单张路面图像的识别用时约为9.5 ms.

图15 卷积神经网络训练及验证结果Fig.15 Training and verified results of convolutional neural network

3.3 4种路面仿真结果

为保证车辆在不同类型的路面行驶时均具有良好的舒适性以及操纵稳定性，需对MR减振器针对不同的路面类型提供不同控制电流，以得到合适的阻尼特性。根据所建立的1/4车辆半主动悬架模型，以MR减振器控制电流为优化变量，以悬架动行程为约束条件，以簧载质量加速度、车轮动变形的均方根值为优化目标[15]，针对不同的路面激励求取MR减振器的最优控制电流。本文以某车型被动悬架参数作为参照，通过对优化目标赋予权重系数的方式，将多目标优化问题转化为单目标优化问题，然后结合遗传算法进行求解。所确定的目标函数如下：

(18)

图16 随机样本测试结果Fig.16 Test results of random samples

遗传算法参数设置如下：

1)使用精英操作，每代选择20个优秀个体直接遗传，不参与交叉与变异；

2)种群大小为200；

3)遗传代数为50代；

4)交叉与变异概率分别设置为0.3、0.1；

5)控制电流搜寻范围[0 A,2 A]；

6)悬架最大动行程设置为12 cm.

路面激励信号采用所采集的4种路面不平度时域信号。从车辆动力学的角度来看，车辆的舒适性与操纵稳定性是一对相互矛盾的指标[16]，因此应根据具体路面来为目标函数分配不同的加权系数。当路面较差时，应着重优化与车辆操纵稳定性相关的指标。当路面良好时，应着重优化与车辆舒适性相关的指标。用于参照的被动悬架参数如表5所示，不同路面类型下目标函数加权系数取值以及优化后的控制电流如表6所示。

乘坐舒适性与操纵稳定性优化结果如图17、表7所示。通过半主动悬架与被动悬架的对比可知：对于路面良好的沥青路、水泥路而言，簧载质量加速

表5 被动悬架参数表Tab.5 Passive suspension parameters

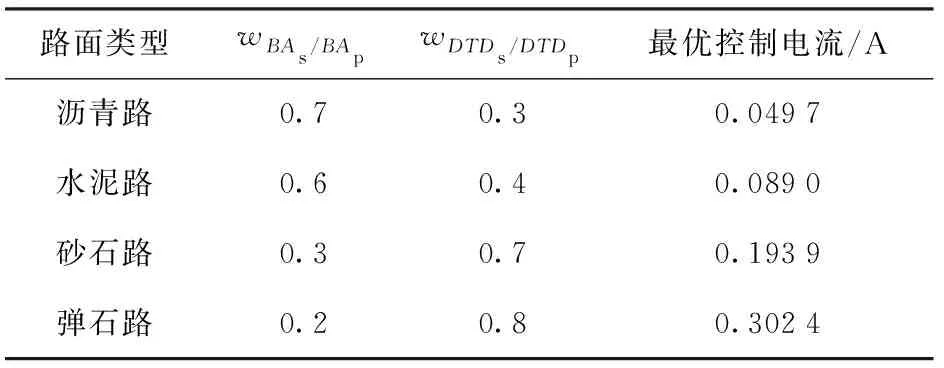
表6 4种路面加权系数及最优控制电流Tab.6 Weighting coefficients and optimal control current of four roads

度均方根值、车轮动变形均方根值均得到了有效改善；而对于路面较差的砂石路、弹石路，在有效降低车轮动变形的同时簧载质量加速度仅有小幅度的恶化。

4 结论

本文首先建立基于MR减振器的车辆1/4半主动悬架模型，其次通过搭建CNN基本结构并利用所采集的4种典型城市以及非城市路面图像对网络进行训练和测试，并通过训练完成的卷积神经网络对路面类型进行识别。采用遗传优化算法并以所采集的4种路面不平度时域信号作为路面激励求取半主动悬架最优控制参数，根据路面识别结果及优化结果实现悬架控制参数的自适应调整。得出主要结论如下：

1)加入数据批量归一化和数据增强操作，在提高网络收敛速度的同时使得网络具有良好的泛化能力。

2)基于卷积神经网络的路面识别方法能对所采集的4种城市以及非城市道路进行准确识别。

3)基于路面识别和遗传算法的半主动悬架控制系统，可根据不同路面类型自适应调整MR减振器控制电流，提升车辆在良好路面下舒适性的同时改善了在较差路面下的操纵稳定性。

在目前所做工作的基础上，后续工作重点将放在增加路面图像数据集样本数量与种类，进一步扩展CNN的识别范围，以及通过代码硬件部署开展实车控制的相关研究工作。