基于模糊控制策略的快速反射镜伺服控制

高歆杨，柯芳，邹伟，余潇，袁佳

(西南技术物理研究所, 四川 成都 610041)

0 引言

快速控制反射镜(FSM)简称快反镜，是一种可以快速、精确地调整光束方向的伺服控制装置。快反镜具有响应速度快、控制带宽高、抗干扰能力强等优良特性，被广泛地应用于天文望远镜、激光通信、图像稳定光学系统、自适应光学系统、光电跟踪瞄准系统等领域[1-5]。快反镜通常与大转角的跟踪架一起构成复合轴系统，由跟踪架主系统完成大范围的粗跟踪，快反镜子系统保证跟踪精度的实现。作为跟瞄回路中的关键环节，快反镜需要具备更快的响应速度和更高的精度才能满足系统日益增长的需求，而优良的伺服性能是实现高精度快速跟踪的前提条件，因此设计出可靠且易于工程实现的控制算法来提升快反镜伺服性能，从而保证复合轴系统达到需求的跟踪精度具有迫切的现实意义[6-9]。

文献[10]采用改进根轨迹设计PID参量，保证了系统动态性能同时还改善了快速反射镜结构的机械谐振问题，但是需要知晓系统模型精确的数学表达式，所以泛用性不高；文献[11]采用自适应算法，弥补了传统PID不能根据实际情况在线整定控制器参数的不足，提高了跟踪精度与稳定性，但是其计算原理复杂，很大程度上依赖Lyapunov函数的选取；文献[12]采用改进自抗扰的方法，在原有自抗扰算法的基础上减小了响应时间，提升了跟踪精度，但是其只验证了低频信号下的跟踪精度，缺乏实现工程化的理论保障。

模糊控制作为智能控制的一个分支，是控制理论及控制工程目前研究的一个重要方向。模糊控制器通过综合利用领域专家的控制经验来应对实际工况的变化，可以在不依赖被控对象精确的模型参数情况下自适应整定控制参数，因此相比传统PID控制器，既能显著改善控制品质，又具有较好的鲁棒性。模糊控制方法不仅得到仿真实验验证，而且已经成功应用于多种对象的实际控制系统中[13]，如文献[14]将模糊控制算法应用于汽车悬架系统，解决了系统非线性以及不确定性等问题，很好地抑制了随机输入信号下的误差干扰。因此，本文针对复合轴跟踪的应用背景，提出将模糊控制算法应用于快反镜伺服控制系统，提高快反镜的抑制带宽，达到更加有效抑制主轴残差的目的。

本文拟从系统设计层面探索高性能快反镜的控制方法，提出一种将模糊控制策略与PID结构相结合的模糊控制器，既继承PID便于工程实现的优点，又可克服控制参数无法自适应整定的不足，赋予PID方法一定的智能性，从而更好地适应不同的运行工况，达到全面提升现有快反镜控制性能的目的。以基于高频摇摆电机的快反镜为应用对象设计了模糊控制器，对实际工况下快反镜的伺服性能进行了仿真研究，通过与传统控制下伺服性能的对比，验证了本文提出的模糊控制器可以显著改善快反镜伺服性能，为进一步提升复合轴跟踪精度建立了基础。

1 用于复合轴跟踪的快反镜控制结构

一种用于复合轴跟踪的快反镜控制结构是由光电跟踪外环与位置伺服内环(快反镜伺服装置)组成的双环控制结构，外环与内环的控制框图分别如图1和图2所示，图1中的虚线表示通过目标空间的光路闭环。本文目的是解决伺服内环的性能提升问题，为后续的外环控制系统研究奠定基础。表征快反镜伺服性能的主要指标有：抑制带宽、阶跃响应的超调及上升时间、随机输入响应能力等。

图1 快反镜光电跟踪外环控制框图Fig.1 Block diagram of outer loop control of FSM electro-optic tracking

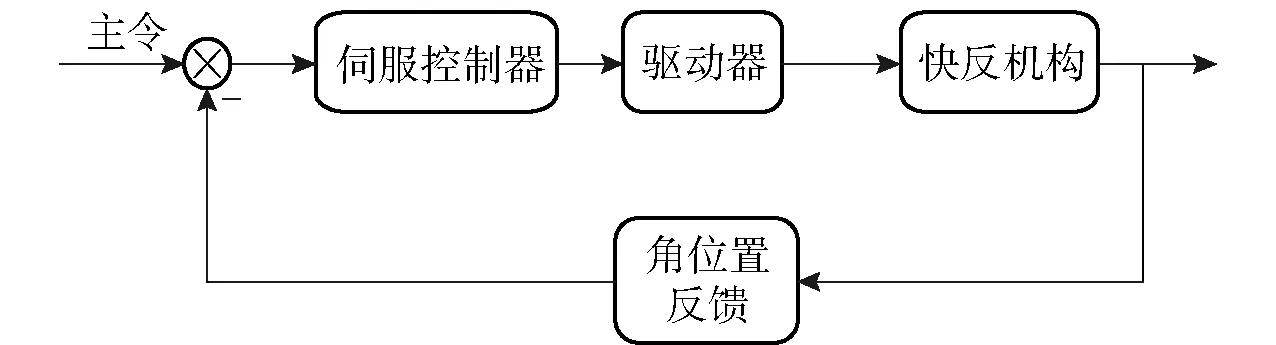
图2 位置伺服内环(快反镜伺服装置)控制框图Fig.2 Control block diagram of position servo inner loop (FSM servo device )

目前，传统PID控制由于技术成熟、实现简单可靠，而成为快反镜控制系统最普遍的控制方式[15]。但是，随着对控制品质要求的提高，PID控制的缺点便显现出来：一般只适用于线性系统、需知晓被控对象的模型参数才能获得较为理想的PID参数，若控制系统结构特性随时间变化则难取得较好控制效果[16]，而且传统PID其控制参数由人为事先计算确定，因而对于实际工况下输入信号特性的随机变化难于自适应[17]、基于PID控制的回路抑制带宽有限等。

2 模糊思维及其控制原理

模糊思维是针对所有思维对象进行的非精确思维，而模糊控制便是基于这种思维并以模糊集合论、模糊语言变量以及模糊逻辑推理3个部分为基础构成的计算机控制[18]。整个模糊控制系统主要分为两个部分，模糊控制器和被控对象。其中，模糊控制器为该系统的核心，由以下4个部分组成[19-21]：

2.1 模糊化

将输入的精确量转换成模糊化量。具体过程为：将精确的输入量进行尺度变换到各自的论域范围，再对其进行模糊处理转化成模糊量。一般采用线性变换。

例如，实际输入量xi的实际变化范围为[amin,amax]，而xi的模糊论域为[bmin,bmax]，则如(1)式所示。

(1)

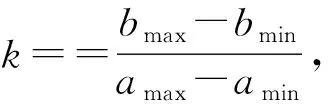
2.2 知识库

知识库通常由提供处理模糊数据相关定义的数据库以及由逻辑语言来描述控制目标和策略的规则库两部分组成。知识库包含被控对象应用领域中的相关知识，是领域专家控制经验的综合反映，也是从实际控制经验过渡到模糊控制器的关键环节。

2.3 模糊推理

模糊推理是整个模糊控制器的核心，它可以模仿人类做决定时的模糊概念，运用模糊逻辑进行推理，从而得到模糊控制量。该推理工作原理是基于模糊逻辑中的函数关系及相对应的推理规则来进行的。通常具有如下形式：

IF…(一组条件)…THEN…(得出结论)…。

2.4 去模糊化

去模糊化的作用是将由模糊推理环节得到的模糊控制量经过适当的函数关系变换为实际用于控制被控对象的清晰控制量。主要的去模糊方法有3种：1)最大隶属度法；2)面积平均法；3)重心法。重心法取μC′(z)加权平均值为z的清晰值，如(2)式和图3所示。

(2)

式中：μC′(z)为隶属度函数，C′为模糊集合，z为输出量；zo为输出量清晰值，它类似于重心的计算。

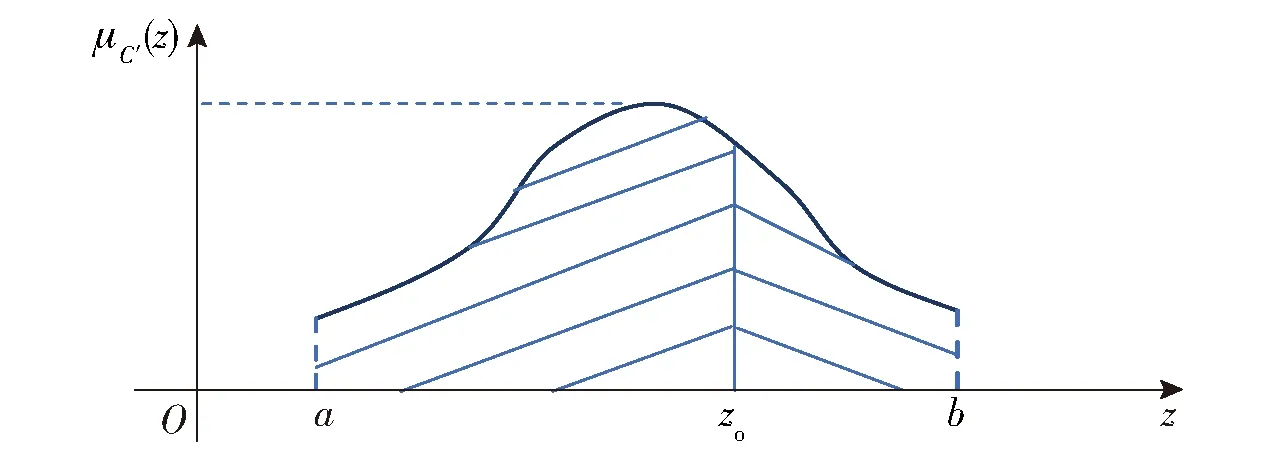
图3 清晰化重心法Fig.3 Centroid method

3 快反镜模糊控制器设计原理与步骤

3.1 概述

本文提出将模糊策略与传统PID概念相结合设计一种适用于快反镜伺服系统的模糊控制器，该模糊控制器依旧采用传统PID的结构，但比例、积分、微分3个控制参数依据输入偏差及偏差变化率实时调节，而调节规则来自领域专家的控制经验，由模糊推理生产。具体设计步骤如下。

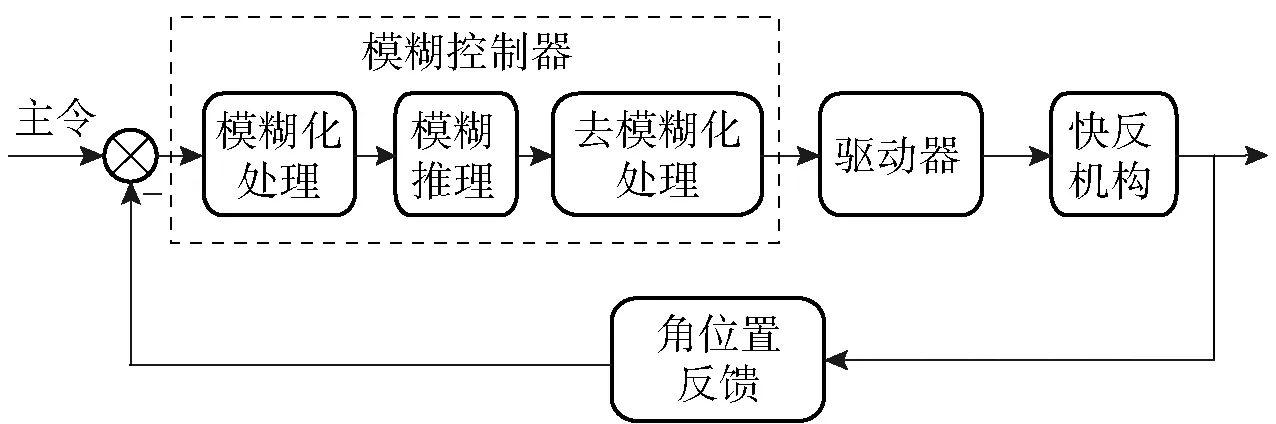
图4 快反镜模糊控制系统原理框图Fig.4 Functional block diagram of FSM fuzzy control system

1)将领域专家对快反镜的控制经验总结出“规则”，并将规则逐条排列构建知识库。按照前文的设计流程，通过将控制偏差和偏差变化率按照负大、负中、负小、零位、正小、正中、正大7个分类级别进行相应的模糊化处理，并按照知识库中的规则即模糊控制律进行模糊推理，就可获得需要的控制参数，该参数的获得过程是全自动的，也就自适应了对象模型参数的变化。上述7个分类级别的模糊化方法，对于绝大多数对象具有普适性。由此得到的控制器称为模糊控制器。快反镜伺服装置模糊控制系统原理框图如图4所示。

2)兼顾准确性及快速性，拟定模糊控制器为两输入三输出模式，并设定输入为e和ec，输出为Kp、Ki和Kd. 将e、ec、Kp、Ki、Kd按照前文所述分为7个级别，依次为NB(负大)、NM(负中)、NS(负小)、ZO(零位)、PS(正小)、PM(正中)、PB(正大)。并根据原理图4，得到整个模糊控制系统结构图，如图5所示。图5中，qe、qec为输入的量化因子，qp、qi和qd为输出的比例因子，E和EC分别为偏差及偏差变化率，KP、KI、KD分别为被控对象的比例、微分、积分3个被控参数。

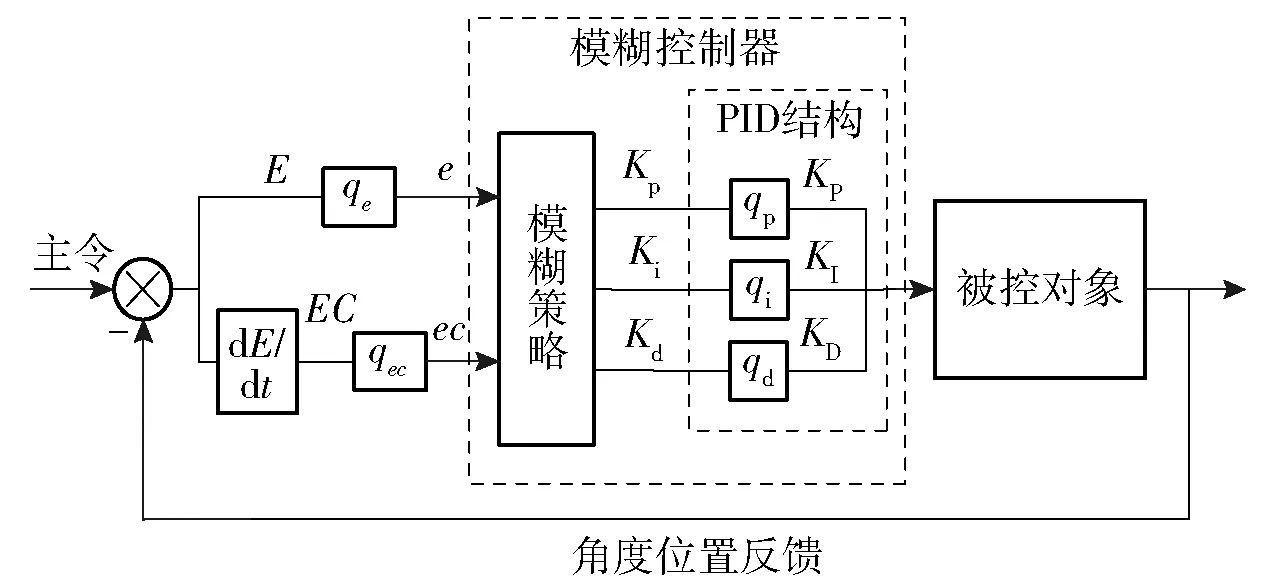
图5 模糊控制系统结构图Fig.5 Structure diagram of fuzzy control system

模糊控制器输入及输出的调整公式分别如(3)式和(4)式所示。

(3)

(4)

3.2 模糊化处理

根据模糊控制原理及控制器设计规则，设定模糊控制器的输入变量分别为e、ec，输出变量分别为Kp、Ki和Kd，输入变量的变化区间为[-6,6]，输出变量的变化区间为[1,13]，对应的论域为e,ec={-6,-4,-2,0,2,4,6},Kp,Ki,Kd={1,3,5,7,9,11,13}，并且设其模糊子集为

e,ec,Kp,Ki,Kd={NB,NM,NS,ZO,PS,PM,PB}.

qe、qec、qp、qi、qd数值在4.2节仿真实验中给出。输入变量及输出变量的隶属度函数均采用三角形隶属度函数[22]，如图6和图7所示，其纵坐标为隶属度，横坐标为域值。

图6 e、ec隶属度Fig.6 e, ec memberships

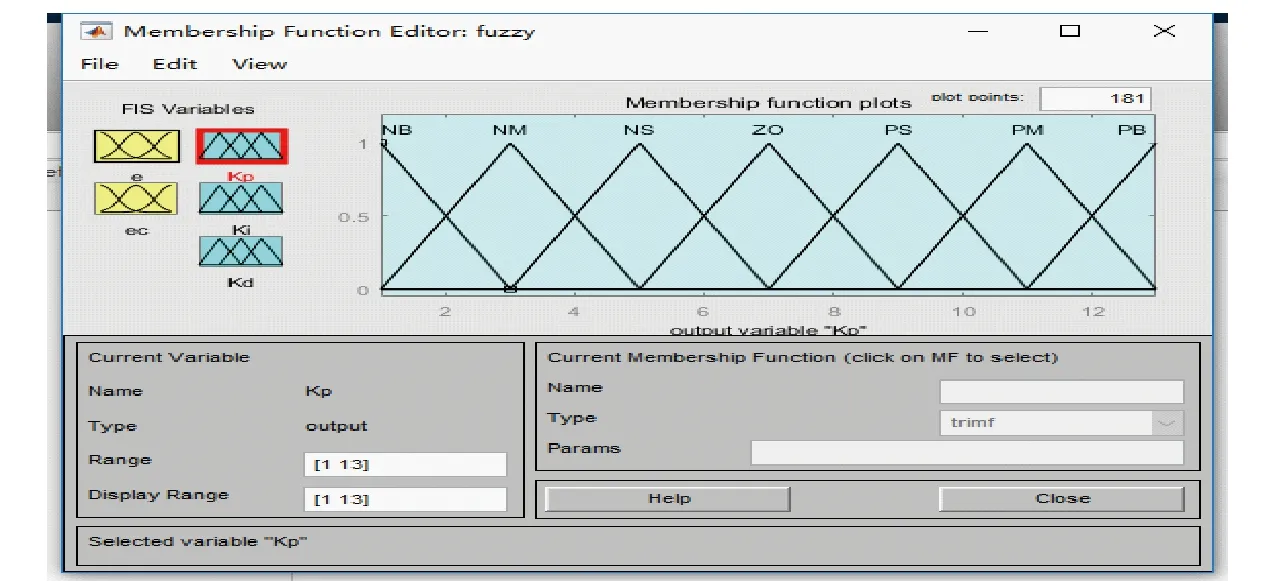
图7 Kp、Ki、Kd隶属度Fig.7 Kp, Ki, Kd memberships

3.3 模糊控制规则表的建立及模糊推理过程

根据模糊控制器Kp、Ki、Kd3个输出量在控制过程当中的作用及其变化后对控制性能不同影响的原理，针对快反镜的控制特点是“通过提高响应快速性来达到减小随动误差的效果”，特别对快反镜领域专家的工程调试经验研究总结后，确定Kp、Ki、Kd3个输出量的自整定原则如下[23-26]：

1)当输入e的幅值处于较大情况时，一方面为了提高系统的响应速度，另一方面为了避免系统初始时由于e突变增大进而产生的微分过饱和现象，控制变量参数Kp应取较大值，Kd应取较小值。同时为避免系统响应产生较大的超调现象，Ki要尽可能小；

2)当输入e和ec的幅值处于中等大小情况时，为了减小系统的超调量以及保证系统有较优的响应速度，Kp应保持在较小的状态；

3)当输入ec的幅值处于较小情况下，同样也就意味着整个系统趋于稳定时。此刻，为了保证系统有着良好的稳态性能，需将Kp、Ki的值增大，同时为避免输出响应产生振荡情况，应适当选取Kd的值。

参考以上自整定原则并综合专家的控制经验，建立如下模糊逻辑语句[27-28]：

1)if(eis NB) and (ecis NB) then (Kpis PB)(Kiis NB)(Kdis PS);

2)if(eis NB) and (ecis NM) then (Kpis PB)(Kiis NB)(Kdis NS);

3)if(eis NB) and (ecis NS) then (Kpis PM)(Kiis NM)(Kdis NB);

4)if(eis NB) and (ecis ZO) then (Kpis PM)(Kiis NM)(Kdis NB);

⋮

49)if(eis PB) and (ecis PB) then (Kpis NB)(Kiis PB)(Kdis PB).

由以上模糊逻辑语句可以得到如下关于Kp、Ki、Kd的模糊规则如表1、表2、表3[29-30]所示。

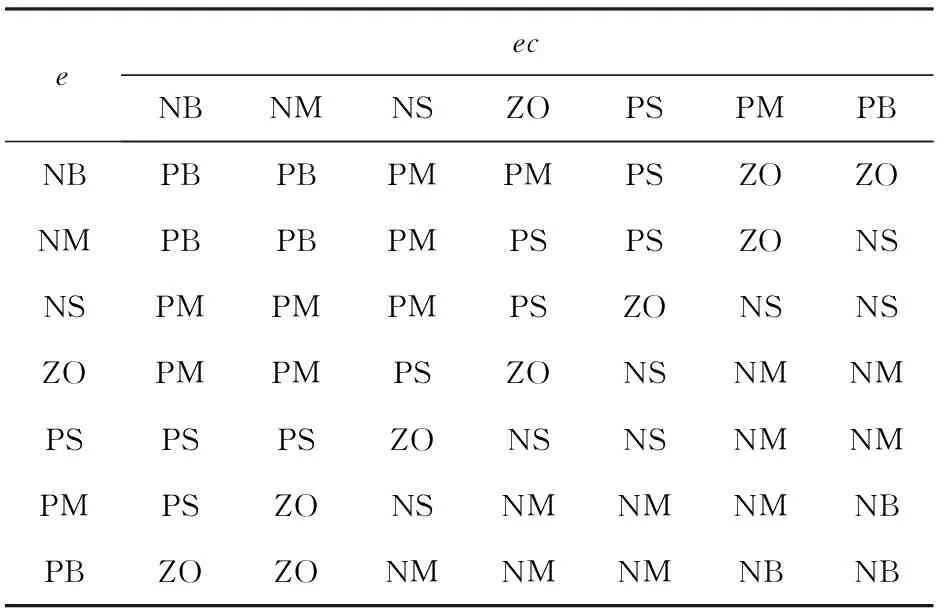
表1 Kp模糊规则表Tab.1 Kp fuzzy rules

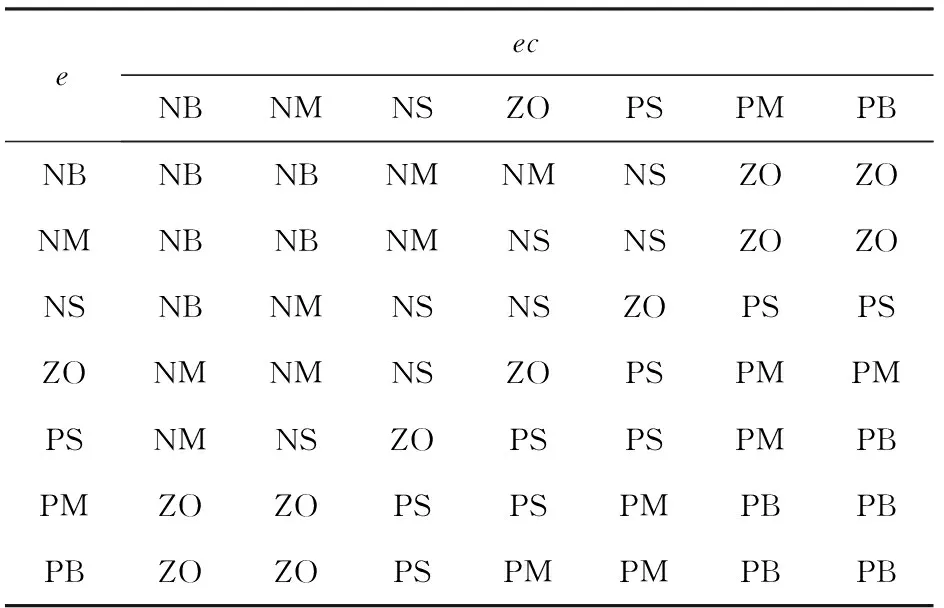
表2 Ki模糊规则表Tab.2 Ki fuzzy rules

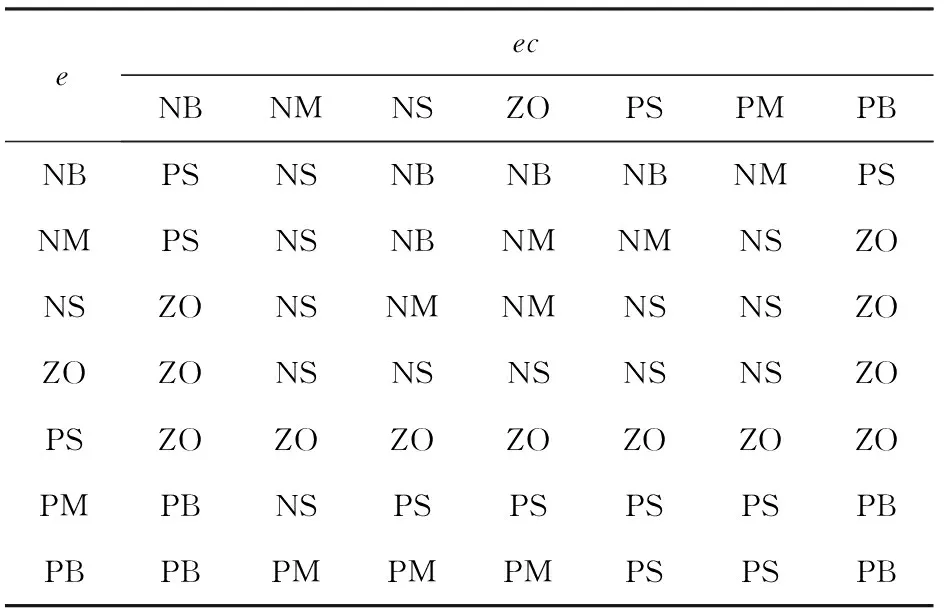
表3 Kd模糊规则表Tab.3 Kd fuzzy rules

3.4 去模糊化处理

通过以上模糊推理得到的是前文所述基于7个分类级别的模糊控制量，而整个控制系统中实际作用于被控对象的是精确控制量，因此需要将模糊控制量转换为精确控制量。综合考虑，本文采用了重心法[31]来进行去模糊化处理。具体方法如(2)式、(4)式所示。

4 系统仿真分析

4.1 仿真实验目的及内容

为了验证提出的模糊控制策略对提升快反镜伺服性能的有效性，以基于高频摇摆电机的快反镜为应用对象设计了模糊控制器，开展了采用模糊控制器的快反镜与基于传统PID控制快反镜对比仿真实验。仿真实验根据复合轴系统应用背景的需求，主要就以下4个方面的性能进行了对比研究：

4.1.1 阶跃输入响应性能

稳定裕量是控制系统工作的前提条件，所以仿真实验首先考查阶跃响应的超调等过渡过程指标。

4.1.2 抑制带宽

对于复合轴跟踪的应用背景，快反镜用于抑制主轴的残差。抑制带宽是衡量残差抑制能力的核心指标，因此仿真实验中计算了两类控制系统伺服回路的抑制带宽作为性能优劣的理论判据。

4.1.3 正弦输入响应性能

比较在典型正弦激励下两类控制系统的随动误差大小。

4.1.4 随机输入响应性能

使用多阶谐波信号叠加来模拟实际残差输入的随机特性，仿真比较在该激励信号作用下两类控制系统的随动误差，作为对抑制带宽理论评判结果的综合印证。

4.2 仿真模型及相关对象参数

高频摇摆电机是一类特殊的有限转角无刷力矩电机，拥有力矩电机所固有的转动范围大、负载能力强的基本特性；同时通过电机本体与负载反射镜结构一体化设计的方式，大大提高了装置的结构谐振频率，使其具有高频摇摆的可能，配合高精度的测角反馈和相应的控制算法，可达到高动态、高精度的控制性能，从而可作为大负载快反镜的驱动执行元件。仿真实验中采用的基于高频摇摆电机的快反镜其负载质量约1 kg，转动惯量达10-3kg·m2量级，对象等效传递函数见(5)式。

(5)

在MATLAB/Simulink里搭建好基于模糊控制与基于传统PID控制的快反镜系统仿真模型，如图8所示。图8中：基于高频摇摆电机的快反机构等效传递函数(FSM1、FSM2)为(5)式；PA1、PA2为线性功放驱动器，用放大倍率表示；传统PID控制器采用临界灵敏度法整定控制参数，得到PID参数分别为p=14，i=1 300，d=0.004 5；fuzzy controller详细设计结果见第3节中具体内容，其量化因子取值为qe=2 400，qec=2，比例因子取值为qp=10，qi=200，qd=0.015；angle1、agnle2为角位置反馈，取值考虑入射光线偏转与镜面机械偏转角之间的关系；仿真模型中设置了快反镜角位置(FSM angle position)和随动误差(FSM servo error)两个输出观测点。

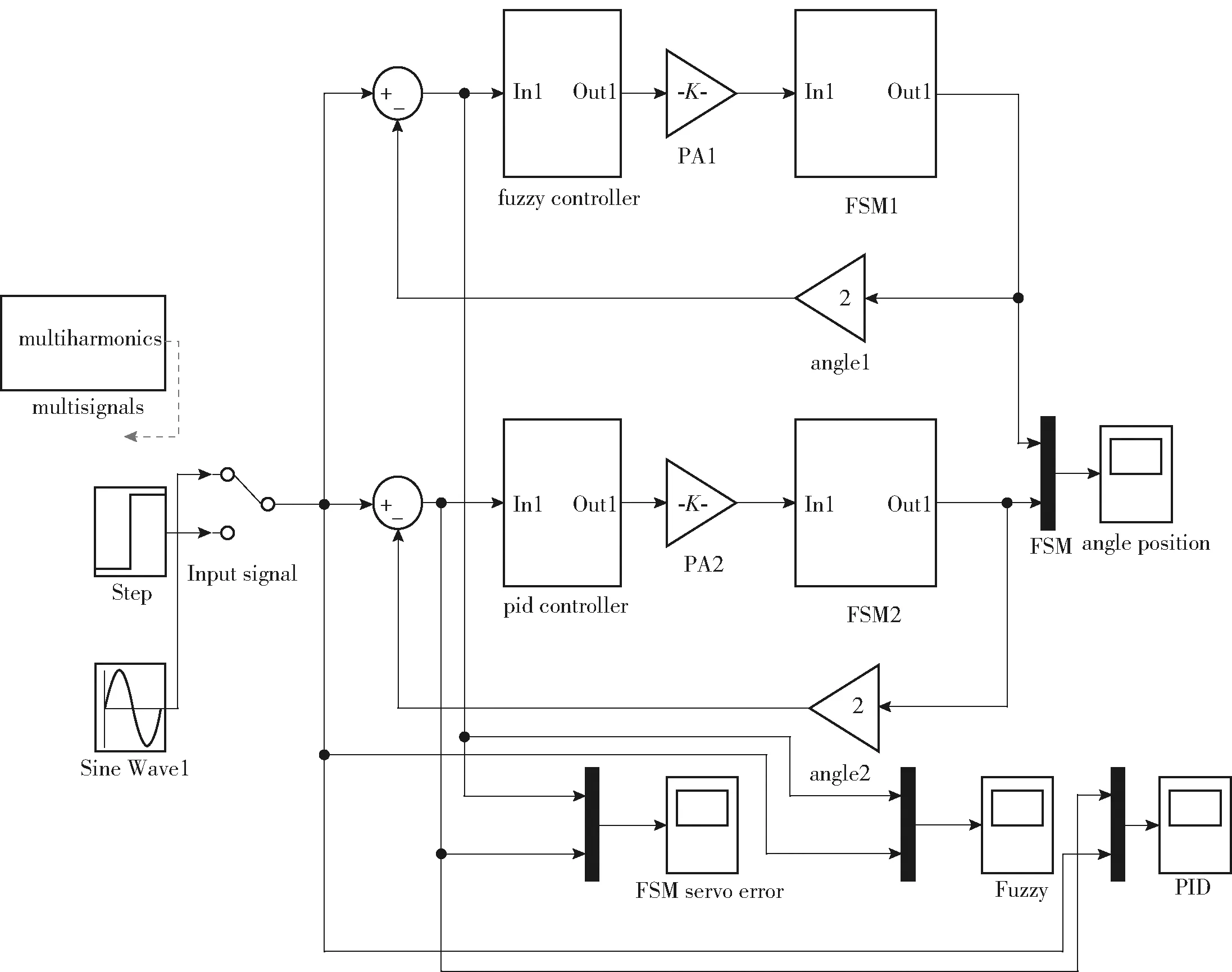
图8 模糊控制与PID控制系统仿真模型图Fig.8 Simulation model of fuzzy control and PID control system

4.3 阶跃输入响应性能对比仿真

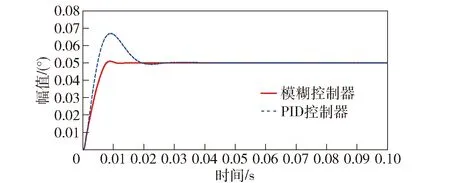
图9 模糊控制与PID控制快反镜阶跃响应曲线对比Fig.9 Step response curves of FSM by fuzzy control and PID control

在仿真模型中施加阶跃激励信号，比较模糊控制与PID控制下快反镜角位置输出的阶跃响应曲线，如图9所示。

依据图9不同的输出波形，对比分析可得两个系统阶跃响应性能指标，在表4中给出。由表4可以看出，模糊控制器与PID控制器相比，其调节时间更短，更快进入稳态，而且超调量非常小，无振荡。

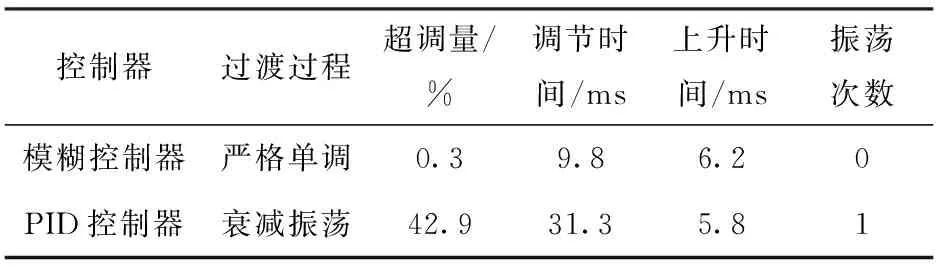
表4 两种控制器阶跃响应性能对比Tab.4 Comparison of step response performances oftwo controllers

4.4 抑制带宽计算及对比仿真

抑制带宽具体计算方法[32]如下：

设置输入正弦信号的幅值Ai，频率fi，测量随动误差的幅值Bi，则抑制比ki的计算公式为

(6)

式中：ki为当输入信号频率为fi时的抑制比；Bi为当输入信号频率为fi时随动误差幅值(″)；Ai为当输入信号频率为fi时输入信号的幅值(″)；i为当前测试的序次数，i=1,2,3,…,n.

当ki≈1时，此时的输入信号频率值fi则为快反镜伺服回路的抑制带宽。

通过数次仿真实验，ki逐步增大，直到逼近1时，得出如表5实验结果(特别说明，仿真实验幅值采用的单位统一为(°)，表格将(°)换算成(″)，输入幅值均为Ai=72″)。

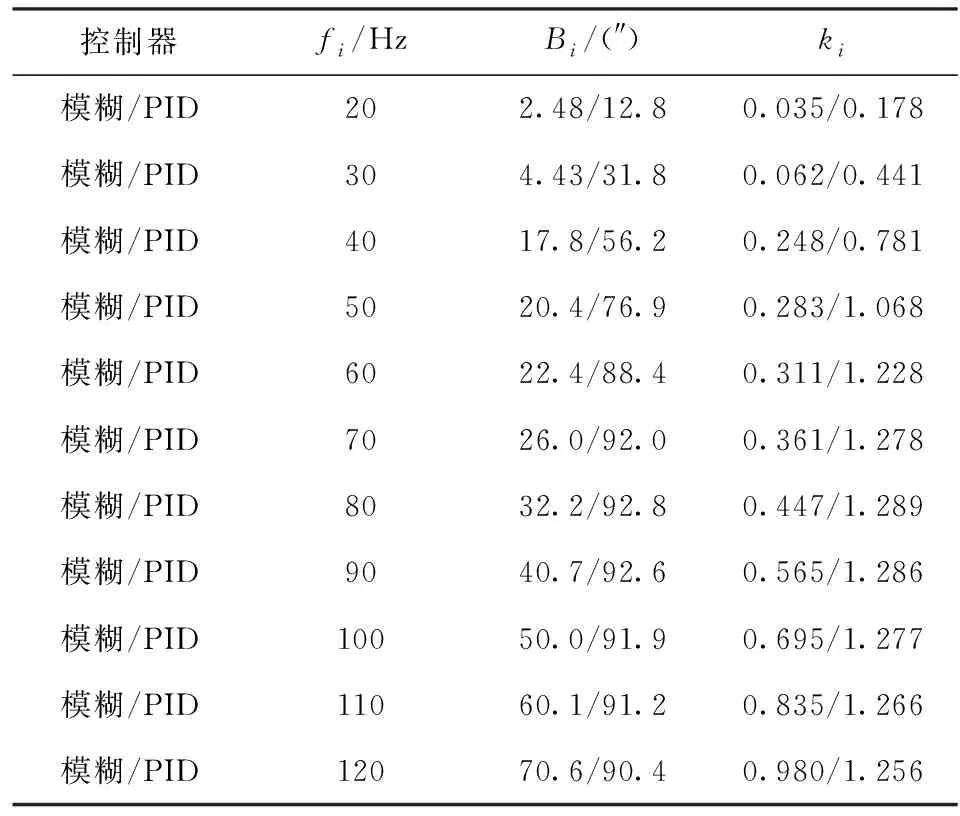
表5 不同频率下两种控制器的抑制比对比Tab.5 Suppression ratios of two controllers at differentfrequencies

4.4.1 实验结果1

从表5看出，当fi=50 Hz时，PID控制器的抑制比kfi=1.068≈1，此时两种控制器下随动误差的仿真结果分别如图10和图11所示。

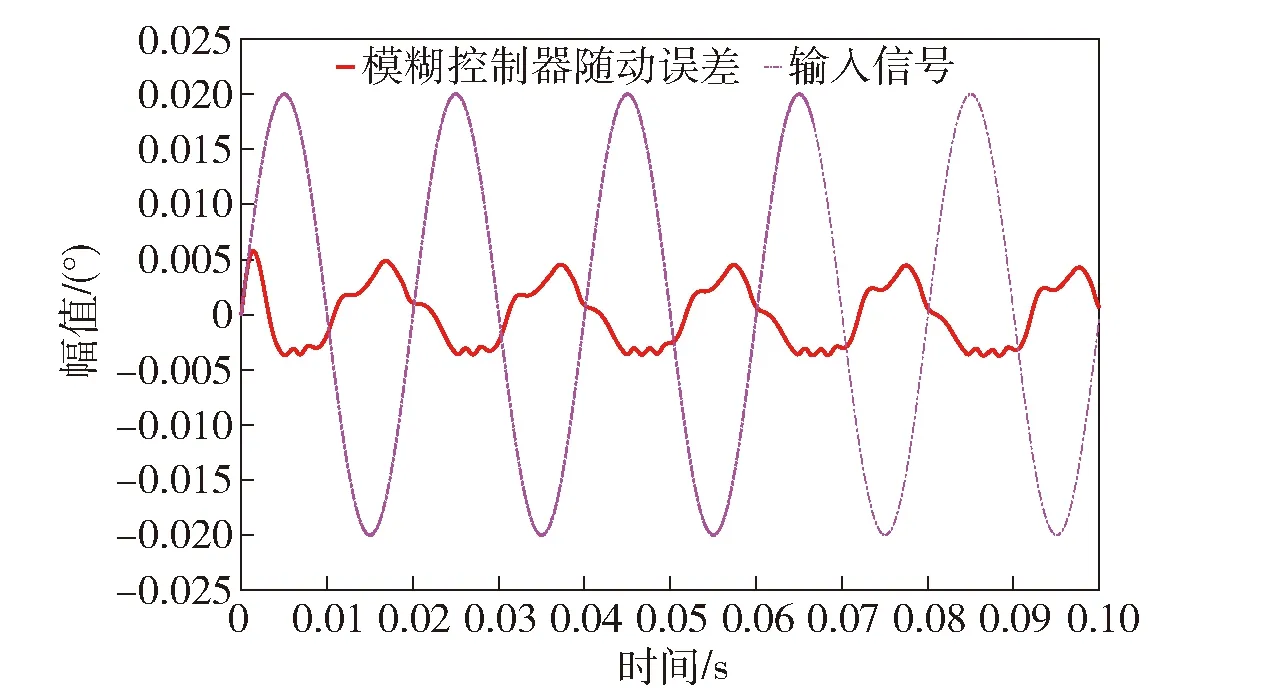
图10 模糊控制器下输入信号与随动误差的 幅值比较(fi=50 Hz)Fig.10 Amplitudes of input signal and E at the input signal frequency of 50 Hz under the control of fuzzy controller

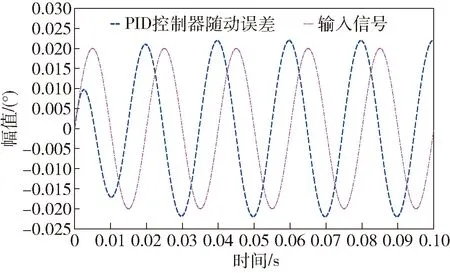
图11 PID控制器下输入信号与随动误差的 幅值比较(fi=50 Hz)Fig.11 Amplitudes of input signal and E at the input signal frequency of 50 Hz under the control of PID controller

4.4.2 实验结果2

从表5看出，当fi=120 Hz时，模糊控制器的抑制比ki=0.980 0≈1，此时两种控制器下随动误差的仿真结果分别如图12和图13所示。

图12 模糊控制器下输入信号与随动误差的 幅值比较(fi=120 Hz)Fig.12 Amplitudes of input signal and E at the input signal frequency of 120 Hz under the control of fuzzy controller

通过实验结果1和实验结果2可以看出：采用传统PID控制器，系统抑制比ki≈1时，其抑制带宽为fi=50 Hz；而采用模糊控制器，当系统抑制比ki≈1时，其抑制带宽为fi=120 Hz. 由此可得出结论，采用模糊控制系统的抑制带宽远高于采用传统PID控制的抑制带宽，因此模糊控制非常适合用于复合轴跟踪应用的快反镜伺服系统。

4.5 正弦输入下性能对比仿真

输入频率为10 Hz、幅值为0.02°的正弦信号，可得出模糊控制误差曲线与PID控制系统误差曲线对比，如图14所示。

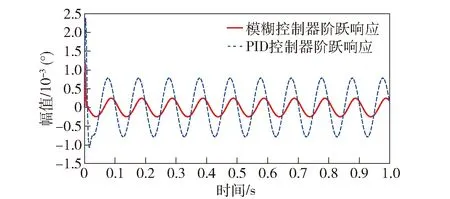
图14 模糊控制器误差曲线与PID控制器误差曲线对比Fig.14 Error curves of fuzzy controller and PID controller

依据图14两控制器误差曲线图分析可得：模糊控制最大误差为0.453 6″，PID控制最大误差为2.955 6″，模糊控制相对于PID控制，误差明显减小。

4.6 随机输入性能对比

4.4节的仿真实验结果表明：采用模糊控制器的快反镜，其抑制带宽显著高于采用传统PID控制器的快反镜；本节通过多次谐波叠加的方式构造激励信号，模拟复合轴系统实际工况下的残差随机特性，比较在随机输入下两种控制系统的快反镜误差特性，对抑制带宽理论评判结果进行综合印证。

根据对某型复合轴系统主轴残差频谱特性的分析结果，构造如下激励信号模拟残差的随机特性：

输入信号=谐波1+谐波2+谐波3，其中：1)谐波1为1 Hz、0.1°正弦信号；2)谐波2为10 Hz、0.02°正弦信号；3)谐波3为40 Hz、0.005°正弦信号。

当输入激励为上述多次谐波信号叠加构成时，可得出模糊控制系统误差曲线与PID控制系统误差曲线对比，如图15所示。

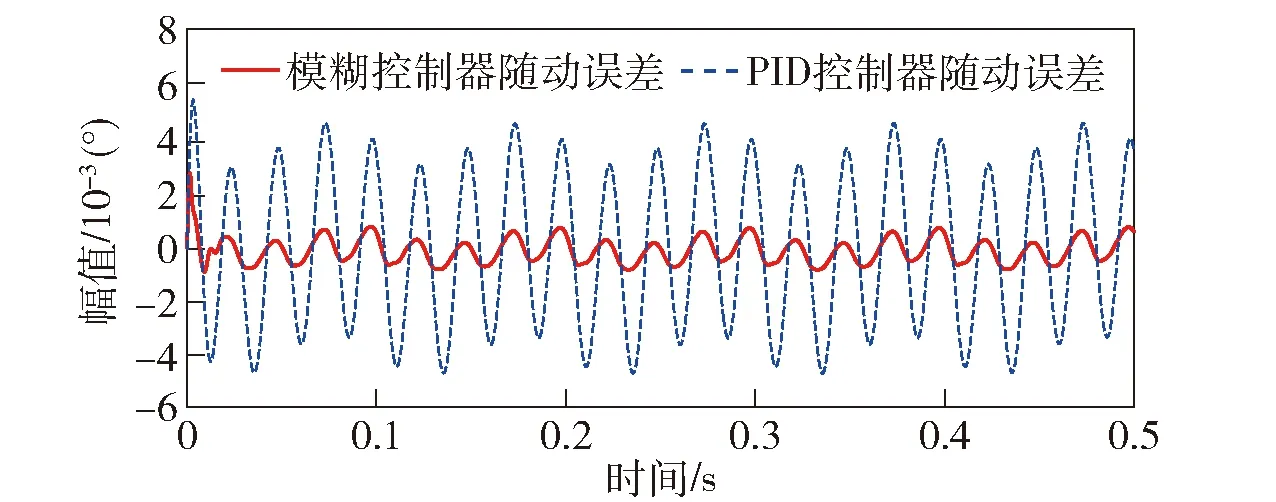
图15 模拟随机输入信号下模糊控制器与PID控制器误差曲线对比Fig.15 Error curves of fuzzy controller and PID controller in case of random input signals

根据图15两误差曲线图分析可得：模糊控制稳态误差均方根为1.620″，PID控制稳态误差均方根为12.996″，模糊控制在输入为随机信号时，性能明显优于PID控制。该结果与抑制带宽的计算结果相吻合。上述随机输入信号中最高频率分量为40 Hz，而模糊控制系统的抑制带宽约为120 Hz，远远高于输入信号频率，所以能很好地抑制输入信号扰动；而对照PID控制系统，其抑制带宽约为50 Hz，几乎与输入的最高频率持平，故不能有效抑制输入扰动，随动误差呈数量级上升。

5 结论

针对高品质控制要求下传统PID控制器的局限性，本文提出将模糊控制策略与PID相结合设计快反镜伺服控制器，并以基于高频摇摆电机的快反镜为应用对象进行了模糊控制器的设计实现。通过抑制带宽计算、阶跃输入、正弦输入、随机输入下伺服性能与基于PID控制的快反镜系统对比，表明了采用模糊控制器的快反镜有着响应速度更快、无超调和震荡现象、随动误差更小、抑制带宽显著增加等优势。由于本文的研究目的是提高快反镜伺服性能来优化残差抑制能力，最终通过构造实际工况下的残差随机输入，比较模糊控制器与传统PID控制器的不同效果，验证了模糊控制器残差抑制能力更显著优于传统PID控制器，尤其适合作为子轴应用于高精度复合轴跟踪系统，在诸如战术激光武器等要求跟瞄精度达到微弧度量级的光束定向场合具有巨大的应用潜力。

但是，由于模糊控制算法的独特性，其控制效果相当依赖专家的控制经验，因此不仅会导致跟踪精度、响应速度受限于有限的控制经验，也会导致同样的模糊控制算法在不同驱动方式的快反镜上控制效果存在差异的问题。随着机器学习的不断发展，这一问题也有了解决途径，通过机器学习可以不断积累不同情况下的控制经验，并根据实际工作情况筛选最优控制经验，从而使知识库和模糊推理规则不断更新和完善，因此可以显著提升模糊控制的控制性能，届时模糊控制将会广泛适用于各类快反镜控制系统。