接触式轮廓仪的自动标注数学模型

崔煜

摘要：为2020年全国大学生数学建模竞赛D题提供可行解法，针对探针沾污、探针缺陷、扫描位置不准导致的轮廓仪数据不准问题，利用matlab对数据进行分段处理，进而确定水平线轴线，拟合曲线段，斜线段，确定交点坐标、利用基本的数学知识建立模型求解出工件直线段各个参数，用最小二乘法拟合和圆弧。针对有倾斜角的工件测量数据，利用旋转变换法将有倾斜角度的工件测量数据水平校正。

关键词：数据拟合;标注;最小二乘法;旋转变换

1.问题的提出

轮廓仪是一种两坐标测量仪器，它由工作平台、夹具、被测工件、探针、传感器和伺服驱动等部件组成。其工作原理是，探针接触到被测工件表面并匀速滑行，传感器感受到被测表面的几何变化，在X和Z方向分别采样，并转换成电信号。该电信号经放大等处理，转换成数字信号储存在数据文件中。

轮廓曲线理想状况下是光滑的，但由于接触式轮廓仪存在探针沾污、探针缺陷、扫描位置不准等问题，呈现出粗糙不平的情况，这给工件形状的准确标注带来影响。

因此简化问题，假设被测工件的轮廓线是由直线和圆弧构成的平面曲线（见图4）。请建立数学模型，根据附件1（工件1的水平和倾斜测量数据）、附件2～附件4（工件2的多次测量数据）所提供的轮廓仪测量数据，研究下列问题：

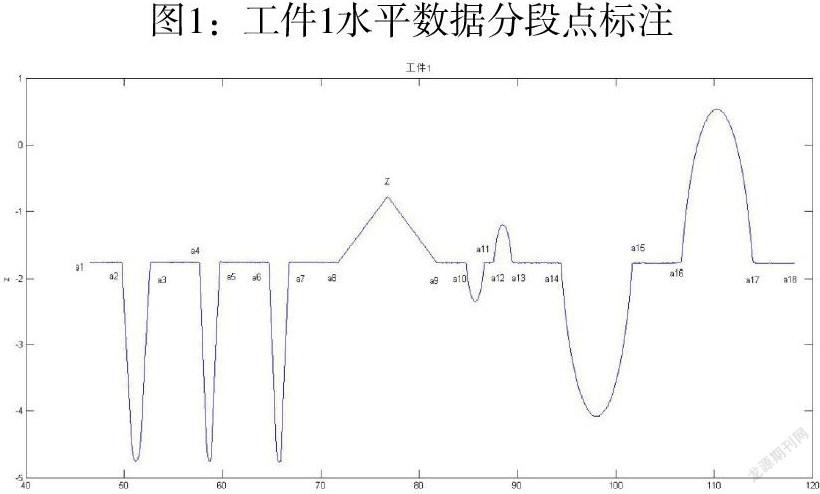
问题1是根据附件1中的工件1在水平状态下的测量数据即表level，其轮廓线如图4所示，请标注出轮廓线的各项参数值：槽口宽度、圆弧半径、圆心之间的距离、圆弧的长度、水平线段的长度、斜线线段的长度、斜线与水平线之间的夹角和人字形线的高度。

问题2是在同一工件在不同次测量时，由于工件放置的角度和位置不同，轮廓线参数的计算值也会存在差异。附件1中的表down给出了工件1在倾斜一个角度和有一些水平位移状态下轮廓线的测量数据。请计算该工件测量时的倾斜角度，并作水平校正。在数据校正后，完成问题1的任务，并比较两种测量状态下工件1各项参数计算值之间的差异。

2.数据处理

通过初步分析，发现附件1中原始较为完整，不存在缺失和重复，数据精度比较高，到小数点后九位。而matlab中精度是小数点后四位，所以采用excel进行计算，采用matlab进行画图。

将工件1中level表格的数据导入matlab，利用画图函数可得如下图1，为了更清楚明确的计算各个参数，分别在图中标注了各个分段点，同时也将数据按点分段。

通过图1可以看到水平线段有8段，圆弧有7段，人字高数据一段。

3.问题一模型的建立与求解

3.1模型的建立

由于工件1轮廓线中水平线在放大后粗糙凹凸不平，不能够直接从图形中选取分段点。假设工件水平面光滑，统计数据分析，拟合各个水平线段的直线方程。再与各个曲线拟合的方程联立求解得出交点。

1、对于水平线，求8段数据的平均数

其中为第段水平数据段的平均值。

2、对于斜线建立直线模型

其中对于参数的设定用数据拟合方法。

3、由于水平线上拐角处凹凸不平，很难确定端点坐标，同时为了较为准确合理的求出工件的水平长度、夹角，利用曲线拟合数据来计算端点，对于每一条弧线假设满足方程：

4、类似中学数学中求点的坐标的方法，分别联立水平线和2条斜线方程

解方程可得的坐標。

5、类似中学数学中求点的坐标的方法，分别联立水平线和曲线方程

解方程可得的横坐标。

6、因此可以计算得出槽口宽度

7、为了方便求出夹角，三个铅笔轮廓与水平线相交的上部分近似的看成直线段，拟合出直线段的直线方程

8、铅笔轮廓上半段直线、斜线与水平线之间的夹角的正切为，则斜线与水平线之间的夹角为

9、斜线的方程（2）已给出，假设斜线段是直线斜线，其长度为

10、对于工件中圆弧部分要求出圆心和半径，建立圆的方程

下面我们采用最小二乘法来进行拟合[5]，因此设最小二乘圆的一般方程为

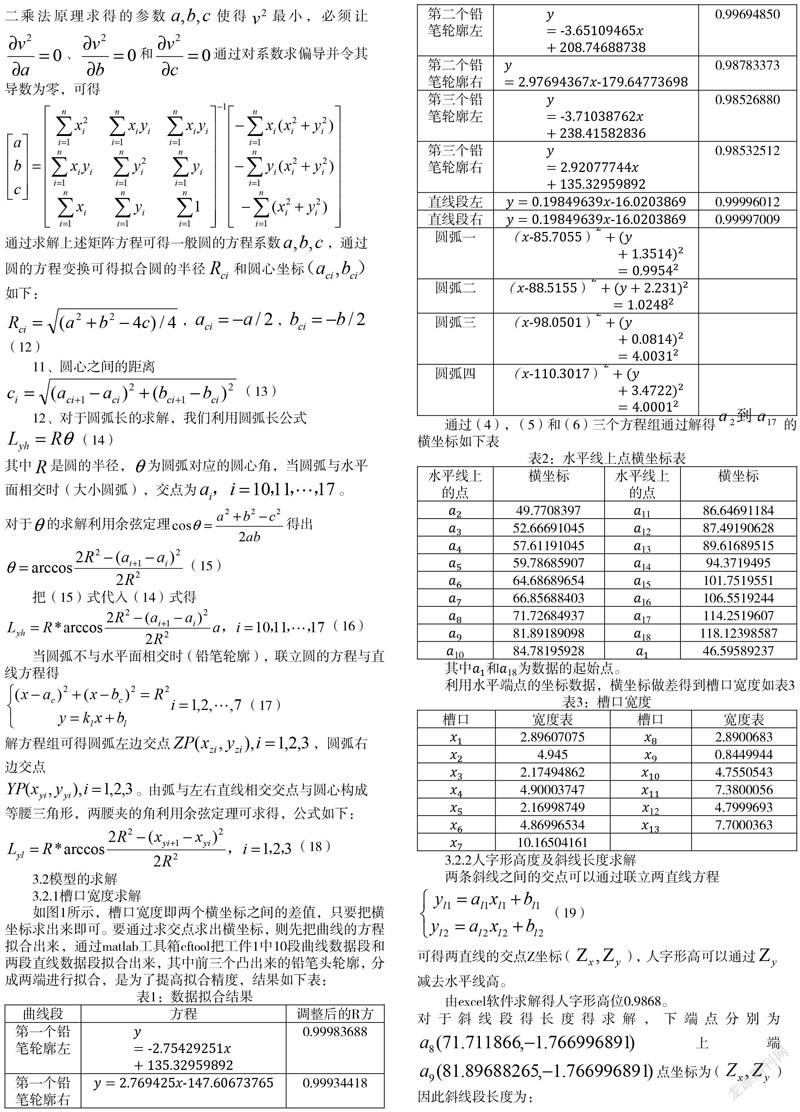
拟合误差的平方和为由最小二乘法原理求得的参数使得最小，必须让、和通过对系数求偏导并令其导数为零，可得

通过求解上述矩阵方程可得一般圆的方程系数，通过圆的方程变换可得拟合圆的半径和圆心坐标如下：

11、圆心之间的距离

12、对于圆弧长的求解，我们利用圆弧长公式

其中是圆的半径，为圆弧对应的圆心角，当圆弧与水平面相交时（大小圆弧），交点为。

对于的求解利用余弦定理得出

当圆弧不与水平面相交时（铅笔轮廓），联立圆的方程与直线方程得

（17）

解方程组可得圆弧左边交点，圆弧右边交点

由弧与左右直线相交交点与圆心构成等腰三角形，两腰夹的角利用余弦定理可求得，公式如下：

3.2模型的求解

3.2.1槽口宽度求解

如图1所示，槽口宽度即两个横坐标之间的差值，只要把横坐标求出来即可。要通过求交点求出横坐标，则先把曲线的方程拟合出来，通过matlab工具箱cftool把工件1中10段曲线数据段和两段直线数据段拟合出来，其中前三个凸出来的铅笔头轮廓，分成两端进行拟合，是为了提高拟合精度，结果如下表：

通过（4），（5）和（6）三个方程组通过解得的横坐标如下表

其中和为数据的起始点。

利用水平端点的坐标数据，横坐标做差得到槽口宽度如表3

3.2.2人字形高度及斜线长度求解

两条斜线之间的交点可以通过联立两直线方程

可得两直线的交点Z坐标（），人字形高可以通过减去水平线高。

由excel软件求解得人字形高位0.9868。

对于斜线段得长度得求解，下端点分别为上端点坐标为（）因此斜线段长度为：

3.2.3斜线与水平线之间的夹角求解

为了简化计算，将三个铅笔轮廓与水平线相交的上部分近似的看成直线段，数据上选取部分数据作直线拟合，而对于斜线段直接选取数据拟合，求出得8条直线方程、斜率和斜倾斜角如下表：

3.2.4圆心、圆的半径及弧长的求解

首先由最小二乘法拟合出圆的方程如下表

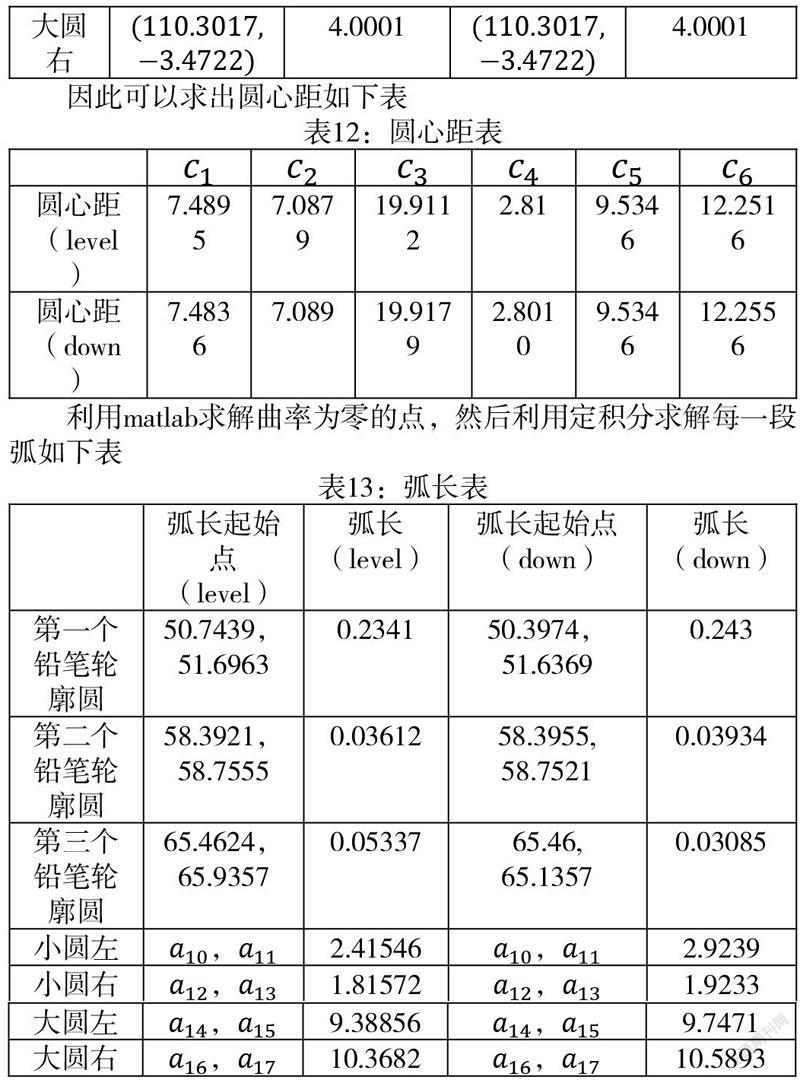
因此可以求出圆心距如下表

利用matlab求解曲率为零的点，然后利用定积分求解每一段弧如下表

4.问题二模型的建立与求解

4.1模型的建立

附件1中的表down给出了工件1在倾斜一个角度和有一些水平位移状态下轮廓线的测量数据，计算该工件测量时的倾斜角度，并作水平校正。

对于工件1倾斜角角度的求解，从图形中选取斜线段设

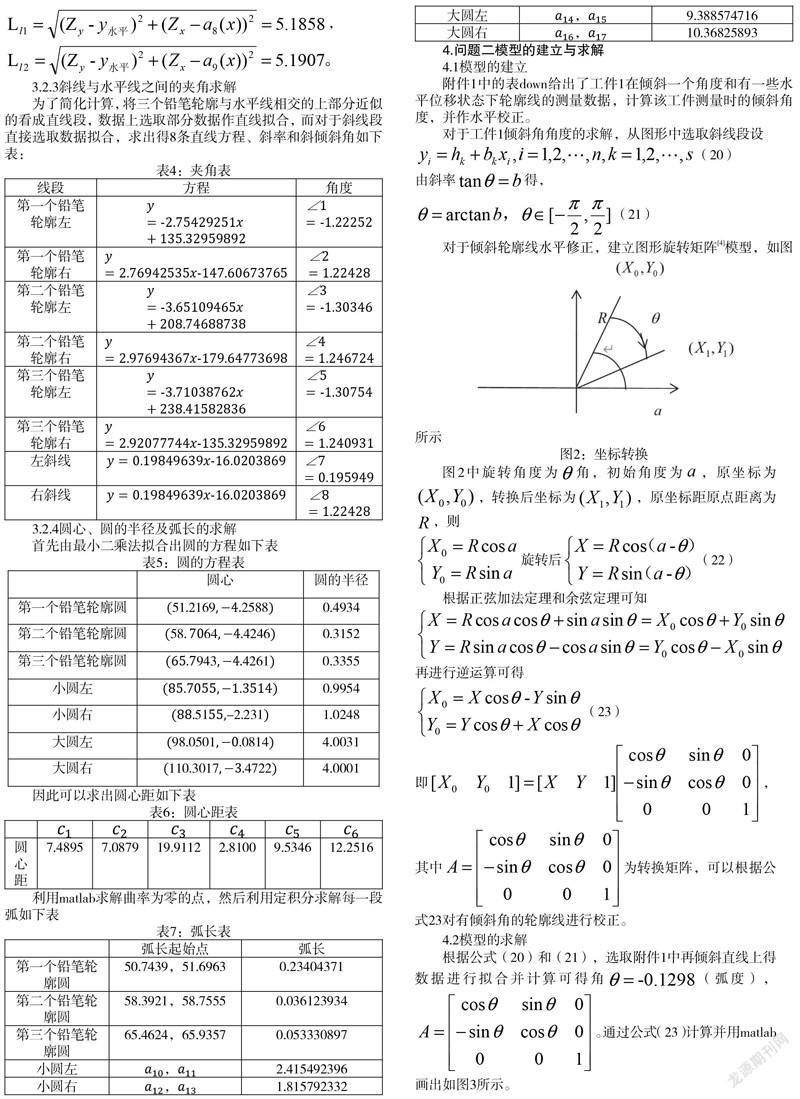
对于倾斜轮廓线水平修正，建立图形旋转矩阵[4]模型，如图所示

图2中旋转角度为角，初始角度为，原坐标为，转换后坐标为，原坐标距原点距离为，则

根据正弦加法定理和余弦定理可知

再进行逆运算可得

即，其中为转换矩阵，可以根据公式23对有倾斜角的轮廓线进行校正。

4.2模型的求解

根据公式（20）和（21），选取附件1中再倾斜直线上得数据进行拟合并计算可得角（弧度），。通过公式（23）计算并用matlab画出如图3所示。

在数据校正后，采用与问题一同样的计算方法，对上图中的轮廓线相关参数进行求解。求得的结果与图一中相关数据进行对比。

4.2.1槽口宽度

先对斜线，圆弧进行数据拟合，然后通过直线的方程和圆的方程计算出端点的横坐标。

利用水平端点的坐标数据，横坐标做差得到槽口宽度如表3

4.2.2人字形高度及斜线长度求解

由excel软件求解得。对于斜线段的长度得求解，下断点分别为，上端点坐标为（）因此斜线段长度为：，。

4.2.3斜线与水平线之间的夹角求解

为了简化计算，将三个铅笔轮廓与水平线相交的上部分近似的看成直线段，数据上选取部分数据作直线拟合，而对于斜线段直接选取数据拟合，求出得8条直线方程、斜率和斜倾斜角如下表：

4.2.4圓心、圆的半径及弧长的求解

首先由最小二乘法拟合出圆的方程如下表

因此可以求出圆心距如下表

利用matlab求解曲率为零的点，然后利用定积分求解每一段弧如下表

5.结论

本文对探针沾污、探针缺陷、扫描位置不准等问题带来的数据不准问题，建立数学模型对工件形状相关参数准确标注，建立模型所运用的数学知识简单易懂，计算方法简单易行。对于圆弧圆的半径和圆心的求解，利用最小二乘法拟合，较为理想的确定圆的半径和圆心，提高数据的准确性，实现轮廓线自动标定。对于有倾斜一个角度的工件数据，采用旋转变换实现数据调整为正常状态。

参考文献：

[1]赵琦，解琳琳，侯妙乐，刘浩宇.基于点云数据的雀替轮廓线参数信息自动化提取方法[J].地理信息世界，2018年，第25卷第5期

[2]韩志国，李锁印，冯亚南，赵琳.接触式轮廓仪探针状态检查图形样块的研制[J]，微电子技术，2019年第9期

[3]陈十进，刘瑾，杨海马，刘海珊，韦钰，肖俊，解光耀.非接触式钢轨三维轮廓参数检测系统研究[J].仪表技术与传感器，2019年第5期

[4]闫志刚，图形学中绕任意轴旋转矩阵的推广[J].计算机时代，2009年第12期

[5]杨旭东，大量程轮廓综合测量系统研究[J].华中科技大学博士论文.2007年5月

[6]司守奎，孙兆，数学建模算法与应用[M].国防工业出版社.2015年4月（第二版）

[7]姜启源，数学模型[M]，高等教育出版社，2008年3月（第三版）

（浙江交通职业技术学院 人文学院 杭州 311112）