初中数学教学中数形结合思想的应用

李彪

摘要：学生想要学好一门学科知识，应该具备良好的学习思想，以有思想、有步骤地探究知识、掌握知识。其中，初中数学是学生必修的一门学科知识，也是学生学习其它课程知识的基础，但从以往学生的学习情况来看，仍有不少学生缺乏学习思想，探究知识缺乏计划性和目的性。因此，本文从初中数学教学中应用比较普遍的数形结合思想出发，结合有关的初中数学知识，具体谈谈如何应用数形结合思想，使得学生可以利用有用的数学思想来探究数学问题。

关键词：初中数学;数形结合;问题;分析

前言

通常很多学生面对复杂、抽象的数学问题往往束手无策，无法寻找到解答数学问题的突破口，浪费了大量的时间和精力，这与学生缺乏良好的数学思想有关。如果学生具备良好的数学思想，则有利于其有条理的分析问题、寻找问题中可用的条件。那么在初中数学教学中，数形结合是一种应用较为广泛的数学思想，它实现了数与形的相互转换，将抽象的数学知识及问题具体化。

一、数形结合思想的概念及应用原则

（一）概念

与其它数学思想相比，数形结合思想更加直观和清晰，它主要是将抽象的数量关系与形象的图形结合起来，以实现数量与图形的相互转换，从而对抽象的知识与问题具体化、简单化，从而帮助学生理解和掌握数学知识的一种有效数学思想方法。

（二）应用原则

在初中数学教学中，应用数形结合思想展开数学知识的教学，应该遵循等价性、双向性、简单性等应用原则[1]。其中，等价性是指在应用数形结合时，应该注意代数性质与几何性质之间的等价关系，否则将无法做到运用图形来表现数量关系。双向性是指要求学生即要进行代数关系的探索，又要重视几何图形的分析，从而实现彼此的相互探索、相互转换，而不仅是“数”向“形”的转换。简单性则是数形结合思想的一个基本应用原则，它是指学生应该尽可能从简单的图形、构图方式着手，寻找“数”向“形”之间的转换关系，从而做到图形的简洁，进而促使数量关系变得清晰明了。

二、初中数学教学中数形结合思想的应用

（一）在初中数学函数中的应用

函数是初中数学的一个重要知识点，而且涉及到的数学问题也比较多，那么为了帮助学生正确理解和运用函数有关知识，教师应该适当应用数形结合思想，引导学生从数形结合角度，分析函数问题中存在的“数”与“形”关系，从而寻找到“数”与“形”相互转换的方式，从而顺利解答有关的数学函数问题。比如，学生遇到关于一次函数的应用问题时，则可以应用数形结合思想来展开问题的分析与探究，从而将所学的一次函数知识应用于实际问题的解答。

以初中数学函数为例，在解决如下函数问题：弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的重量x（kg）间有下面的关系：

那么弹簧不挂重物时，长度为多少？如果物体重6Kg，弹簧长度是否为13.5cm？

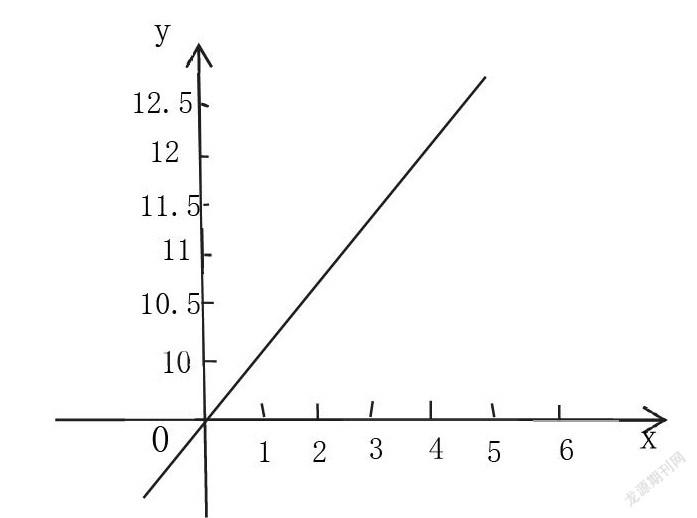
在进行解答过程中，教师可以引导学生应用数形结合思想，对题目所给的数量关系转化为具体的图形图象，从而直观、清晰地分析数量之间的关系，进而寻找到问题的解决方法。比方说，学生可以根据表格中所给的数字，绘制有关的一次函数图象，如下所示：

一方面，学生可以结合题目中所给的图表，另一方面也可以绘制如上的一次函数图象，从图表以及图象中，分析其中弹簧的长度y（cm）与所挂的物体的重量x（kg）的关系，从而做到数量与图形的相互转换，进而激发学生的数形结合思维，最终加深学生对一次函数图象的理解和认知。那么通过绘制出来的图象，学生可以直观地看到，当不挂物体时，也就是x为0，那么从表格和图象中，直接可以得出弹簧本身的长度为10cm。而从函数图象来看，x越大y就越长，所以6kg物体的弹簧长度要比5kg的物体要长。

（二）在初中数学几何中的应用

初中数学立体几何也是学生比较头疼和害怕的数学知识点，许多的立体几何问题比较抽象，对学生的空间思维和分析解答能力提出了很高的要求，而对于一些基础较弱的学生来说，他们往往不愿花费过多的时间去学习与探究立体几何问题，这不利于提升学生的数学思维能力。那么在实际教学中，教师应该利用有效的数学思维方法，有意識地引导学生展开立体几何问题的探究，使其真正理解和掌握几何知识[2]。首先，在进行初中数学几何有关内容教学时，教师可以引导学生分析一些难度不大的几何数学问题，以从简单的问题开始，逐步引导学生运用数形结合思想来深究几何问题，从而引导学生树立起学习的信心。

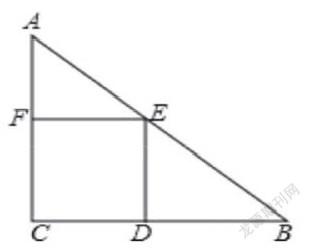
以初中数学有关几何问题为例，如下这道问题：在Rt△ABC中，斜边AB的长为35厘米，边长为12厘米的正方形CDEF内接于△ABC，求△ABC的周长为多少厘米？

其中，根据此几何题目，教师可以引导学生将几何问题转化为熟悉的“一元二次方程”问题，从而实现以“形”化“数”，进而寻找到二则存在的关系，最终寻找到几何问题的突破口。比方说，教师可以引导学生从相似三角形和勾股定理等已学的数学知识点出发，分析题目中所给的信息是否可以创建相关的数量关系。那么根据题目，△ABC是一个直角三角形，正方形CDEF内接于△ABC，而由正方形和直角三角形的性质，可以得知Rt△AFE∽Rt△ACB。这时学生可以进一步创建数量关系，如FE/CB=AF/AC。如果假设BC=a，AC=b，根据勾股定理得a2+b2=352=1225，那么FE/CB=AF/AC就得12/a=（b-12）/b，进一步化简得12（a+b）=ab。学生继续到这一步，似乎没有了头绪，不懂得如何再建立起数量关系，这就需要教师给予适当引导，让学生往一元二次方程角度思考，创建（a+b）2=a2+b2+2ab的关系，并化简得到（a+b）2=1225+24（a+b），那么如果将a+b看作一个整体，则可以得到a+b=49，最后求出△ABC的周长。

三、结语

综上所述，数形结合依然是初中数学教学中的一个重要思想，对学生分析与探究数学知识起到重要的指导作用。而在本文中，主要将数形结合思想应用于函数、几何知识的教学，从而培养学生养成良好的数形结合思想。

参考文献：

[1]李莉.初中数学数形结合思想的探究[J].教育教学论坛，2017.4（25）：221-222.

[2]欧阳恭倩.浅谈数形结合在初中数学中的运用[J].未来英才，2017，2（23）：240-240.