学生为本,返璞归真
2020-09-10施志娟
施志娟
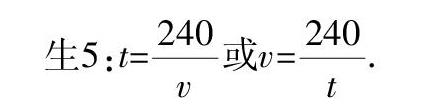
[摘 要] “以生为本、以学定教”是践行核心素养落地生根的关键,也是充分激活学生参与数学活动的关键,笔者在践行“合格课堂+”的过程中,坚持以生为本的理念,充分彰显合格课堂+的引领价值.
[关键词] 初中数学;合格课堂+;以生为本
新课改在我国实施了多年,各地积极响应号召,提出了各种新型的教学理念及教学方法. 课堂是发挥教学实效的主要载体,在不同的课堂改革理念应运而生的背景下,“改”决定了新型课堂的属性,我们不禁要思考:传统课堂教学究竟缺失了什么?教师的教缺失了哪些本源性问题?學生又缺失了什么?课堂的“改”需要回归什么?对此,我们需要让教学回归“原点”进行思考,学生最本质的属性是学习者,在学习过程中应占有主动地位,而教师的基本使命是教书育人,在这个过程中,育人比教书更重要. 因此,教师坚持教育的本质,引导学生变被动接受为主动学习是课改的本源问题. 在此基础上,专家们提出了以“限时讲授、小组合作、踊跃展示、及时反馈”16字为依据的“合格课堂”,将此与各个学科相结合,便形成了具有不同学科特色的新型课堂,即实现“合格课堂+”. 经过几年的实施与改进,“合格课堂+”在我市取得了较大成效,也在更大范围内得到了推广. 笔者结合常态课“19.1 变量与函数”(人教版八年级下册)的教学过程,就如何践行“合格课堂”与初中数学学科的“+”谈谈自己的理解.
自主学习,情境激发
自主先学是合格课堂体现学生主体性的途径之一,传统的自主先学是由学生对照书本预习,这样对学生掌握知识虽有一定的效果,但却不易激发学生的主动性,学生更多的是从书上获取到知识,而非自己有所发现. 合格课堂旨在回归教学的本质,因此教师创设一定的情境激发学生思考,让学生自己发现新知才是真正意义上的自主先学.
实例1 汽车在行驶过程中有哪些相关的量?
生1:汽车在行驶的过程中有路程(s)、速度(v)、时间(t)这三个量.
师:没错,如果汽车是匀速行驶,速度为v=80 km/h,现在我们规定数值始终不变的量为常量,数值发生变化的量为变量,那么,如何用式子来表示两个变量s,t之间的关系?
生2:s=80t或t=■.
师(追问):s=80t中,当t=1时,s的值为多少?有几个值与之对应?
生3:当t=1时,s=80,即当t取定一个值时,s都有唯一的值与之对应.
师(追问):若汽车从我市开到南京,路程s=240 km,其中常量、变量分别是哪个?
生4:常量是s,变量是v和t.
师(追问):其中的变量v和t是按怎样的规律变化的?
生5:t=■或v=■.
师:在t=■中,取v=60,t值为多少?有几个值与之对应?
生6:当v=60时,t=4,有唯一的值与之对应.
师:同学们回答得都很严谨,在上述问题的讨论中,我们是否发现了常量、变量之间的什么联系?我们继续探究.
实施意图 “变量与函数”是初中学生首次接触“函数”这个抽象的概念,是进一步学习函数的基础. 本节课教学内容虽简单,但要让学生真正接受却有一定的难度,因此需要由具体的情境出发,由具体到抽象逐渐展开,引导学生主动发现知识进而掌握知识. 在本环节的最后,教师提出了问题却并没有让学生回答,显然即使不回答,学生也会在内心对这个问题进行思索,这样一方面是引导学生思考问题的方向,另一方面给学生进一步完善该问题提供机会.
小组合作,自主构建
小组合作学习是合格课堂中学生学习的主要方式,通过小组成员间的共同学习、相互促进,共同构建知识. 生生合作不仅有利于学生学习主体性的发挥,而且能够体现课堂教学的本质,即由学生主宰课堂,让学生自己学习知识.
学习任务:小组合作,完成以下问题.
(完成方式:学生独立完成后小组成员相互讨论、小组代表全班交流展示)
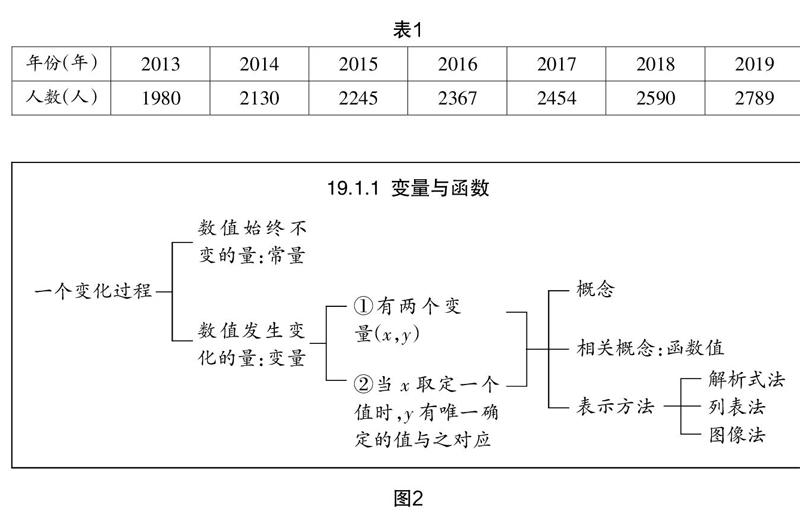
实例2 近几年某校全校学生总数统计表如表1.
(1)其中的两个量“年份”和“人数”是变量还是常量?
(2)这两个量之间有什么关系吗?
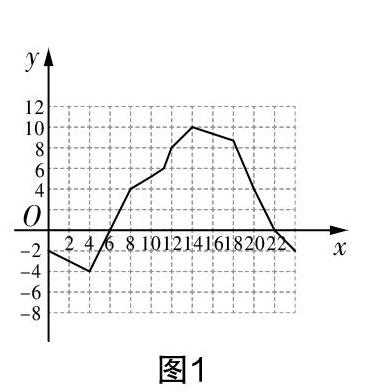
实例3 图1是我市某一天的气温T随时间t的变化而变化的图像,看图回答:
(1)0时的气温是______℃,8时的气温是______℃,24时的气温是______℃.
(2)这个气温T随着时间的变化而变化的过程中,给定时间t的值,温度是否随之确定?它所对应的值有几个?
上述问题难度较低,学生正确率高,展示部分在此不再赘述.
师:以上三个问题有什么共同点?
生1:上述三个问题都是描述一个变化过程.
生2:在上述三个问题中都有两个变量.
生3:上述问题中的两个变量,当一个变量的值确定以后,另外一个变量都有唯一确定的值与之对应.
师生共同总结函数概念:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与之对应,那么我们就说x是y的变量,y是x的函数.
函数有三种表示方法:解析式法、列表法、图像法.
实施意图 在以学生为主体的课堂中,知识应该是自然生成的,因此函数概念的学习可以交给小组合作完成. 小组合作的任务及要求明确以后学生就有了思考问题和获取新知的目标,在新知的构建中,学生彼此间会将知识逐渐完善和补充,教师不需要过分干预,这就体现了教学的本真.
任务驱动,解决问题
数学知识的学习是为了解决问题,因此用实际问题及时对所学知识进行巩固与强化是新授课的必备环节,即用所学的知识来解决例题. 在这个过程中,教师对问题的预设尤为重要,因为问题是驱动学生学习的主体,学习知识的是学生,运用知识的也是学生,只有问题具有探究价值才能体现本真教学的本质.
实例4 开学前夕,小明去文具店购买了一些练习本,单价为每本5元,买x本共用了y元.
(1)常量是______,变量是______;
(2)y与x的关系式为______;
(3)y是x的函数吗?为什么?
追问:假如买5本练习本,共需要______元,20元能买______本练习本.
变式:下列曲线中不能表示y是x的函数的是( )
实施意图 本节课以理解函数的概念及意义为目标,重点是理解,因此问题不需要太难,而需要典型,尽可能接近学生的生活,便于学生的理解与知识的迁移,所以该环节选择学生所熟知的实例进行探究. 本题是对函数概念的巩固,是基本问题,变式是在函数概念及表示的基础上进一步对函数图像特点的归纳,是由具体到抽象的过渡,具有一定的探究价值.
成果反馈,内化知识
成果反馈是新授课的最终环节,反馈的原则是先激励后矫正、先小组后全班、先过程后结论、先学生后教师. 教师在这个环节中依旧是一个组织者与引导者,在倾听学生声音后进行补充与完善,体现学生的主体性原则.
问题1:在理解函数概念时,我们要把握几个要点?
问题2:表示一个函数有哪些方法?
问题3:通过学习,你体会到函数与实际问题有什么联系?
问题4:上完这一节课,你对下节课有什么期待吗?你希望在下一节课学习哪些知识?
实施意图 本节课以概念的理解为主要教学内容,是函数的起始课,由具体到抽象理解函数的实质及意义是教学目标,因此笔者在这个环节中不再设置实际问题,而是直接让学生用语言总结本节课的内容. 问题1至问题3的设置一方面可以获知学生对概念的掌握及理解情况,以便及时对教学做出调整与优化,另外一方面让学生将所学内容通过系统的语言来表达,以此促进知识的内化. 在学生的畅所欲言中,教师完善本节课的结构式板书(见图2). 问题4是为下一节课所准备,因为课堂小结环节并非教学的终止,而是教学的再起始,引导学生对下一节课的内容形成期待,可以激发学生的学习兴趣,让学生形成自主学习的习惯.
“合格课堂”,看似朴素的四个字,其容量却是无限的. 课改是为了找到教学的本源、遵循课堂的基本原则,在这个过程中,需要教师不断学习、不断反思、不断改进,才能找回本真教学,避免教学流于形式. “授人以鱼不如授人以渔”是“教”的本真,“知其然且知其所以然”是“学”的本真,“合格课堂”正是以此为原则进行教与学的改革. 作為初中数学一线教师,笔者看到了“合格课堂+数学”的真实成效,领会到了数学的本真教学,这将促使笔者在将来的教学中不断求索、不断进步.
