修正Broer-Kaup-Kupershmidt方程的留数对称和相互作用解

史婷婷， 张顺利

(西北大学 数学学院 陕西 西安 710127)

0 引言

非线性发展方程可以用来描述等离子体物理、非线性光学、流体力学等许多物理现象。为了更好地理解这些物理现象的本质，寻找非线性发展方程的相关解就显得尤为重要。文献[1]通过Painlevé截断展开法提出了留数对称定理。同时，为了得到更多非线性系统的本质特征，文献[2]提出了一致的Riccati展开(CRE)法，在此基础上，不仅可以明确非线性系统的可积性，还可以构造孤子与其他多种非线性波之间的相互作用解[3-5]。本文主要对修正Broer-Kaup-Kupershmidt(MBKK)方程[6]

(1)

进行了研究。MBKK方程是由(2+1)维BKK方程[7]当y=x时改写得到的。BKK方程是描述非线性和色散长重力波在浅海水平方向均匀深度的模型,MBKK方程则主要用于描述浅水波的运动。目前,已有文献主要针对BKK方程进行研究,而对MBKK方程的研究较少,如文献[8]用Hirota方法把非线性方程化为双线性方程,然后通过摄动法寻找其精确解。本文首先用Painlevé分析法[9]研究MBKK方程的留数对称和相应的有限变换，其次用CRE方法得到MBKK方程的新的相互作用解。

1 MBKK方程的非局域留数对称及其局域化

由MBKK方程(1)的非线性项与色散项的平衡，可得其Painlevé截断展开[10]为

(2)

式中：u0、u1、v0、v1、φ均为x和t的函数。将方程(2)代入方程(1)，取1/φ的各次幂系数为0，可得

(3)

φ满足方程(1)的Schwartzian形式，即

2Cxx-Sx=0,

(4)

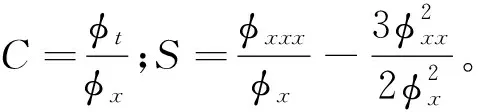
方程(4)在Möbious变化

(5)

下保持不变，这表示方程(4)拥有σφ=a、σφ=bφ和σφ=cφ2三种对称，将方程(2)代入方程(1)，可得定理1。

定理1(Bäcklund变换定理) 若φ是方程(4)的解，则

(6)

为了将留数对称局域化[11]，引入辅助变量g=g(x,t)，利用表达式

g=φx，

(7)

则方程(1)的非局域留数对称被局域化为延拓系统(1)、(6)、(7)的Lie点对称，即

(8)

相应的Lie点对称的向量场表达式为

(9)

由Lie的第一基本定理，解如下的初值问题：

(10)

可得Lie点对称(9)的有限对称变换为

(11)

式中：ε是任意群参数。

2 MBKK方程的CRE可解与新的精确解

根据CRE方法[12]，方程(1)有如下的截断展开式：

(12)

式中：ω=ω(x,t)；R(ω)是Riccati方程

Rω=l0+l1R+l2R2

(13)

的解,l0、l1、l2为任意常数,R=R(ω)。

且ω满足方程

(14)

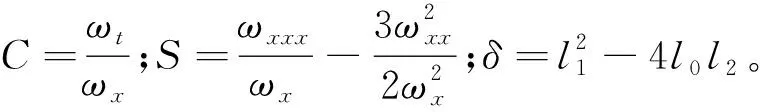
为求相互作用解，可设相容性方程(14)的解的具体形式为

ω=k1x+p1t+W(X)；X=k2x+p2t。

(15)

将式(15)代入式(14)，得到椭圆方程

(16)

式中：

(17)

其中C2,k1,k2,p2为任意常数。则MBKK方程(1)的解有如下形式：

(18)

下面通过2个例子来具体给出MBKK方程的孤立波与椭圆周期波之间的相互作用解。

例1取椭圆函数方程(16)的解为

W=cEπ(sn(k2x+p2t,m),n,m),

(19)

式中：sn(q,m)为椭圆函数；Eπ为第三类不完全椭圆积分。取l0=-1,l1=0,l2=-1,此时Riccati方程的解为R(ω)=cot(ω)。

将R(ω)=cot(ω)和式(19)代入式(18)，可得MBKK方程的相互作用解为

式中：S=sn(k2x+p2t,m)；C=cn(k2x+p2t,m)；D=dn(k2x+p2t,m)。

将式(15)和式(19)代入方程(14)，利用Maple软件解超定方程可得：c、m、k1、k2、p1、p2为任意常数，n=0。

图1为例1中u,v相互作用解的波形图,图2为x=0时u,v的平面周期波解结构。参数选择如下：{c=-0.553 931 451 6,m=0.9,n=0,k1=1,k2=1,p1=2,p2=2}。可以看出,解u,v分别具有多个不在同一平面上的波峰和波谷，且这些波峰和波谷的凹陷程度不同。

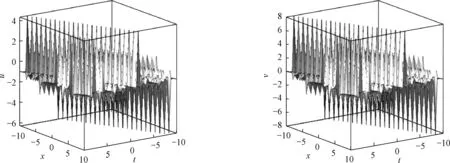
图1 例1中u,v相互作用解的波形图Figure 1 Waveform of the solutions of u and v in sample 1

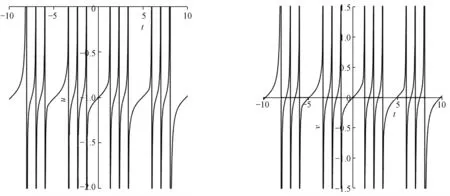
图2 例1中x=0时u,v的平面周期波解结构Figure 2 The structure of plane periodic wave solutions of uand vat x=0 in sample 1

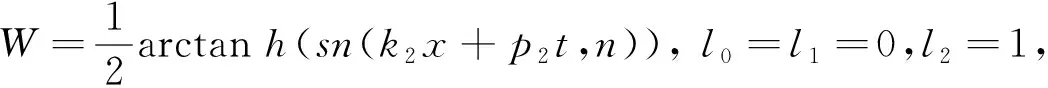
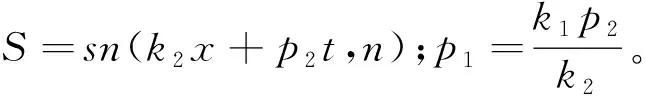
图3为例2中u,v相互作用解的波形图,图4为x=0时u,v的平面周期波解结构。参数选择如下：{n=0.568,k1=0.4,k2=0.2,p1=0.8,p2=0.4}。可以看出，解u,v分别具有多个波峰和波谷，且波峰和波谷的凹陷程度不同。

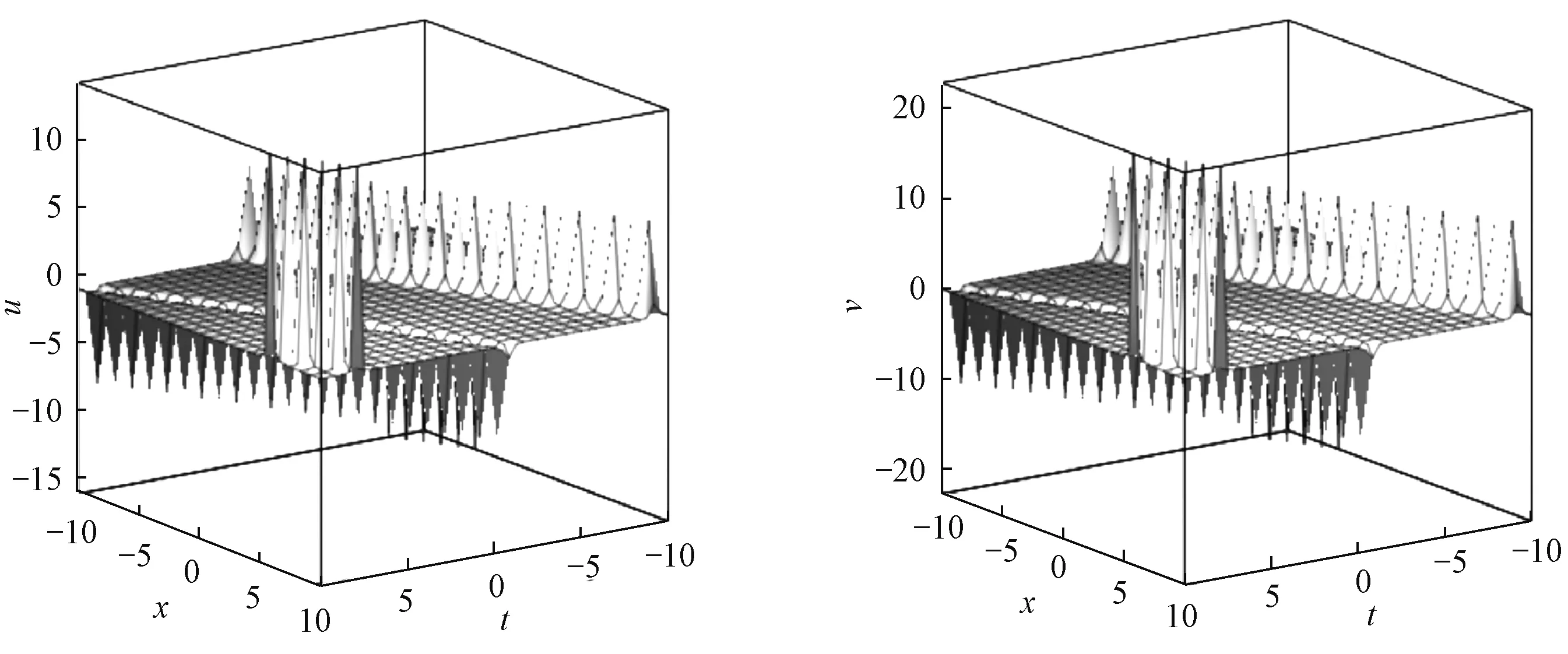
图3 例2中u,v相互作用解的波形图Figure 3 Waveform of the solutions of u and v in sample 2

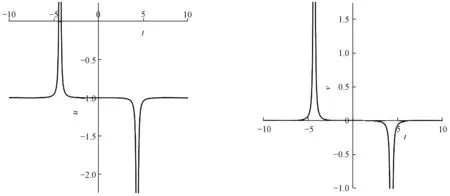
图4 例2中x=0时u,v的平面周期波解结构Figure 4 The structure of plane periodic wave solutions of u and v at x=0 in sample 2

3 结束语

由Painlevé截断展开法得到MBKK方程的留数对称,并通过引入合适的新变元将其局域化为Lie点对称,在此基础上,利用Lie的第一基本定理研究了延拓系统的有限变换。最后,用CRE方法获得了MBKK方程的相互作用解。为了更好地研究解的性质,通过选取适当的参数,给出了解的相应图形。