S3中等参曲面的两个特征

方建波,梁 林

(1.贵州财经大学数学与统计学院,贵州贵阳 550025)

(2.楚雄师范学院人事处,云南楚雄 675000)

1 引言

等参超曲面是高维微分几何中非常重要的研究对象,在三维空间称为等参曲面,这些曲面是一些平行曲面族.最简单的情况,就是一个点波源诱发的球面波,波前就是同心球面族;然后是一个线波源,诱发的同轴柱面族;或者是一个面波源诱导的平行平面族.在三维欧氏空间R3中,平行曲面之间的性质研究已出现在相关文献中,参见文献[1].在三维双曲空间H3中,平行曲面族的相关特征可参看文献[2,3].自然的想法是,在三维球空间中,平行曲面族之间又有些什么样的特征?本文将给出一个初步的探讨.

2 S3中的平行曲面的曲率

设x:M2→S3(c)为三维球空间中的曲面,ei是x的局部单位切标架,ωi为其对偶标架,e3为x的单位法向量,做M的平行曲面族{Mt}为

为方便起见,我们约束指标范围1≤i,j≤2.对于x而言,有

其中hij为M的第二基本形式的系数.对(2.1)外微分并利用(2.2)可得

即{ei}也是TxtMt的标准基,其对偶基为

而

为xt的单位法向量.一方面,

另一方面,

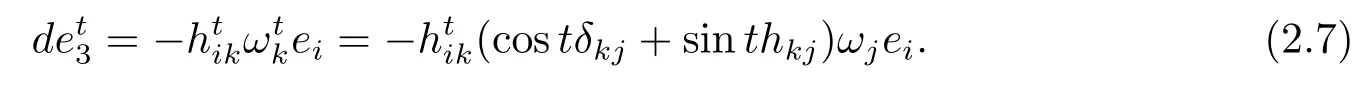
比较(2.6)和(2.7)式可得

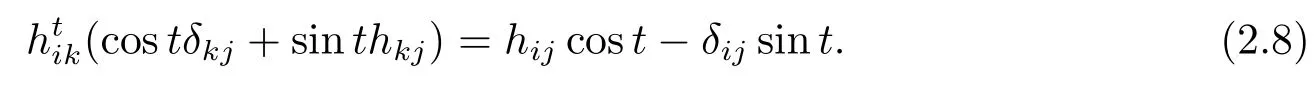
引理2.1S3中的平行曲面Mt的主曲率为

其中θi由 cotθi=λi确定.

证由(2.8)式,令hij=λiδij可得

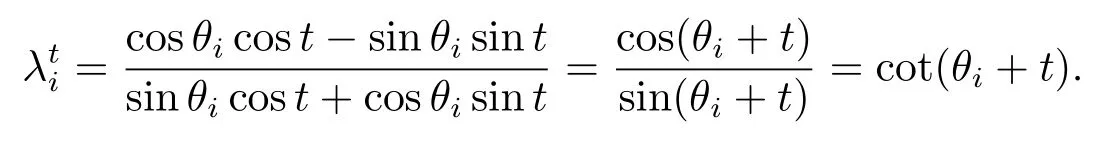
为便于主要定理的证明,我们需要下面的引理.

引理2.2设x:M2→S3(c)是三维球面上的光滑曲面,λ1,λ2是曲面上的两个主曲率,则

(1)两个主曲率λ1,λ2是曲面上的连续函数;

(2)两个主曲率λ1,λ2是曲面上在非脐点处的光滑函数.

证 现取曲面x的局部参数化(U,u,v)∈M2,x:U→S3,x=x(u,v)∈S3.它的诱导度量和第二基本形式局部上分别表示为

由于曲面的光滑性,因此度量张量的系数{g11,g12,g22}和第二基本形式的系数{h11,h12,h22}都是曲面x上关于参数u,v的光滑函数.这样矩阵

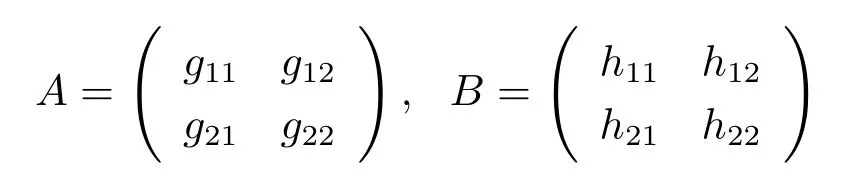
是两个光滑矩阵.既然A是正定矩阵,那么C=BA−1是一个光滑矩阵.由于曲面上的高斯曲率K和平均曲率H可以表达为这样曲面上的高斯曲率K和平均曲率H都是曲面上的光滑函数,即是参数u,v的光滑函数.

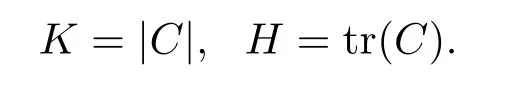
现设λ1,λ2是曲面上的两个主曲率,则λ1+λ2=2H,λ1λ2=K,从而有

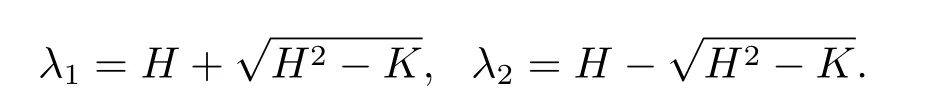
3 主要结论及证明

定理3.1M有常主曲率的充要条件是只是t的函数(k=1,2,3).

证必要性是显然的.故只需证明充分性即可,先证明结论对k=3时成立.设

对(3.1)式关于t求导,得

在(3.1)和(3.2)式中令t=0,从而得

由(3.3)和(3.5)式得

再由(3.4)和(3.6)式可得

上面的cp,p=1,2,···,6为常数.

由引理2.2知,M上的主曲率λi是局部坐标u,v的函数,因此在(3.3)和(3.4)式中分别对u,v求偏导数可得

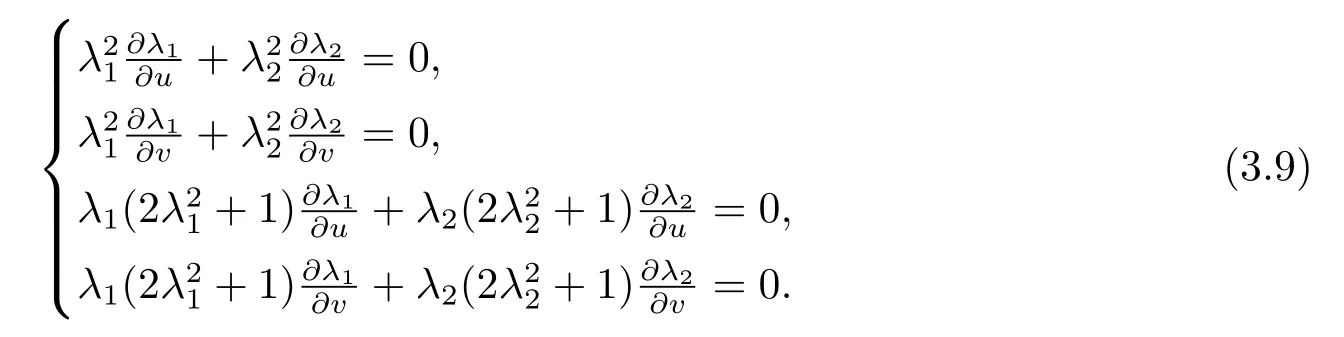
当

时,λi为常数.

同理,对(3.3)和(3.7)式做类似于(3.9)和(3.10)式的讨论可知,当

时,λi为常数.

微分(3.13)式可得方程组

下证k=2的情形.令

对(3.15)式两边关于t求二阶导数得

在(3.15)和(3.16)式中令t=0得

这里c7,c8为常数.由可知是常数,从而λ1和λ2是常数.k=1的情形类似于k=2,此处不再赘述.

定理3.2设且则M具有常主曲率的充要条件是每个Mt有常值的高斯曲率.

证必要性是显然的,下证充分性即可.令G(t)=λ1(t)λ2(t),为Mt的高斯曲率,因为λ1λ260,所以当|t|充分小时,由引理2.1可知G(t)60.作函数

上式两边对t求导得

在(3.19)和(3.20)式中令t=0得

这里c9,c10是常数,对(3.21)式做类似于(3.9)和(3.10)式的讨论可知,在的条件下,λ1,λ2是常数,证毕.