A STOCHASTIC ALTERNATING MINIMIZATION METHOD FOR SPARSE PHASE RETRIEVAL

CAI Jian-fengJIAO Yu-lingLU Xi-liangYOU Jun-tao

(1.Department of Mathematics,The Hong Kong University of Science and Technology Kowloon,Hong Kong 999077,China)

(2.School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China)

(3.School of Mathematics and Statistics;Hubei Key Laboratory of Computational Science,Wuhan University,Wuhan 430072,China)

(4.Department of Mathematics,Southern University of Science and Technology,Shenzhen 518055,China)

Abstract:Sparse phase retrieval plays an important role in many fields of applied science and thus attracts lots of attention.In this paper,we propose a stochastic alternating minimization method for sparse phase retrieval(StormSpar)algorithm which empirically is able to recover n-dimensional s-sparse signals from only O(slogn)measurements without a desired initial value required by many existing methods.In StormSpar,the hard-thresholding pursuit(HTP)algorithm is employed to solve the sparse constrained least-square sub-problems.The main competitive feature of StormSpar is that it converges globally requiring optimal order of number of samples with random initialization.Extensive numerical experiments are given to validate the proposed algorithm.

Keywords:phase retrieval;sparse signal;stochastic alternating minimization method;hard-thresholding pursuit

1 Introduction

Phase retrieval is to recover the phase information from its magnitude measurements,i.e.,

wherex∈Fnis the unknown vector,ai∈Fnare given sampling vectors which are random Gaussian vector in this paper,yiare the observed measurements,are the noise,andmis the number of measurements(or the sample size).The Fncan be Rnor Cn,and we consider the real case Fn=Rnin this work.The phase retrieval problem arises in many fields like X-ray crystallography[1],optics[2],microscopy[3]and others,see e.g.[4].Due to the lack of phase information,the phase retrieval problem is a nonlinear and ill-posed problem.

When the measurements are overcomplete,i.e.,m>n,there are many algorithms in the literature.Earlier approaches were mostly based on alternating projections,e.g.the work of Gerchberg and Saxton[5]and Fienup[4].Recently,convex relaxation methods such as phase-lift[6]and phase-cut[7]were proposed.These methods transfer the phase retrieval problem into a semi-definite programming,which can be computationally expensive.Another convex approach named phase-max which does not lift the dimension of the signal was proposed in[8].In the meanwhile,there are other works based on solving nonconvex optimization via first and second order methods including alternating minimization[9](or Fienup methods),Wirtinger flow[6]Kaczmarz[10],Riemannian optimization[11];Gauss-Newton[12,13]etc.With a good initialization obtained via spectral methods,the above mentioned methods work with theoretical guarantees.Progresses were made by replacing the desired initialization with random initialized ones in alternating minimization[14,15],gradient descent[16]and Kaczmarz method[17,18]while keeping convergence guarantee with high probability.Also,recent analysis in[19,20]showed that some nonconvex objective functions for phase retrieval have a nice landscape—there is no spurious local minima—with high probability.As a consequence,for these objective functions,any algorithms finding a local minima are guaranteed to give a successful phase retrieval.

For the large scale problem,the requirementm>nbecomes unpractical due to the huge measurement and computation cost.In many applications,the true signalxis known to be sparse.Then the sparse phase retrieval problem can be solved with a small number of samplings,thus possible to be applied to large scale problems.It was proved in[21]thatm=O(slogn/s)measurement is sufficient to ensure successful recovery in theory with high probability when the model is Gaussian(i.e.,the sampling vectoraiare i.i.d Gaussian and the target is real).But the exiting computational trackable algorithms requireO(s2logn)number of measurements to reconstruct the sparse signal,for example,‘1regularized PhaseLift method[22],sparse AltMin[9],GESPAR[23],Thresholding/projected Wirtinger flow[24,25],SPARTA[26]and so on.Two stage methods based on phase-lift and compressing has been introduced in[27,28],which is able to do successful reconstruction withO(slogn)measurements for some specially designed sampling matrix which exclude the Gaussian model(1.1).When a good initialization is available,the sample complexity can be improved toO(slogn)[25,29].However,it requiresO(s2logn)samples to get a desired sparse initialization in the existing literature.This gap naturally raises the following challenging question.

Can one recover thes-sparse target from the phaseless generic Gaussian model(1.1)withO(slogn)measurements via just using random initializations?

In this paper,we propose a novel algorithm to solve the sparse phase retrieval problems in the very limited number of measurements(numerical examples show thatm=O(slogn)can be enough).The algorithm is a stochastic version of alternating minimizing method.The idea of alternating minimization method is:during each iteration,we first given an estimation of the phase information,then substitute the approximated phase into(1.1)with the sparse constraint and solve a standard compressed sensing problem to get an updated sparse signal.But since the alternating minimization method is a local method,it is very sensitive to the initialization.Without enough measurements,it is very difficult to compute a good initial guess.To overcome this difficulty,we change the sample matrix during each iteration via bootstrap technique,see Algorithm 1 for details.The numerical experiments show that the proposed algorithm needs onlyO(slogn)measurements to recover the true signal with high probability in Gaussian model,and it works for a random initial guess.The experiments also show that the proposed algorithm is able to recover signal in a wide range of sparsity.

The rest of this paper is organized as follows.In Section 2 we introduce the setting of problem and the details of the algorithm.Numerical experiments are given in Section 3.

2 Algorithm

First,we introduce some notations. For anya,b∈Rn,we denote thatis the number of nonzero entries ofx,andis the standardl2-norm,i.e.,The floor functionis the greatest integer which is less than or equal toc.

Recall from(1.1),we denote the sampling matrix and the measurement vector by,respectively.Letx∈Rnbe the unknown sparse signal to be recovered.In the noise free case,the problem can be written as to findxsuch that

In the noisy case,this can be written by the nonconvex minimization problem

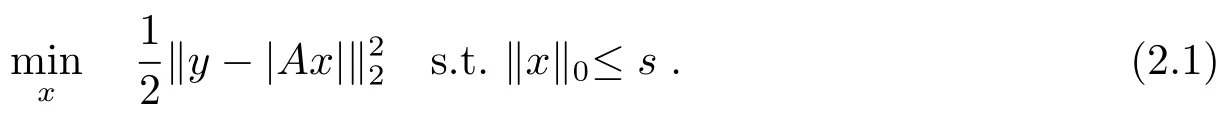
Now we propose the stochastic alternating minimization method for sparse phase retrieval(StormSpar)as follows.It starts with a random initial guessx0.In the‘-th step of iteration(=1,2,···),we first randomly choose some rows of the sampling matrixAto form a new matrixA‘(which is a submatrix ofA),and denoted by the corresponding rows ofytoThen we compute the phase information of,say,and to solve the standard compressed sensing subproblem

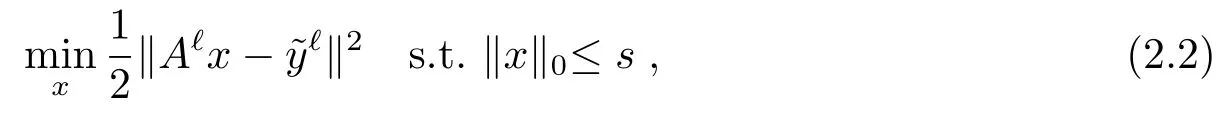
3 Numerical Results and Discussions

3.1 Implementation Details

The true signalxis chosen ass-sparse with random support and the design matrixA∈Rm×nis chosen to be random Gaussian matrix.The additive Gaussian noise following the form=σ ∗randn(n,1),thus the noise level is determined byσ.The parameterγis set to be,andδ=0.01.

The estimation errorrbetween the estimatorand the true signalxis defined as

We say it is a successful recovery when the relative estimation errorrsatisfy thatr≤1e−2 or the support is exactly recovered.The tests repeat independently for 100 times to compute a successful rate. “Aver Iter” in Tables 1 and 2 means the average number of iterations for 100 times of tests.All the computations were performed on an eight-core laptop with core i7 6700HQ@3.50 GHz and 8 GB RAM using MATLAB 2018a.

Algorithm 1 StormSpar 1:Input:Normalized A ∈ Rm×n,y,sparsity level s, γ ∈ (0,1),small constant δ,a random initial value x0.2:for ‘=1,2,···do 3:Randomly selected bγmc rows of A and y,denote the index as i‘,to form A‘=A(i‘,:)y‘=y(i‘).4:Compute p‘=sign(A‘x‘−1),˜y‘=p‘ fly‘.5:Get x‘by solving minx,kxk0≤s12kA‘x−˜y‘k2via Algorithm 2(HTP).6:Check stop criteria kx‘−x‘−1k ≤ δ.7:end for 8:Get the first s position of x‘and refit on it as output.

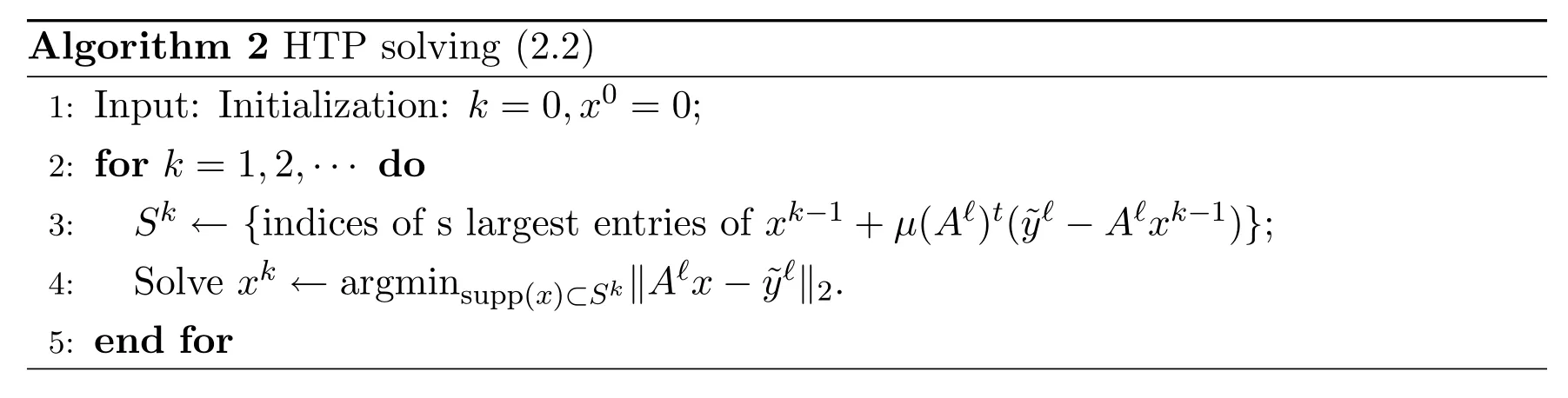
Algorithm 2 HTP solving(2.2)1:Input:Initialization:k=0,x0=0;2:for k=1,2,···do 3:Sk←{indices of s largest entries of xk−1+µ(A‘)t(˜y‘−A‘xk−1)};4:Solve xk←argminsupp(x)⊂SkkA‘x−˜y‘k2.5:end for

3.2 Examples

Example 1First we examine the effect of sample sizemto the probability of successful recovery in Algorithm 1.The dimension of the signalxisn=1000.

a)When we set sparsity to bes=10,25,50,Figure 1 shows how the successful rate changes in terms of the sample sizem.In this experiment,we fix a numberwhich is 115,287,575 with respect to the sparsity 10,25,50.Then we compute the probability of success whenm/Kchanges:for eachsand eachm/K=1,1.25,···,3,we run our algorithm for 100 times.It shows when the sample size is in orderO(slogn)in this setting,we can recover the signal with high possibility.

Figure 1 The probability of success in recovery v.s.sample size m/K for Gaussian model, which is 115,287,575 with respect to sparsity s=10,25,50,signal dimension n=1000,noise level σ=0.01

b)We compare StormSpar to some existing algorithm,i.e.,CoPRAM[31],Thresholded Wirtinger Flow(ThWF)[24]and SPArse truncated Amplitude flow(SPARTA)[26].The sparsity is set to be 30 and the model is noise free.Figure 2 shows the successful rate comparison in terms of sample size,the results are obtained by averaging the results of 100 trials.We find it that StormSpar requires more iterations and more cpu time than these algorithms which requires initialization.But StormSpar achieves better accuracy with less sample complexity.

Example 2Figure 3 shows that StormSpar is robust to noise.We setn=1000,s=20,andThe noise we added is i.i.d.Gaussian,and the noise level is shown by signal-to-noise ratios(SNR),we plot the corresponding relative error of reconstruction in the Figure 3.The results are obtained by average of 100 times trial run.

Example 3We compare StormSpar with a two-stage method Phaselift+BP proposed in[27],which has been shown to be more efficient than the standard SDP of[32].The dimension of data is set to ben=1000.The comparison are two-folder.First,for different sparsity level,we compare the minimum number of measurements required to give successful recovery rate higher than 95%,the result can be found in Figure 4.Second the average computational time is given in Figure 5,where.

Figure 2 The probability of success in recovery for different algorithms in terms of changing sample size,dimension n=1000,sparsity s=30 and the model is noise free

Figure 3 The reconstruction error v.s.SNR to measurements for Gaussian model, with sparsity s=20,signal dimension n=1000 and several noise level,i.e.SNR to measurements

Example 4Letm=O(slogn),we test for different sparse levels and different dimensions.In Table 1,we fix dimensionn=2000,and the sample size is chosen to beThe sparsity level changes from 5 to 100,we find the algorithm can successfully recover the sparse signal in most case,and the iteration number is very stable.

In Table 2,the sparsity level is fixed bys=10,the sample size isfor dimensionnfrom 100 to 10000.We find the algorithm can successfully recover the sparse signal in most cases,and the number of iteration dependent on the dimensionn.

Figure 4 Comparison of Minimum number of measurements required for Gaussian model,signal dimension n=1000 and free of noise

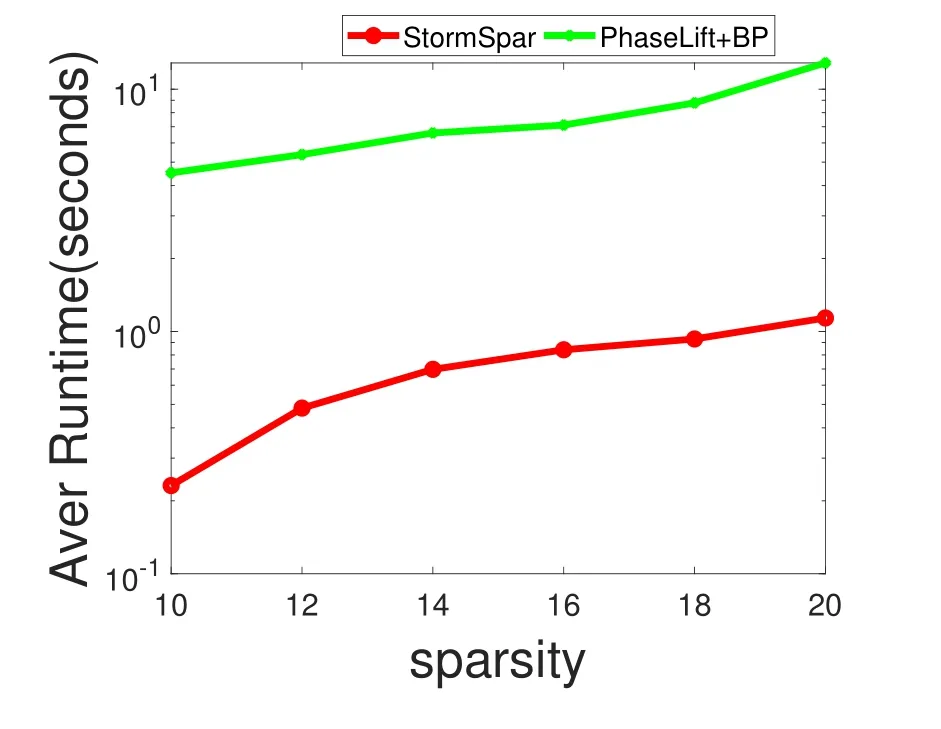
Figure 5 Comparison of efficiency for Gaussian model,signal dimension n=1000 and free of noise

4 Conclusion

In this paper,we propose a novel algorithm(StormSpar)for the sparse phase retrieval.StormSpar start with a random initialization and employ a alternating minimization method for a changing objective function.The subproblemis a standard compressed sensing problem,which can be solved by HTP method.Numerical examples show that the proposed algorithm requires onlyO(slogn)samples to recover thes-sparse signal with a random initial guess.

Table 1 Numerical results for sparsity test,with random sampling A of size n×m,n=2000,s is the sparsity,with σ=0.01,and Aver Iter= average number of iterations for 100 times of test

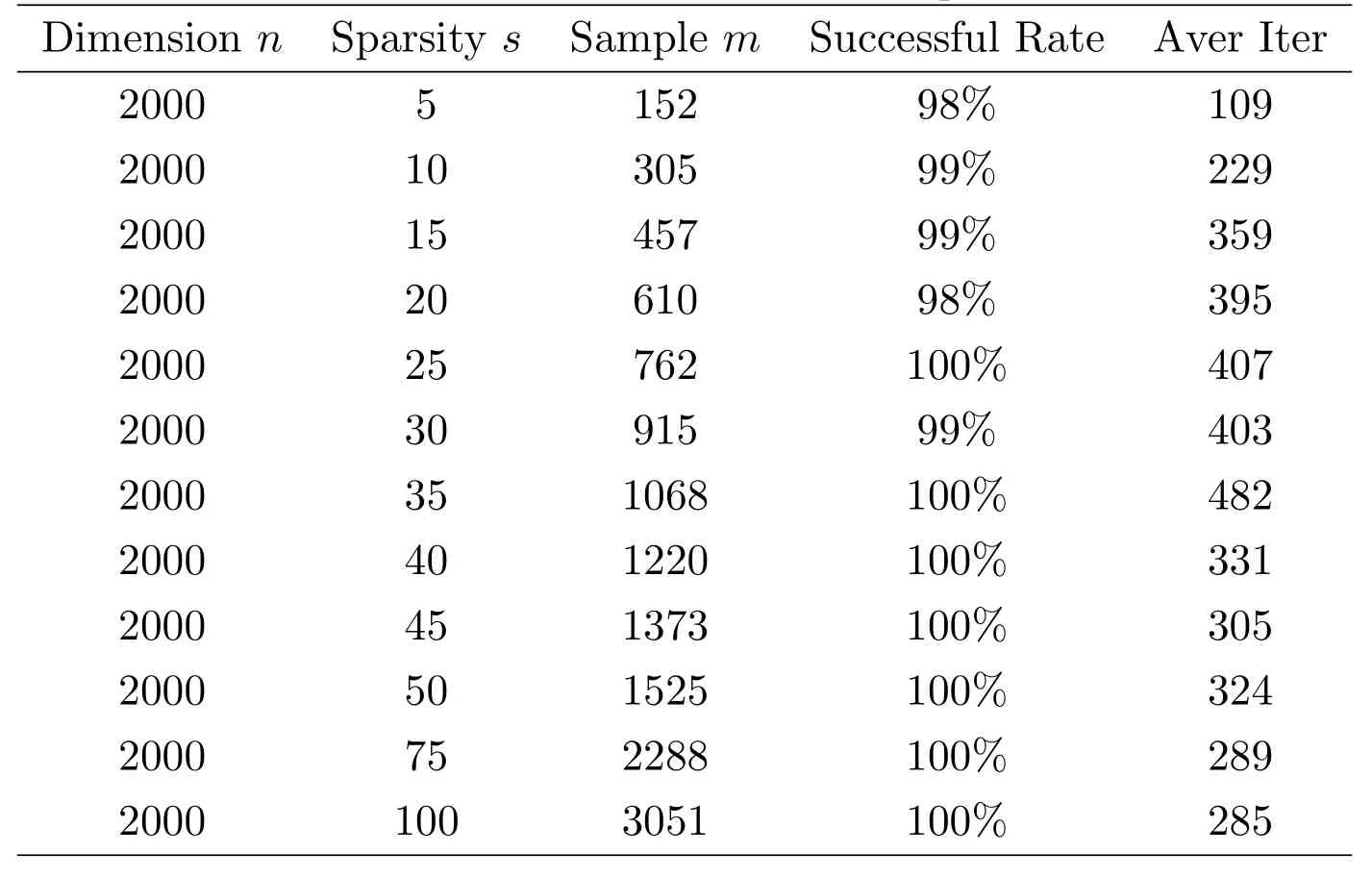
Table 1 Numerical results for sparsity test,with random sampling A of size n×m,n=2000,s is the sparsity,with σ=0.01,and Aver Iter= average number of iterations for 100 times of test

Dimension n Sparsity s Sample m Successful Rate Aver Iter 2000 5 152 98% 109 2000 10 305 99% 229 2000 15 457 99% 359 2000 20 610 98% 395 2000 25 762 100% 407 2000 30 915 99% 403 2000 35 1068 100% 482 2000 40 1220 100% 331 2000 45 1373 100% 305 2000 50 1525 100% 324 2000 75 2288 100% 289 2000 100 3051 100% 285

Table 2 Numerical results for different dimensions,with random sampling A of size s is the sparsity,with σ=0.01,and Aver Iter=average number of iterations for 100 times of test

Table 2 Numerical results for different dimensions,with random sampling A of size s is the sparsity,with σ=0.01,and Aver Iter=average number of iterations for 100 times of test

Dimension n Sparsity s Sample m Successful Rate Aver Iter 100 10 230 98% 38 200 10 249 99% 46 300 10 257 100% 56 400 10 264 100% 72 500 10 270 100% 93 750 10 280 100% 123 1000 10 287 100% 157 1500 10 297 99% 192 2000 10 305 99% 229 3000 10 315 99% 298 4000 10 322 98% 508 5000 10 328 97% 748 7500 10 338 95% 1142 10000 10 345 96% 1271