半素环上的左理想①

刘双双

(吉林师范大学研究生院，吉林 长春130000)

0 引 言

本文中，R 是结合环，I 是R 的左理想，d 是R 的导子，F 是R 的广义导子.Daif 和Bell［1］证明了若R是带有非零左理想I 的半素环，d 是R 的导子，使得d(［x，y］)=±［x，y］，x，y ∈I，，则R 是可交换的.最近，Quadri et al.［2］已经将这一结果推广到素环的广义导子上.

Basudeb Dhara［3］又在半素环的情况下研究了［2］的结果.本文中，我们将在半素环的左理想上讨论相似的恒等式.

1 主要结果

定理1 R 是2－扭自由半素环，I 是R 的非零左理想.d:R →R 是R 的非零导子，F:R →R 是R 的广义导子.若F(u)u=ud(u)，u ∈I，则［I，I］d(I)=0.

证明: 由假设知，

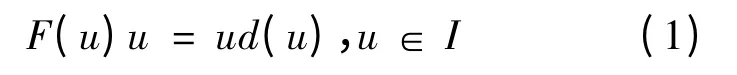
在(1)中令u=u+v，得到

在(2)中令v=vu，得到

在(3)中令v=ωv，得到［u，ω］vd(u)=0 u，v，ω ∈I

由于I 是非零左理想，则有［u，ω］Rvd(u)=0 u，v，ω ∈I.由于R 是半素环，它必包含一个素理想的集族Ω={Pα|α ∈Λ}，使得∩α∈ΛPα={0}［4］.若P 是Ω 的典型元，x ∈I，则有［x.I］⊆P 或Id(x)⊆P.对于给定P，集合T1={x ∈I|［x，I］⊆P}与T2={x ∈I|Id(x)⊆P}是I 的两个可加真子群，则I=T1∪T2.因此I=T1或I=T2，即［I，I］⊆P 或Id(I)⊆P，则有［I，I］d(I)⊆P，∀P ∈Ω，.于是［I，I］d(I)⊆∩α∈ΛPα=0.

定理2 R 是2－扭自由半素环，I 是R 的非零左理想.d:R →R 是R 的非零导子，F:R →R 是R 的广义导子.若d(u2)=2F(u)u，u ∈I，则［I，I］d(I)=0.

证明: 有假设知d(u2)=2F(u)u，u ∈I，即，

由上式的线性变换得到

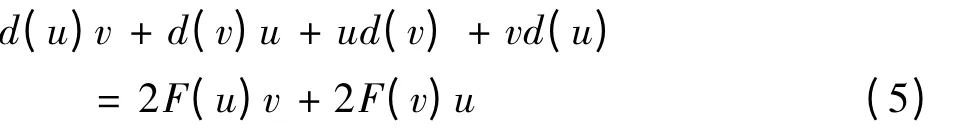
在上式中令v=vu，得到

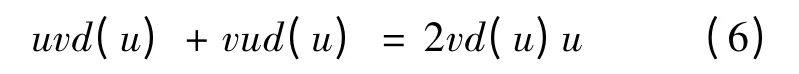
即，

在(7)中令v=ωv，得到［u，ω］vd(u)=0，u，v，ω ∈I.因此有［u，ω］Rvd(u)=0.接下来的讨论过程与定理1 相同，即可得到［I，I］d(I)=0.

定理3 R 是2－扭自由半素环，I 是R 的非零左理想.d:R →R 是R 的非零导子，F:R →R 是R 的广义导子.若［F(u)，u］=0，u ∈I，，则［I，I］d(I)=0.

证明: 有假设知，

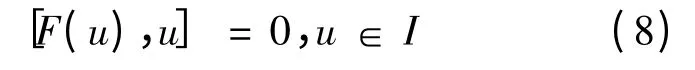
由上式的线性变化得到

在上式中令v=vu，得到

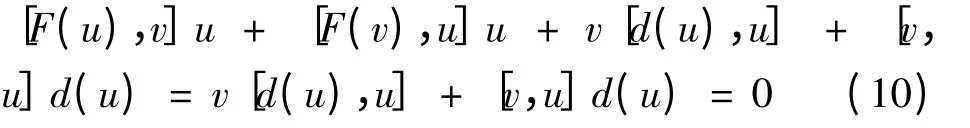
在(10)中令v = ωv，得到［ω，u］vd(u)=0 u，v，ω ∈I，因此有［u，ω］Rvd(u)=0.接下来的讨论过程与定理1 相同，即可得到［I，I］d(I)=0.

［1］ M.N.Daif and H.E.Bell.Remark on Derivations on Semiprime Ring［J］.International Journal of Mathematics and Mathematical Sciences，vol.15，no.1，pp.205－206，1992.

［2］ M.A.Quadri，M.S.Khan，and N.Rehman.Generalized Derivations and Commutativity of Prime Ring，Indain［J］.Journal of Pure and Applied Mathematics，vol.34，no.9，pp.1393－1396，2003.

［3］ B.Dhara.Remark on Generalized Derivations in Prime and Semiprime Rings［J］.International Journal of Mathematics and Mathematical Sciences，vol.2010，Article ID 646587，6 pages，2010.

［4］ Basudeb Dhara and Atanu Pattanayak.Generalized Derivations and Left Ideals in Prime and Semiprime Rings［M］.Interinational Scholarly Research Network ISRN Algebra Volume 2011，ARticle ID 750382，5 pages doi:10.5402 /2011/750382.