K1，5，p和 K1，6，p的点可区别的IE-全染色及一般全染色

寇艳芳 ，陈祥恩 ，王治文

(1. 西北师范大学 数学与统计学院, 甘肃 兰州 730070； 2. 宁夏大学 数学与统计学院, 宁夏 银川 750021)

0 引 言

点可区别一般边染色由HARARY等[1]于1985年提出，在文献[1-6]中均有涉及．

近年来，点可区别的未必正常的全染色也得以研究.CHEN等[7]提出了点可区别IE-全染色，而LIU等[8]提出了一般点可区别全染色．

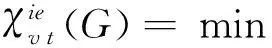
本文研究K1，5，p和K1，6，p的点可区别IE-全染色和一般点可区别全染色，并给出了其点可区别IE-全色数和一般点可区别全色数.其完全三部图Km，n，p的顶点集合为V=X∪Y∪Z,其中，X={x1,x2,…,xm},Y={y1,y2,…,yn},Z={z1,z2,…,zp},边集合为{xiyj|i=1，2,…,m;j=1，2,…,n}∪{yjzt|j=1，2,…,n;t=1，2,…,p}∪{xizt|i=1，2,…,m;t=1，2,…,p},当m=1时，记X={x}．

约定文中图的l-VDIETC或l-GVDTC所使用的l种颜色为1，2,…,l，令Al={1，2,…,l}．

1 准备工作

一个图的点可区别IE-全染色一定是点可区别一般全染色，因此下述命题成立．

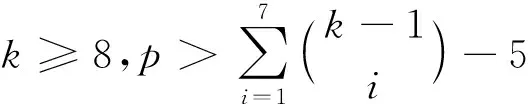
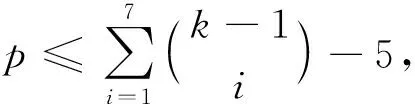
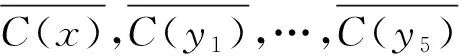
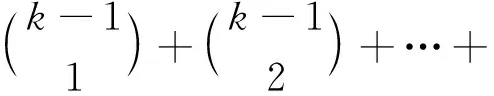
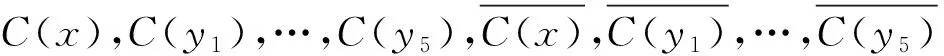
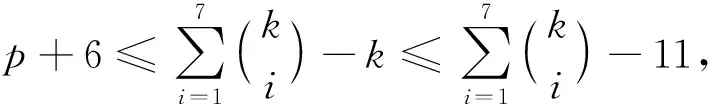
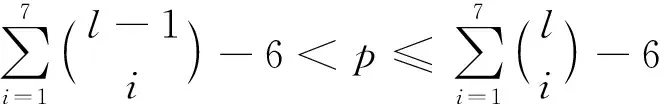
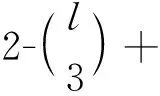
下面给出K1，5，p的一个l-IE-全染色f.令f(x)=1,f(yj)=2,j=1，2,…，5;用maxD(zi)染点zi，i=1，2,…,p.而zi的关联边均染以i+5,i=1，2,…,l-5.对|D(zi)|=2,用min[D(x)∩D(zi)]染边xzi，min[D(yj)∩D(zi)]染边yjzi,j=1，2,…，5;对|D(zi)|=3,用min[D(x)∩D(zi)]染边xzi,min[(D(yj)∩D(zi)){f(xzi)}]染边yjzi,j=1，2,…，5;对|D(zi)|=4,用min[D(x)∩D(zi)]染边xzi,min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,min[(D(yj))∩D(zi){f(xzi),f(y1zi)}]染边yjzi,j=2,3,4，5;对|D(zi)|=s(5≤s≤7),用min[D(x)∩D(zi)]染边xzi,min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,…,min[(D(yj)∩D(zi)){f(xzi),f(y1zi),…,f(yj-1zi)}]染边yjzi,j=2,3,…,s-2;min[D(yj)∩D(zi)]染边yjzi,j=s-1,s,…，5;min[D(x)∩D(yj)]染边xyj,j=1,2,…，5．

最后得到K1，5，p的l-IE全染色f是点可区别的，因为对∀v∈V(K1，5，p),均有C(v)=D(v)．

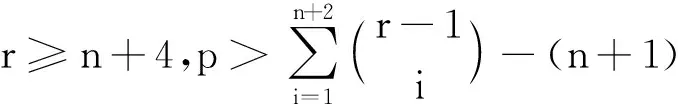
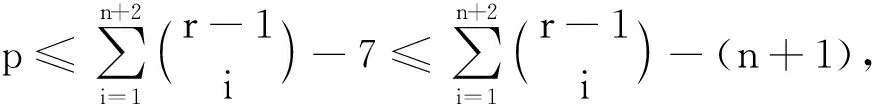
假设{3},{4},…,{r-1}均为Z中点的色集合，那么{2，3,…,r-1}⊆C(yj),j=1，2,…,n,矛盾．不妨设{3}为非Z中任意点的色集合，当n=5时，有以下2种情况:

(i) {4},{5},…,{r-1}中有一个非Z中任意点的色集合.不妨设{4}为非Z中任意点的色集合，这样{1},{2},{1，2},{3},{4}均非Z中点的色集合,那么除这5个子集外，Ar-1的其他1-子集，2-子集，…，7-子集均为Z中点的色集合，特别地，单元集{5}，{6}，…，{r-1}及{1，3}，{1，4}，{2，3}，{2，4}，{3，4}均为Z中点的色集合.那么{2，5，6,…,k-1}⊆C(yj)(j=1，2,…，5),且C(yj)含1，3，4中的至少某2种色.故每个C(yj)是Ar-1,Ar-1{1},Ar-1{3},Ar-1{4}之一，矛盾．

(ii) {4},{5},…,{r-1}均为Z中点的色集合.则{1，4,…,r-1}⊆C(x)，{2，4,…,r-1}⊆C(yj)(j=1，2,…，5),这样每个C(yj)为Ar-1，Ar-1{1}，Ar-1{3},Ar-1{1，3}之一,矛盾．

当n=6时，有以下3种情况:

(i) 当{4},{5},…,{r-1}均为Z中点的色集时,同上可推出矛盾．

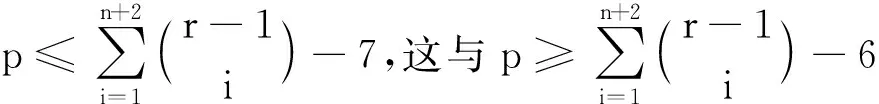
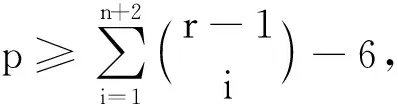
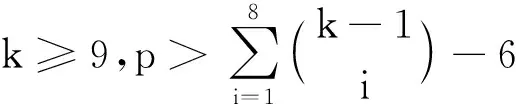
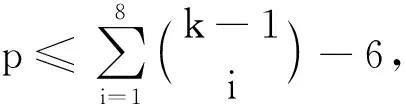
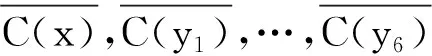
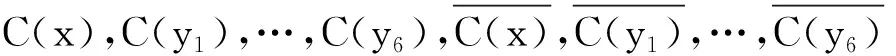
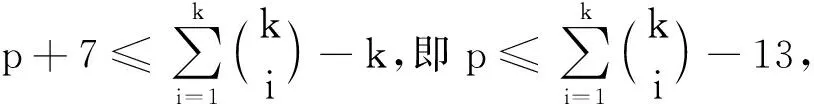
下设k=5,在K1，6，19的5-GVDTC下，{1，2，3，4，5}的所有2-子集，3-子集，4-子集，5-子集恰好构成K1，6，19的全体顶点的色集合.每个2-子集及其补集不属于不同部的2个顶点的色集合，每个2-子集及其补集只能同时是Y中点的色集合或同时都是Z中点的色集合.当然有某个2-子集是Z中点的色集合.不妨设{1，2}∈{C(z)|z∈Z},那么{3，4},{3，5},{4，5}∈{C(z)|z∈Z}，进而{1，5},{2，5},{1，4},{2，4},{1，3},{2，3}∈{C(z)|z∈Z},从而10个2-子集及其补集都必须是Z中点的色集合，但Z中仅有19个顶点，矛盾．

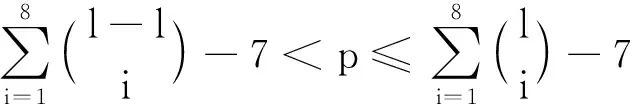
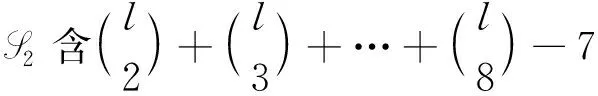
下面给出K1，6，p的一个l-IE-全染色f.令f(x)=1,f(yj)=2,j=1，2,…，6;用maxD(zi)染点zi，i=1，2,…,p.而zi的关联边均染以i+6,i=1，2,…,l-6.对|D(zi)|=2,用min[D(x)∩D(zi)]染边xzi，min[D(yj)∩D(zi)]染边yjzi,j=1，2,…，6;对|D(zi)|=3,用min[D(x)∩D(zi)]染边xzi,min[(D(yj)∩D(zi)){f(xzi)}]染边yjzi,j=1，2,…，6;对|D(zi)|=4,用min[D(x)∩D(zi)]染边xzi,min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,min[(D(yj)∩D(zi)){f(xzi),f(y1zi)}]染边yjzi,j=2,3,…，6;对|D(zi)|=s′(5≤s′≤8),用min[D(x)∩D(zi)]染边xzi,min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,…,min[(D(yj)∩D(zi)){f(xzi),f(y1zi),…,f(yj-1zi)}]染边yjzi,j=2,3,…,s′-2;min[D(yj)∩D(zi)]染边yjzi,j=s′-1,s′,…，6;min[D(x)∩D(yj)]染边xyj,j=1,2,…，6．

最后得到K1，6，p的l-IE全染色f是点可区别的，因为对∀v∈V(K1，6，p),均有C(v)=D(v)．

2 主要结果及其证明

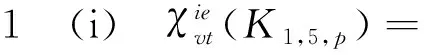
(ii)χgvt(K1，5，p)=

证明分以下几种情形进行讨论:

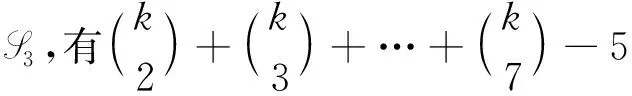
下面给出K1，5，p的k-GVDTCf.令f(x)=f(yj)=k,j=1，2,…，5;用maxD(zi)染点zi，i=1，2,…,p.而zi的关联边均染以i+5,i=1，2,…,k-5.对|D(zi)|=2,用min[D(x)∩D(zi)]染边xzi，min[D(yj)∩D(zi)]染边yjzi,j=1，2,…，5;对|D(zi)|=3,用min[D(x)∩D(zi)]染边xzi,用min[(D(yj)∩D(zi)){f(xzi)}]染边yjzi,j=1，2,…，5;对|D(zi)|=4,用min[D(x)∩D(zi)]染边xzi,用min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,用min[(D(yj)∩D(zi)){f(xzi),f(y1zi)}]染边yjzi,j=2,3,…，5;对|D(zi)|=q(5≤q≤7),用min[D(x)∩D(zi)]染边xzi,用min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,…,用min[(D(yj)∩D(zi)){f(xzi),f(y1zi),…,f(yj-1zi)}]染边yjzi,j=2,3,…,q-2;用min[D(yj)∩D(zi)]染边yjzi,j=q-1,q,…，5;用min[D(x)∩D(yj)]染边xyj,j=1,2,…，5．

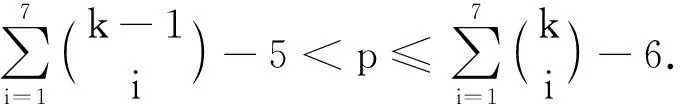
情形3当p=496时，在引理1(i)中令k=9,得K1，5，496无8-GVDTC.而K1，5，496的10-VDIETC可由引理2中的染色规则得到．

同时K1，5，495的9-VDIETC的构造类似于引理2，不再详述．

情形5K1，5，244无8-VDIETC.只要在引理3的证明过程中令r=9便可得.但其有9-VDIETC(可由K1，5，494的9-VDIETC限制在{x,y1,…,y5,z1,…,z244}上得到).同时,在引理1(i)中令k=8，可知K1，5，244无7-GVDTC,其8-GVDTC可依照情形1构造．

情形6117≤p≤243.先证K1，5，p无7-GVDTC.在引理1(ii)中令k=7,可知K1，5，117无7-GVDTC．但K1，5，p有8-VDIETC,K1，5，243的8-VDIETC的构造类似于引理2．

情形7K1，5，116无7-VDIETC.只要在引理3的证明过程中令r=8便可得.但它有8-VDIETC，可通过将K1，5，243的8-VDIETC限制在{x,y1,…,y5,z1,…,z116}上得到.同时，在引理1(ii)中令k=6，可知K1，5，116无6-GVDTC.而7-GVDTC可依照情形1构造．

情形853≤p≤115.先证K1，5，p无6-GVDTC.在引理1(ii)中令k=6,可知K1，5，53无6-GVDTC．但K1，5，p有7-VDIETC,K1，5，115的7-VDIETC的构造类似于引理2．

情形9K1，5，52无6-VDIETC.只要在引理3的证明过程中令r=7便可得.但其有7-VDIETC，可通过将K1，5，115的7-VDIETC限制在{x,y1,…,y5,z1,…,z52}上得到.同时，在引理1(ii)中令k=5，可知K1，5，52无5-GVDTC,有6-GVDTC,可依照情形1构造．

情形1021≤p≤51.先证K1，5，p无5-GVDTC.在引理1(ii)中令k=5,可知K1，5，21无5-GVDTC．但K1，5，p有6-VDIETC,K1，5，51的6-VDIETC构造类似于引理2．

情形11K1，5，20无5-VDIETC.只要在引理3的证明过程中令r=7便可得.但其有6-VDIETC，可通过将K1，5，51的6-VDIETC限制在{x,y1,…,y5,z1,…,z20}上得到.同时，K1，5，20无4-GVDTC(否则，{1，2，3，4}的非空子集不能区分诸顶点)，但有5-GVDTC,可依照情形1构造．

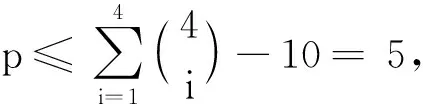
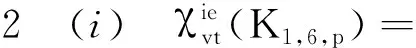
(ii)χgvt(K1，6，p)=

证明分以下几种情形讨论:

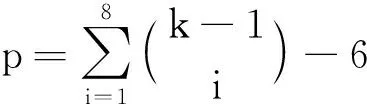
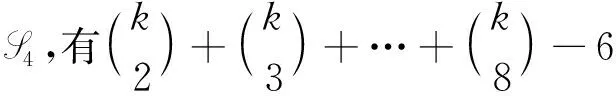
下面给出K1，6，p的k-GVDTCf.令f(x)=f(yj)=k,j=1，2,…，6;用maxD(zi)染点zi，i=1，2,…,p.而zi的关联边均染以i+6,i=1，2,…,k-6.对|D(zi)|=2,用min[D(x)∩D(zi)]染边xzi，用min[D(yj)∩D(zi)]染边yjzi,j=1，2,…，6;对|D(zi)|=3,用min[D(x)∩D(zi)]染边xzi，min[(D(yj)∩D(zi)){f(xzi)}]染边yjzi,j=1，2,…，6;对|D(zi)|=4,用min[D(x)∩D(zi)]染边xzi，用min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,用min[(D(yj)∩D(zi)){f(xzi),f(y1zi)}]染边yjzi,j=2,3，…，6;对|D(zi)|=q′(5≤q′≤8),用min[D(x)∩D(zi)]染边xzi,用min[(D(y1)∩D(zi)){f(xzi)}]染边y1zi,…，用min[(D(yj)∩D(zi)){f(xzi),f(y1zi),…,f(yj-1zi)}]染边yjzi,j=2,3，…,q′-2;用min[D(yj)∩D(zi)]染边yjzi,j=q′-1,q,…，6;用min[D(x)∩D(yj)]染边xyj,j=1,2,…，6．

情形2当p=1 006时，在引理4(i)中令k=10,得K1，6，504无9-GVDTC,那么K1，6，1 006无9-GVDTC．

而K1，6，p有10-VDIETC,其染色类似于引理5，不再赘述．

情形4K1，6，498无9-VDIETC.只要在引理3的证明过程中令r=10便可得.但其有10-VDIETC,可通过将K1，6，1 005的10-VDIETC限制在{x,y1,…,y6,z1,…,z498}上得到.同时，在引理4(ii)中令k=8，可知K1，6，498无8-GVDTC,有9-GVDTC,可依照情形1构造．

情形5当243≤p≤497时，先证K1，6，p无8-GVDTC.在引理4(ii)中令k=8，可知K1，5，243无8-GVDTC.但K1，6，p有9-VDIETC,K1，6，497的9-VDIETC构造类似于引理5．

情形6K1，6，242无8-VDIETC.只要在引理3的证明过程中令r=9则可得.但其有9-VDIETC，可通过将K1，6，497的9-VDIETC限制在{x,y1,…,y6,z1,…,z242}上得到.同时，在引理4(ii)中令k=7，可知K1，6，242无7-GVDTC,有8-GVDTC,可依照情形1构造．

情形7当115≤p≤241时，先证K1，6，p无7-GVDTC.在引理4(ii)中令k=7，可知K1，6，115无7-GVDTC.但K1，6，p有8-VDIETC,K1，6，241的8-VDIETC构造类似于引理5．

情形8K1，6，114无7-VDIETC.只要在引理3的证明过程中令r=8便可得.但其有8-VDIETC，可通过将K1，6，241的8-VDIETC限制在{x,y1,…,y6,z1,…,z114}上得到.同时，在引理4(ii)中令k=6，可知K1，6，114无6-GVDTC,有7-GVDTC,可依照情形1构造．

情形9当51≤p≤113时，在引理4(ii)中令k=6,可知K1，6，51无6-GVDTC.但K1，6，p有7-VDIETC，K1，6，113的7-VDIETC构造类似于引理5．

情形10K1，6，50无6-VDIETC.只要在引理3的证明过程中令r=7便可得.但其有7-VDIETC，可通过将K1，6，113的7-VDIETC限制在{x,y1,…,y6,z1,…,z50}上得到.同时，在引理4(ii)中令k=5，可知K1，6，50无5-GVDTC,有6-GVDTC,可依照情形1构造．

情形11当19≤p≤49时，在引理4(ii)中令k=5,可知K1，6，19无5-GVDTC.但K1，6，p有6-VDIETC，K1，6，49的6-VDIETC构造类似于引理5．

情形12当p=18时，K1，6，18无5-VDIETC.只要在引理3的证明过程中令r=6便可得.但其有6-VDIETC，可通过将K1，6，49的6-VDIETC限制在{x,y1,…,y6,z1,…,z18}上得到.同时易证K1，6，18无4-GVDTC，而有5-GVDTC.将{1，2，…，5}的所有5-子集，4-子集，3-子集，2-子集依次分配给X，Y，Z中点的色集合，可得其染色(25-1-5>p+7)．

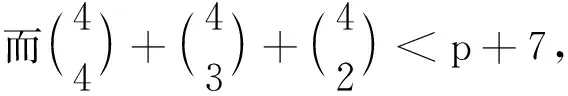
对于一般的完全三部图的VDIETC与GVDTC，笔者正在进一步探索中．