正合范畴的整体Gorenstein维数

郭景阁,王君甫,赵仁育

(1.西北师范大学数学与统计学院,甘肃 兰州 730070)

(2.常州工学院理学院,江苏 常州 213032)

0 引言

1995年,Enochs和Jenda在文献[1]中引入了Gorenstein内射模和Gorenstein投射模的概念.自此,Gorenstein同调代数逐渐被人们所关注,至今已发展成一个比较完整的理论体系.2010年,Bennis和Nahdou在文献[2]中证明了sup{GpdRM|M是左R-模}=sup{GidRM|M是左R-模},并把这个值定义为环R的左整体Gorenstein维数.2004年,Holm在文献[3]中证明了对左R-模M,N,如果GpdRM<∞,GidRN<∞,那么对任意的i≥0,并由此定义了Gorenstein导出函子在文献[4,5]中Asadollahi和Salarian研究了三角范畴中的Gorenstein同调理论.2014年,Ren和Liu在文献[6]中研究了三角范畴的整体Gorenstein维数和三角范畴中的Gorenstein导出函子.2015年,Wang在文献[7]中研究了正合范畴中的Gorenstein投射性和Tate上同调.

受以上工作启发,本文研究正合范畴的整体Gorenstein维数和正合范畴中的Gorenstein导出函子.全文分为三个部分:第一部分介绍一些相关的概念及事实;第二部分证明了在有足够多投射对象,足够多内射对象,有可数直和及可数直积的正合范畴A中,sup{GpdM|M∈A}=sup{GidM|M∈A},由此将这个值定义为A的整体Gorenstein维数;第三部分,证明在有足够多投射对象和足够多内射对象的正合范畴A中,对任意的M,N∈A,如果GpdM<∞,GidN<∞,那么由此把这个同构意义下唯一的Abel群定义为A中对象M,N确定的Gorenstein上同调群.

1 预备知识

设A是一个加法范畴,A中的核-余核对(i,p)是可合成的态射使得i是p的核,p是i的余核.令是A中一些核-余核对构成的类.称A中的态射i是可许单的,如果存在态射p,使得(i,p);称A中的态射p是可许满的,如果存在态射i,使得(i,p).用表示可许单态射,表示可许满态射.

定义1.1[8]设A是加法范畴,是A中一些核-余核对构成的类,且关于同构封闭.称是A上的正合结构,如果

称加法范畴A和其上的正合结构构成的二元组()为正合范畴,中的元素称为可许对或短正合序列.以下将正合范畴()简记为A.

称A中的态射f:A→B是可许的,如果存在可许单态射m和可许满态射e,使得下图可交换

称可许态射的序列

设P∈A,称P是正合范畴A中的投射对象,如果对A中的任意短正合序列ABC,Abel群的序列

正合.用P表示A中所有投射对象的类.称正合范畴A有足够多的投射对象,如果对任意的M∈A,存在一个投射对象P和可许满态射PM.

设A是正合范畴,M∈A.对象M的投射分解是正合序列···→Pn→···→P1→P0M,其中对任意的i≥0,Pi∈P,P0M是一个可许满态射.设M∈A,用pdM表示M的投射维数,定义为:当M=0时,pdM=−1;当M∈P时,pdM=0;设n是一个正整数,若存在短正合序列KPM,使得P∈P,pdK≤n−1,则pdM≤n.用表示A中所有投射维数有限的对象构成的类.

对偶地,可以定义A中的内射对象,A中对象的内射分解以及内射维数.用I表示A中所有内射对象构成的类,用表示A中所有内射维数有限的对象构成的类.

以下总假定A是有足够多投射对象和足够多内射对象的正合范畴.此时,由文献[8,注12.11],对任意的n≥0及任意的M,N∈A,Ext群其中PM是M的一个投射分解,N‰I是N的一个内射分解.

命题1.2设M是A中的对象,n≥0,则以下等价

(1)pdM≤n.

(2)对任意的N∈A和任意的i>n,.

(3)对任意的N∈A,.

(4)对A中的任意正合序列Kn‰Pn−1→···→P0‡M,如果P0,...,Pn−1∈P,那么Kn∈P.

证(2)⇒(3)显然.

(1)⇒(2)因为 pdM≤n,所以存在M的投射分解

因为对任意的i>n,Pi=0,所以.

(3)⇒(4)设是A中的正合序列,其中P0,···,Pn−1∈P.从而对任意的N∈A,由及(3)知所以Kn是投射的.

(4)⇒(1)设是M∈A的一个投射分解,则有正合列由(4)知Kn∈P,所以pdM≤n.

对A中对象的内射维数有对偶的结论.

2 正合范畴的整体Gorenstein维数

定义2.1[7]称A中的短正合序列ABC是HomA(−,P)-正合的,如果对任意的Q∈P,Abel群的序列

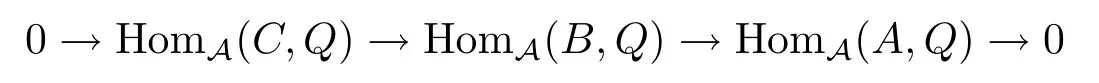
正合.

定义2.2[7]称正合序列是完全投射分解,如果对任意的n∈Z,Pn∈P,且短正合序列是HomA(−,P)-正合的.此时,称Kn是A中的Gorenstein投射对象.用GP表示A中所有Gorenstein投射对象的类.

对偶地可以定义A中的完全内射分解和Gorenstein内射对象.用GI表示A中所有Gorenstein内射对象的类.

定义2.3[7]设M∈A,用GpdM表示M的Gorenstein投射维数,定义为:若M=0,则GpdM=−1;若M∈GP,则GpdM=0;如果存在一个短正合序列KGM,其中G∈GP,GpdK≤n−1,那么 GpdM≤n.如果对任意的n≥0,Gpd,那么令GpdM=∞.用表示A中所有Gorenstein投射维数有限的对象构成的类.

对偶地可以定义A中对象的Gorenstein内射维数GidM.用fGI表示A中所有Gorenstein内射维数有限的对象构成的类.

命题2.4设A是正合范畴.若A有可数直和,则GP关于可数直和与直和项封闭.

证设{Mi}i∈Z是A中的一簇对象,且对任意的i∈Z,Mi∈GP,下证⊕i∈ZMi∈GP.因为Mi∈GP,所以存在完全投射分解

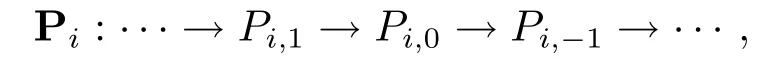
使得对任意的n∈Z,存在短正合序列Ki,nPi,n−1Ki,n−1,其中Mi=Ki,0.则由文献[8,命题2.9]知有正合列

由文献 [9,P433]知,对任意的正合,所以⊕i∈ZPi是完全投射分解,故⊕i∈ZMi∈GP.

下证GP关于直和项封闭.设M∈GP，且M=M0⊕M00.令N=M⊕M⊕···.则N=M0⊕M00⊕M0⊕M00⊕···,故N.由文献 [8,引理2.7]知M0M0⊕NN是短正合序列.因为GP关于直和封闭,所以由文献[7,引理2.2,定理2.4]和文献[10,命题1.4]知GP关于直和项封闭.

命题2.5设A是正合范畴.若A有可数直和,则对A中任何一簇对象{Mi}i∈Z,

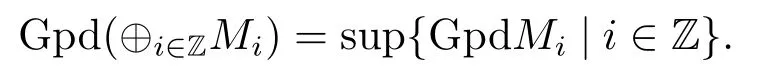
证因为GP关于可数直和封闭,所以≤成立.设M∈A,下面证明如果M0是M的直和项,那么GpdM0≤GpdM即可.

设GpdM=n<∞,对n进行归纳.当n=0时,由命题2.4知M0∈GP,所以GpdM0=GpdM.设n>0,且假定结论对n−1的情形成立.设M=M0⊕M00,取短正合序列K0G0M0与K00G00M00,其中G0,G00∈P.则由文献[8,定理12.8]有如下行、列正合的交换图

由文献[8,推论11.6]和文献[7,引理2.2]知G0⊕G00∈GP.因为GpdM=n,所以由文献[7,命题2.7]知Gpd(K0⊕K00)=n−1.因此由归纳假设知GpdK0≤n−1.故GpdM0≤n.

引理2.6(1)设G是A中的Gorenstein内射对象,则对任意的

(2)设G是A中的Gorenstein投射对象,则对任意的X∈,

证只证(1),(2)可对偶地证明.

(1)设G是A中的Gorenstein内射对象,则对任意的i≥0,存在A中的短正合序列GiIiGi−1,其中G0=G,Ii∈I.设X∈,则有Abel群同构

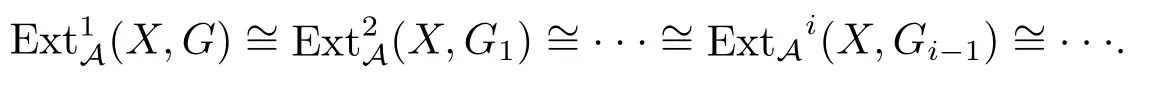
因为X的投射维数有限,所以

命题2.7设M是A中的对象.

(1)如果,那么GidM=idM.

(2)如果M,那么GpdM=pdM.

证(1)显然GidM≤idM.下证GidM≥idM.若GidM=∞,则结论成立.现设GidM<∞.若M∈GI,则存在一个短正合序列M0E‡M,其中M0∈GI,E∈I.因为所以由引理2.6知因此E∼=M0⊕M.因为E∈I,所以由文献[8,注记11.8]知M∈I.

设GidM>0,则由文献[7,命题2.7]的对偶知存在A中的短正合序列MGL,其中G∈GI,idL=GidM−1.因为G∈GI,所以存在一个短正合序列G0EG,其中G0∈GI,E∈I.因为EG是一个可许满态射,所以由及文献[8,命题2.15]可以得到如下行、列正合的交换图

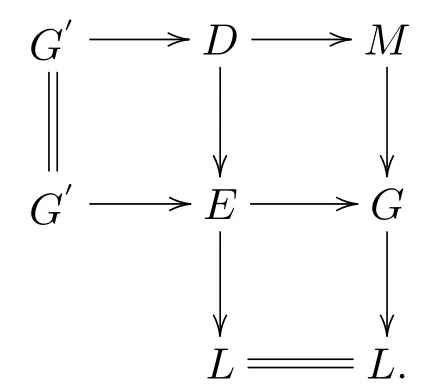
因为E∈I,所以idD≤idL+1=GidM.因为M,所以由引理2.6可知因此短正合序列可裂,故idM≤idD≤GidM.

(2)对偶地可以证明.

命题2.8设是非负整数,则以下等价

(1)GpdM≤n.(2)对任意的和任意的

(3)对任意的Q∈P和任意的

(4)对A中任意的正合序列则Kn∈GP.

证(2)⇒(3)显然.(4)⇒(1)由文献[7,命题2.7]可知.

(1)⇒(2)假设GpdM≤n,则存在A中的正合序列

其中G0,···,Gn是A中的Gorenstein投射对象.设L∈,则对任意的i>0,由文献[7,引理2.3]知

(3)⇒(4)考察A中的正合序列

其中G0,...,Gn−1是A中的Gorenstein投射对象.因为GpdM<∞,所以GpdKn<∞,因此有A中的正合序列

引理2.9设sup{GpdM|M∈A}<∞,则对任意的非负整数n,以下等价

(1)sup{GpdM|M∈A}≤n.

(2)对任意的idP≤n.

证由引理1.2的对偶和命题2.8可得.

定义2.10设M∈A.称M是强Gorenstein投射的,如果存在正合序列

其中P∈P,使得短正合序列是HomA(−,P)-正合的,其中f=em.称P是强完全投射分解.

对偶地可以定义A中的强Gorenstein内射对象和强完全内射分解.

注2.11对象M∈A是强Gorenstein投射的当且仅当存在一个短正合序列MPM,其中P是投射的,并且对任意的

命题2.12设A是正合范畴,且A有可数直和(直积),则对任意的M∈A,M∈GP(M∈GI)当且仅当M是A中某个强Gorenstein投射(内射)对象的直和项.

证只证Gorenstein投射的情形,Gorenstein内射的情形对偶地可以证明.

必要性设M是A中的Gorenstein投射对象,则存在一个完全投射分解

使得对任意的n∈Z,存在短正合序列KnPn−1Kn−1,其中Pn−1∈P,M=K0.对任意的m∈Z,用ΣmP表示这样的正合序列对任意的由文献[8,命题2.9,推论11.6]知有A中投射对象的正合序列

从而有短正合序列K⊕PiK,M是K的直和项.设L∈P,则由

知HomA(Q,L)正合.因此Q是强完全投射分解,故M是强Gorenstein投射对象K的直和项.

充分性由命题2.4可得.

定理2.13设A是正合范畴,且A有可数直和与可数直积.则

证设n≥0,且sup{GpdM|M∈A}≤n.下面证明sup{GidM|M∈A}≤n.首先证明若M是A中的强Gorenstein投射对象,则GidM≤n.设M∈A是强Gorenstein投射的,则由注2.11知存在一个短正合序列MPM,其中P∈P.由文献[8,定理12.8]的对偶可得如下行、列正合的交换图

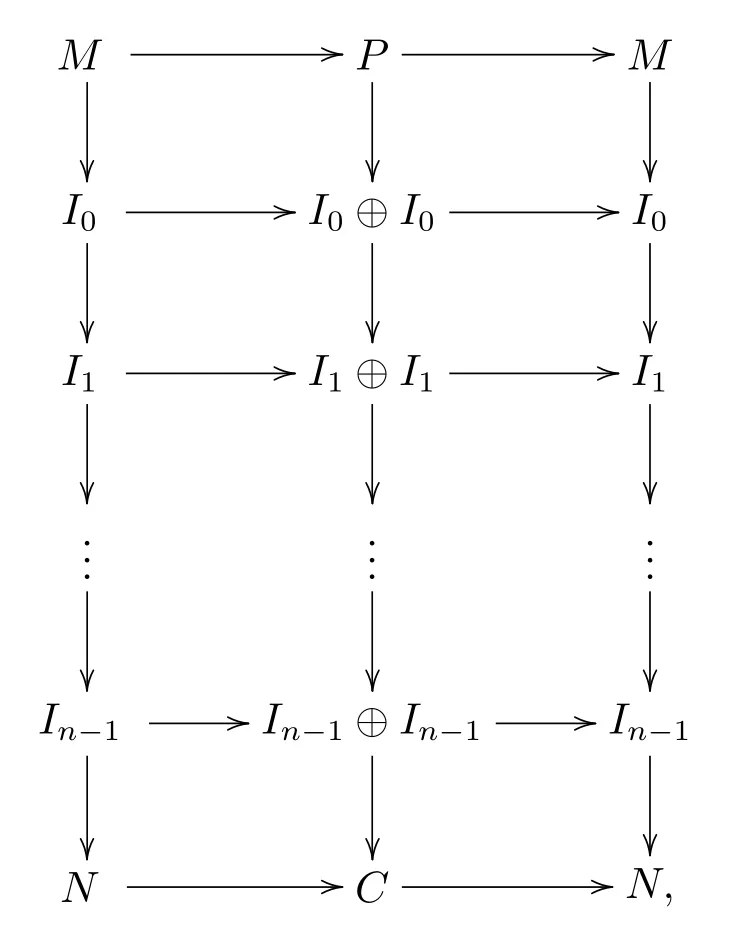
其中Ii是内射的,i=0,···,n−1.因为P是投射的,由引理2.9知idP≤n,所以由命题1.2的对偶知C∈I.设E是A中的内射对象,则由命题2.7知pdE≤n,所以对任意的i≥n+1,因此由注2.11的对偶知N是强Gorenstein内射的.故GidM≤n.

其次证明对任意的M∈A,GidM≤n.

设M∈A,由条件知GpdM=m≤n.下面对m进行归纳.

当m=0时,M是Gorenstein投射的.由命题2.12,存在A中的强Gorenstein投射对象G,使得M是G的直和项.由第一步知GidG≤n.由命题2.5的对偶知GidM≤n.

设m≥1.由文献[7,命题2.7]知存在短正合序列KNM,其中N∈GP,GpdK≤m−1.由归纳假设知GidK≤n,GidN≤n.于是由文献[8,定理12.8]的对偶,命题2.8的对偶和文献[7,定理2.4]的对偶知GidM≤n.

对偶地可证若sup{GidM|M∈A}≤n,则sup{GpdM|M∈A}≤n.故结论成立.

设A是有足够多投射对象,足够多内射对象以及可数直和与可数直积的正合范畴.令

称GgdimA为A的整体Gorenstein维数.

3 正合范畴中的Gorenstein导出函子

定义3.1设M∈A,对象M的真左Gorenstein投射分解是一个正合序列

其中每个Gi∈GP,并且对任意的i≥0,短正合序列Ki+1GiKi是HomA(GP,−)-正合的,即对任意的G∈GP,序列

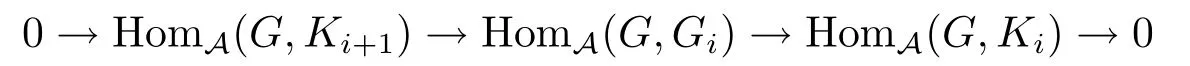
正合,其中K0=M.

定义3.2设且GM是M的一个真左Gorenstein投射分解.对任意的i≥0及任意的N∈A,定义

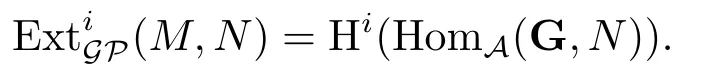
由比较定理(文献[8,定理12.4]和文献[11,P175])知的定义合理.

对偶地,可以定义A中对象的余真右Gorenstein内射分解,且由文献[7,命题2.7,引理2.3]的对偶知A中每个Gorenstein内射维数有限的对象都有余真右Gorenstein内射分解.于是对任意的任意的M∈A及i≥0,可以合理地定义.

命题3.3(1)设A中的对象M有有限投射维数,则对任意的N∈A及任意的i≥0,.

(2)设A中的对象N有有限内射维数,则对任意的M∈A及任意的i≥0,.

证(1)设pdM=n<∞,则M有长度为n的投射分解

设 0≤i≤n−1,则短正合序列Ki+1PiKi中每一项都有有限投射维数.设G是A中的一个Gorenstein投射对象,用HomA(G,−)作用在上述短正合序列上,由文献[7,引理2.3]知序列

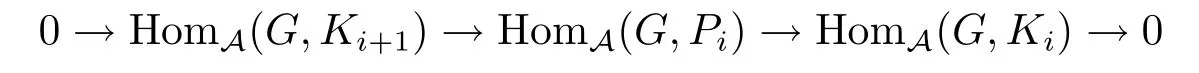
正合.这表明M的投射分解是M的真左Gorenstein投射分解.故对任意的N∈A及任意的i≥0,.

(2)对偶地可以证明.

定理3.4设M,N∈A.若M的Gorenstein投射维数有限,N的Gorenstein内射维数有限,则对任意的i≥0,.

证设GpdM<∞,则由文献[7,命题2.7]知M有真左Gorenstein投射分解G‡M,且存在A中的短正合序列,其中G0∈GP,pdK1=GpdM−1.设H是A中的Gorenstein内射对象,则存在A中的短正合序列其中E∈I,H0∈GI.因为K1的投射维数有限,所以由引理2.6知故序列

正合.于是对任意α∈HomA(K1,H),存在β∈HomA(K1,E),使得α=tβ.又因为E∈I,所以序列

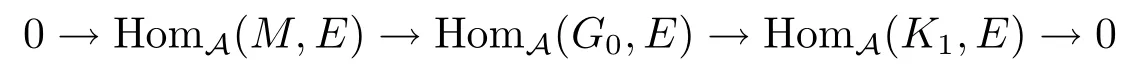
正合.故存在γ∈HomA(G0,E),使得β=γf.因此有以下交换图

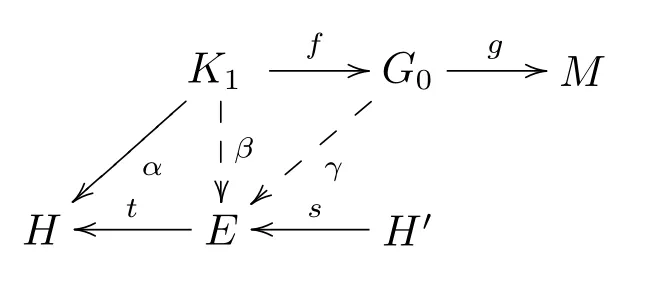
令δ=tγ.则δ∈HomA(G0,H),且α=δf.所以

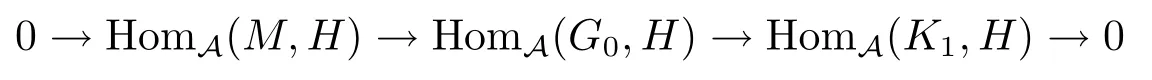
正合.继续该过程可知M的Gorenstein投射分解GM是HomA(−,GI)-正合的.同理可以证明N的余真右Gorenstein内射分解NH是HomA(GP,−)-正合的.于是有交换图

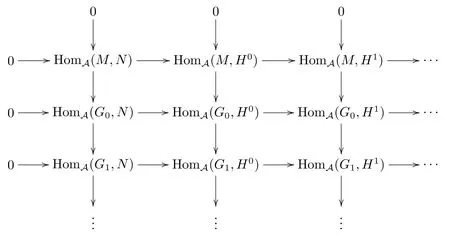
其中除第一行和第一列外,其他行和列均正合.由文献[11,命题1.4.16]知,对任意的i≥0,定理证毕.

由定理3.4,对M,N∈A,若GpdM<∞,GidN<∞,则记

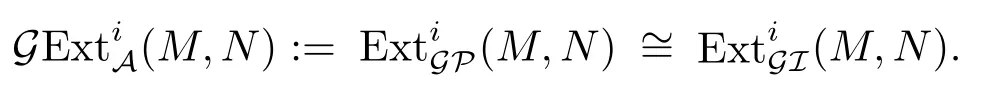
命题3.5设sup{GidN|N∈A}<∞,M∈GfP,则对任意的n≥0,下列条件等价

(1)GpdM≤n.

(2)对任意的N∈A和任意的i>0,.

(3)对任意的N∈A,.

(4)对任意的Q∈P,.

证(1)⇒(2)⇒(3)⇒(4)显然.下证(4)⇒(1).

设Q是A中的投射对象,由命题2.7知idQ=GidQ.因为sup{GidN|N∈A}<∞,所以idQ=GidQ<∞.由命题3.3知. 由命题 2.8 知GpdM≤n.

对偶地有

命题3.6设sup{GpdN|N∈A}<∞,则对任意的n≥0,下列条件等价

(1)GidN≤n.

(2)对任意的M∈A和任意的i>0,.

(3)对任意的M∈A,.

(4)对任意的E∈I,.