NONCONFORMING FINITE ELEMENT METHOD FOR THE NONLINEAR KLEIN-GORDON EQUATION WITH MOVING GRIDS

ZHANG Fei-ran,ZHU Yan

(School of Mathematics and Statistics,Shangqiu Normal University,Shangqiu 476000,China)

Abstract:In this paper,the nonlinear Klein-Gordon equation is studied.By using the Crank-Nicolson moving grid nonconforming finite element method,the traditional Riesz projection operator is not needed,interpolation techniques and special properties of the element are used to obtain the corresponding convergence analysis and optimal error estimation.

Keywords:Klein-Gordon equation;anisotropy;moving grids;nonconforming;Crank-Nicolson scheme

1 Introduction

Moving grids method has important applications in a variety of physical and engineering areas such as solid and fluid dynamics,combustion,heat transfer,material science,etc.This method is more efficient than the fixed grids and does not increase computing cost.We usually apply the finite element methods to the spatial domain,but choose difference methods with respect to the time variable for solving evolution partial differential equations.At the same time,different meshes of domain are used at different time level.

Several moving grids techniques were studied.Such as[1]considered the moving grids finite element method;[2]and[3]constructed and analyzed this method for the oil-water two-phase displacement problem;[4–8]analyzed the parabolic,Stokes problems,parabolic integro-differential equations,generalized nerve conductive equations and fractional diffusion equations with moving grids nonconforming finite element scheme respectively.But the analysis in the above studies relies on the regular condition or quasi-uniform assumption for meshes.

The Klein-Gordon equation is the most basic equation used in relativistic quantum mechanics and quantum field theory to describe a spin-zero particle.The equation is closely related to the physical problem and plays an important role in the study of soliton.In[9],authors studied the existence of a unique global solution under the condition that the parameter is small enough.In[10],a display difference scheme was established for one-dimensional Klein-Gordon equation of unbounded region,and the results of stability and convergence of the scheme were obtained by the energy analysis method.In[11],the numerical solution of one-dimensional Klein-Gordon equation was studied.However,the finite element method for the Klein-Gordon equation is rare.

In this paper,we mainly focus on the convergence theory,the finite element method of moving grids is introduced,and the Crank-Nicolson discrete scheme of the nonlinear Klein-Gordon equation is analyzed without requiring the subdivision to satisfy the regular hypothesis,and the corresponding optimal error estimation of the moving grid approach is derived.It is worth mentioning that,in the usual finite element method of moving meshes,it is necessary to use the Riesz projection to approximate the solution of the original problem,and this paper makes use of the particularity of the element structure,that is,u−Πuand the elements in the finite element space are orthogonal in the sense of energy mode,and the Riesz projection is used to simplify the proof process of the previous documents.

2 Element Construction

3 The Moving Grids Approximation of Crank-Nicolson Discretization Scheme

We consider the nonlinear Klein-Gordon equation

whereX=(x,y),α>0,γ>0,g(u)satisfies the Lipschitz continuous conditionon on the variableu,and has the second order bounded partial derivative.

Letut=Q,(3.1)is equivalent to the following question

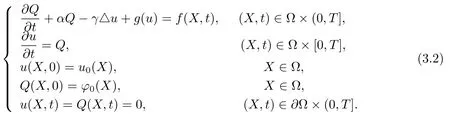
The variational formulation for problem(3.2)is written as:

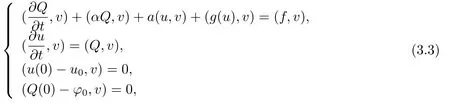
Then the approximation problem corresponding to(3.3)reads as:finduh,Qh∈Vh,∀vh∈Vh,such that

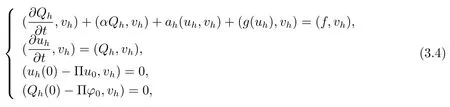
In this section we apply the idea of moving grids to problem(3.4)and develop the Crank-Nicolson discretization scheme for anisotropic finite element.Let 0=t0

Now,we introduce the Crank-Nicolson discretization scheme of anisotropic finite element to determine the function valuesas follows

4 Error Estimates

The main error between the solutionu(X,t)and the approximation solutionuh(X,t)consists of three parts:the interpolation error with respect to the finite element method,the difference error with respect to the time,and the error of moving grids.