FEKETE-SZEG PROBLEMS FOR SEVERAL QUASI-SUBORDINATION SUBCLASSES OF ANALYTIC AND BI-UNIVALENT FUNCTIONS ASSOCIATED WITH THE DZIOK-SRIVASTAVA OPERATOR
2020-08-13LONGPinhongLIXingWANGWenshuai
LONG Pin-hong,LI Xing,WANG Wen-shuai
(School of Mathematics and Statistics,Ningxia University,Yinchuan 750021,China)
Abstract:In the article we introduce two quasi-subordination subclasses of the function classof analytic and bi-univalent functions associated with the Dziok-Srivastava operator,and some problems for their coefficient estimation and Fekete-Szeg functional.By using differential quasisubordination and convolution operator theory,we obtain some results about the corresponding bound estimations of the coefficient a2 and a3 as well as Fekete-Szeg functional inequalities for theses subclasses,which generalize and improve some earlier known results.
Keywords:Fekete-Szeg problem;bi-univalent function;Gaussian hypergeometric function;Dziok-Srivastava operator;quasi-subordination
1 Introduction
In the article,our aim focuses on the certain quasi-subordination subclasses of analytic and bi-univalent functions associated with the Dziok-Srivastava operator.To state our results,at first we will recall some notations and basic properties for analytic and bi-univalent functions and Dziok-Srivastava operator.
LetAbe the class of normalized analytic functionf(z)by

in the open unit disk∆={z∈C:|z|<1}.
Let the subclassSofAbe the set of all univalent functions in∆.According to the Koebe one quarter theorem[1],the inversef−1of everyf∈Ssatisfies

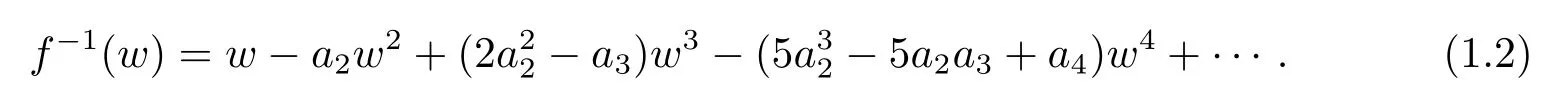
If both the functionf∈Aand its inversef−1are univalent in∆,then it is bi-univalent.Denote by Σ the class of all bi-univalent functionsf∈Ain∆.
For givenf,g∈A,define the Hadamard product or convolutionf∗gby

wheref(z)is given by(1.1)andAssume that the Gaussian hypergeometric functionqFs(α1,···,αq;β1,···,βs;z)is defined by

for the complex parametersαkandβjwithβj60,−1,−2,−3,...(k=1,···,q;j=1,···,s),where(‘)ndenotes the Pochhammer symbol or shifted factorial by

Dziok and Srivastava[2,3]ever introduced the convolution operatorqIs(α1,···,αq;β1,···,βs)=qIslater named by themselves as follows

where
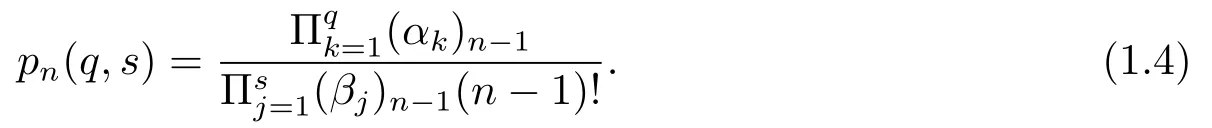
Note that
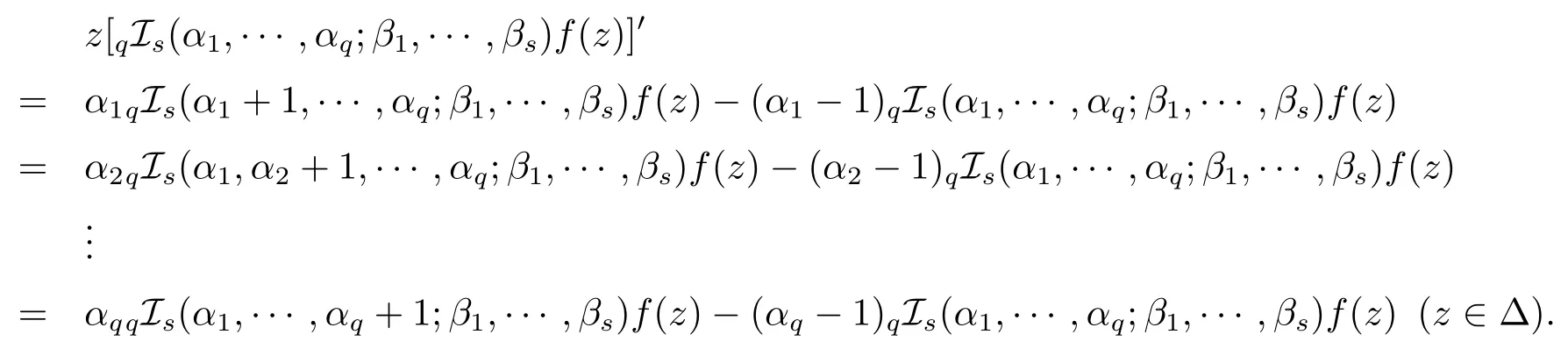
Here we remind some reduced versions of Dziok-Srivastava operatorqIs(α1,···,αq;β1,···,βs)for suitable parametersαk(k=1,···,q)andβj(j=1,···,s);refer to the generalized Bernardi operatorJη=2I1(1,1+η;2+η)(<(η)>−1)[4];Carlson-Shaffer operatorL(a,c)=2I1(a,1;c)[5];Choi-Saigo-Srivastava operatorIλ,µ=2I1(µ,1;λ+1)(λ>−1,µ≥0)[6];Hohlov operator;Noor integral operatorIn=2I1(2,1;n+1)[9];Owa-Srivastava fractional differential operator;Ruscheweyh derivative operatorDδ=2I1(1+δ,1;1)[12].
In 1967,Lewin[13]introduced the analytic and bi-univalent function and proved that|a2|<1.51.Moreover,Brannan and Clunie[14]conjectured thatand Netanyahu[15]obtained thatLater,Styer and Wright[17]showed that there exists functionf(z)so thatHowever,so far the upper bound estimate|a2|<1.485 of coefficient for functions inby Tan[18]is best.Unfortunately,as for the coefficient estimate problem for every Taylor-Maclaurin coefficient|an|(n∈N{1,2})it is probably still an open problem.Based on the works of Brannan and Taha[19]and Srivastava et al.[20],many subclasses of analytic and bi-univalent functions classwere introduced and investigated,and the non-sharp estimates of first two Taylor-Maclaurin coefficients|a2|and|a3|were given;refer to Deniz[21],Frasin and Aouf[22],Hayami and Owa[23],Patil and Naik[24,25],Srivastava et al.[26,27],Tang et al.[28]and Xu et al.[29,30]for more detailed information.Recently,Srivastava et al.[31,32]gave some new subclasses of the function classof analytic and bi-univalent functions to unify the works of Deniz[21],Frasin[33],Keerthi and Raja[34],Srivastava et al.[35],Murugusundaramoorthy et al.[36]and Xu et al.[29],etc.Besides,we also refer to Goyal et al.[37]for the subclasses of analytic and bi-univalent associated with quasi-subordination.Since Fekete-Szeg[38]studied the determination of the sharp upper bounds for the subclass ofS,Fekete-Szegfunctional problem was considered in many classes of functions;refer to Abdel-Gawad[39]for class of quasi-convex functions,Koepf[40]for class of close-to-convex functions,Orhan and Rducanu[16]for class of starlike functions,Magesh and Balaji[41]for class of convex and starlike functions,Orhan et al.[42]for the classes of bi-convex and bi-starlike type functions,Panigrahi and Raina[43]for class of quasi-subordination functions,Tang et al.[28]for classes of m-mold symmetric bi-univalent functions.In addition,Murugusundaramoorthy et al.[36,44,45]and Patil and Naik[46]ever introduced and investigated several new subclasses of the function classof analytic and bi-univalent functions involving the hohlov operator.Moreover,Al-Hawary et al.[47]studied the Fekete-Szegfunctional problem for the classes of analytic functions of complex order defined by the Dziok-Srivastava operator.Motivated by the statements above,in the article we are ready to introduce and investigate two new subclasses of the function classof analytic and bi-univalent functions associated with the Dziok-Srivastava operator and quasi-subordination,and consider the corresponding bound estimates of the coefficienta2anda3as well as the corresponding Fekete-Szegfunctional inequalities.Furthermore,the consequences and connections to some earlier known results would be pointed out.
For two analytic functionsfandg,if there exist two analytic functionsϕandhwith|ϕ(z)|≤1,h(0)=0 and|h(z)|<1 forz∈∆ so thatf(z)=ϕ(z)g(h(z)),thenfis quasi-subordinate tog,i.e.,f≺quasig.Note that ifϕ≡1,thenfis subordinate togin∆,i.e.,f≺g.Further,ifh(z)=z,thenfis majorized bygin∆,i.e.f≤g.For the related work on quasi-subordination,refer to Robertson[48],and Frasin and Aouf[22].Write

First we will introduce the following general subclasses of analytic and bi-univalent functions associated with the Dziok-Srivastava operator.
Definition1.1A functionf(z)∈given by(1.1),belongs to the classif the following quasi-subordinations are satisfied
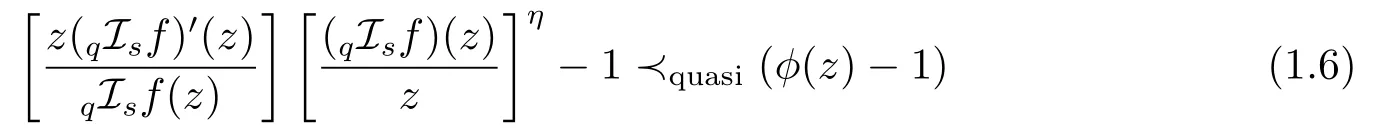
and
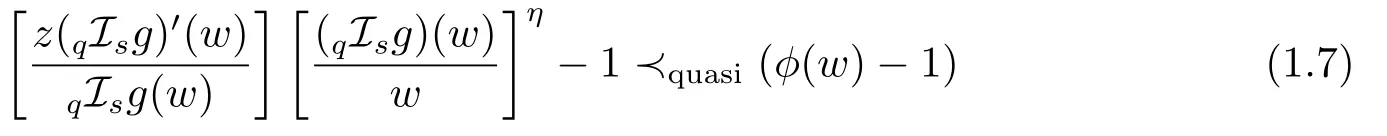
forz,w∈∆,whereη ≥0 and the functiongis the inverse offgiven by(1.2).
Definition 1.2A functiongiven by(1.1),belongs to the classif the following quasi-subordinations are satisfied:
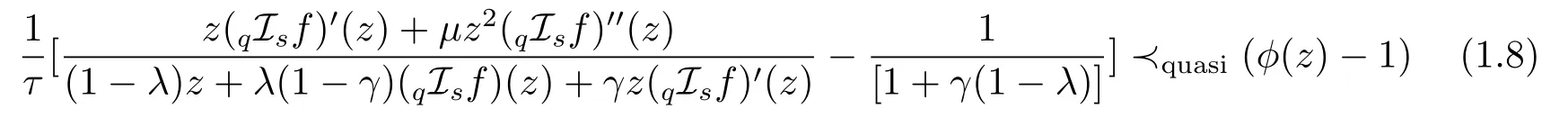
and

forz,w∈∆,whereτ∈C{0},0≤µ≤1,0≤λ≤1,0≤γ≤1 and the functiongis the inverse offgiven by(1.2).
Lemma 1.3(see[1,49])LetPbe the class of all analytic functionsq(z)of the following form
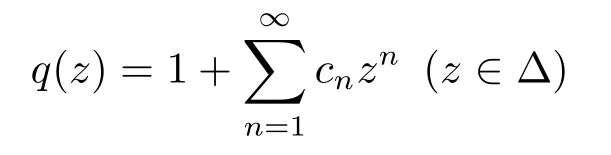
satisfying
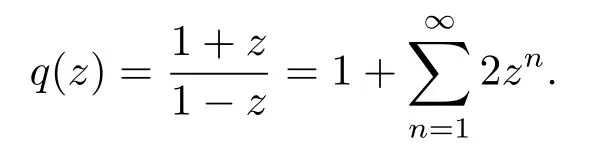
2 Coefficient Bounds for the Function Class
Denote the functionssandtinPby

Equivalently,from(2.1)we know that

and

Givenφ∈Pwithφ0(0)>0,letφ(∆)be symmetric with respect to the real axis.When the series expansion form ofφis denoted by

by(2.2)–(2.3)and(2.4)it follows that

and

In the section we study the estimates for the class.Now,we establish the next theorem.
Theorem 2.1Iff(z)given by(1.1)belongs to the class,then
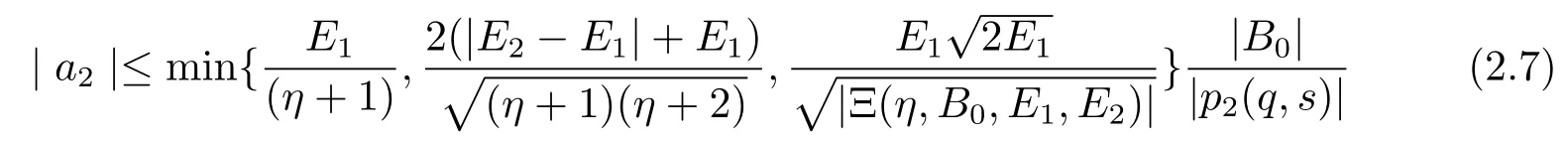
and

where

ProofIfthen by Definition 1.1 and Lemma 1.3,there exist two analytic functionsu(z)andv(w)∈Pso that
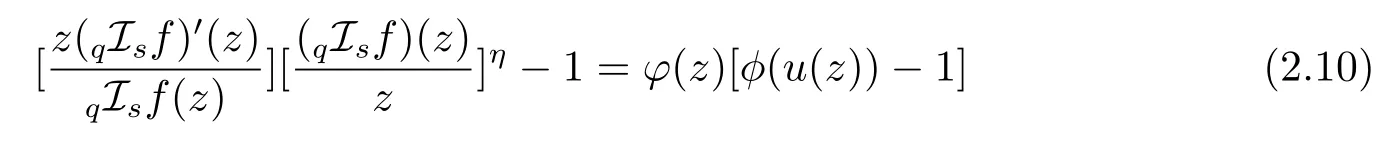
and

Expanding the left half parts of(2.11)and(2.12),we obtain that

and
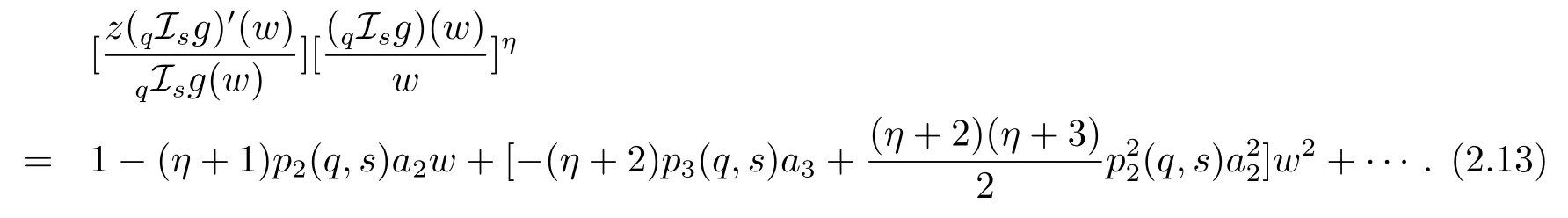
In addition,we know that
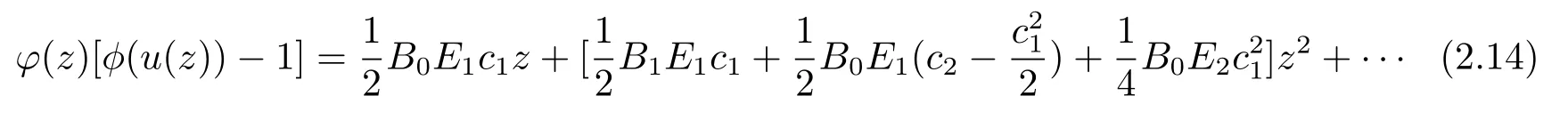
and

Therefore,from(2.10)–(2.15)we have that

and
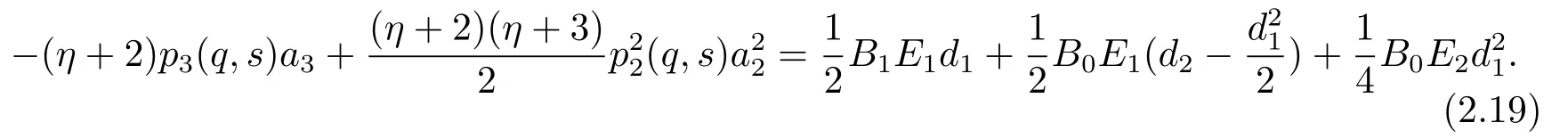
From(2.16)and(2.18),it infers that

Then,we show that

and

By(2.17)and(2.19),we have that
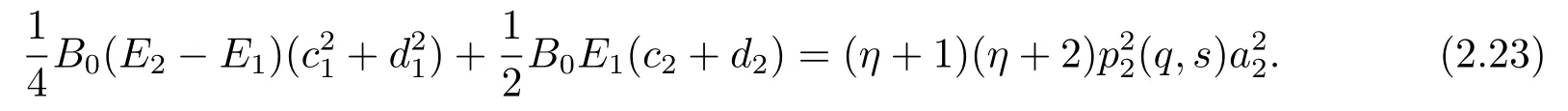
Therefore,by(2.22)–(2.23)we obtain that
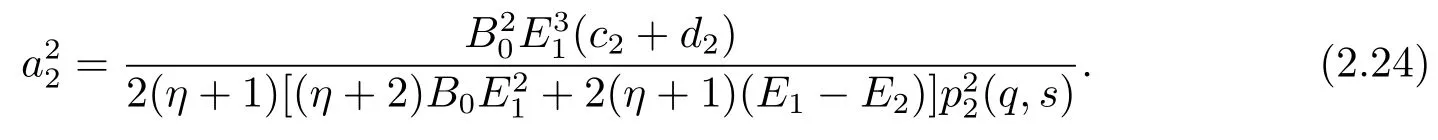
We follow from Lemma 1.3 and(2.22)–(2.24)that

and
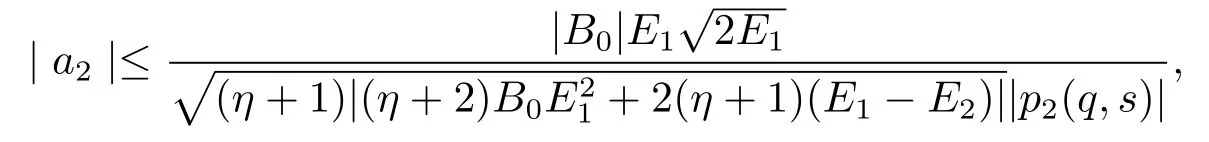
then(2.7)holds.Similarly,from(2.17),(2.19)and(2.21),it also implies that

Hence,from(2.22)and(2.25),we obtain that

Therefore,from Lemma 1.3 it shows that
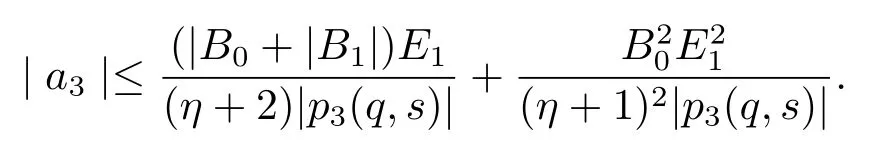
On the other hand,by(2.23)and(2.25),we infer that
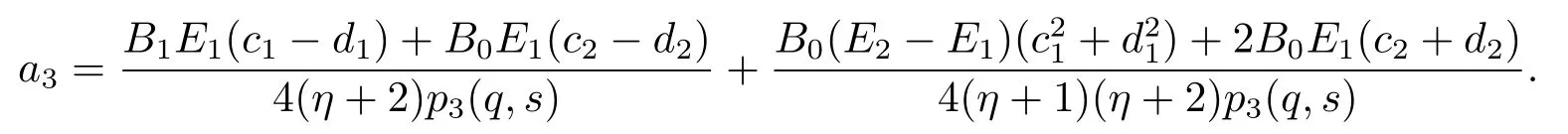
Thus,from Lemma 1.3,we see that

Next,we consider Fekete-Szegproblems for the class.
Theorem 2.2Iff(z)given by(1.1)belongs to the classandδ∈R,then
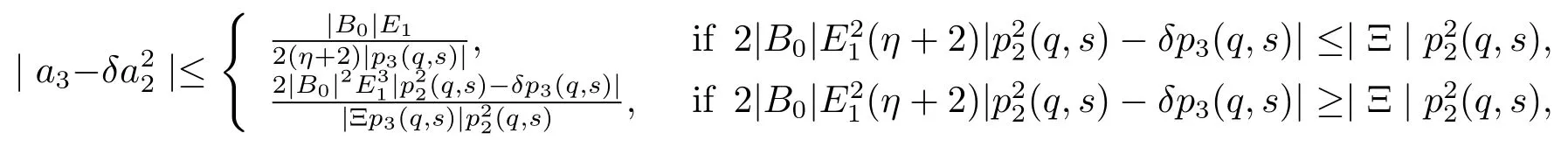
ProofFrom(2.25),it follows that
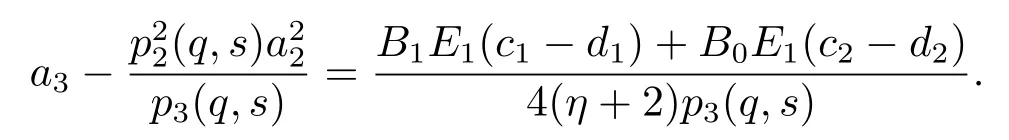
By(2.24)we easily obtain that
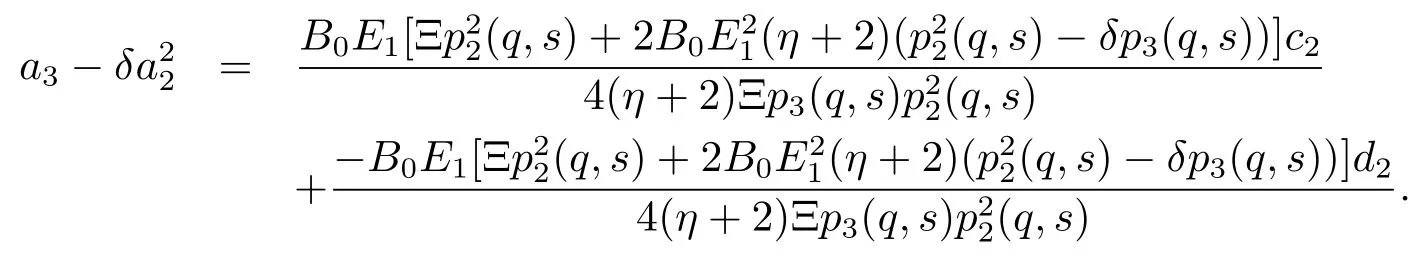
Hence,from Lemma 1.3,we imply that

Corollary 2.3Iff(z)given by(1.1)belongs to the classandδ∈R,then
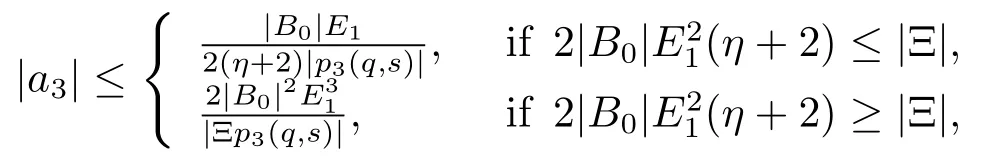
Remark 2.4Without quasi-subordination(i.e.,ϕ(z)≡1),if we choose some suitable parametersαk(k=1,···,q),βj(j=1,···,s)andη,we obtain the following reduced versions forin Theorem 2.1.
Remark 2.5Without Dziok-Srivastava operator,we can collect the following reduced versions forin Theorem 2.1.
3 Coefficient Bound Estimates for the Function Class
Now,we study the coefficients for the classand establish the next theorem.
Theorem 3.1Iff(z)given by(1.1)belongs to the class,then

for

and

and

for

and

where

and

ProofHere,we follow the method of Theorem 2.1.Ifthen by Definition 1.2 there exist two analytic functionsu(z),v(z):∆→∆withu(0)=0 andv(0)=0 such that

and

Expanding the left half parts of(3.5)and(3.6),we have that

and

Therefore,From(2.14)–(2.15)and(3.5)–(3.8),we get that
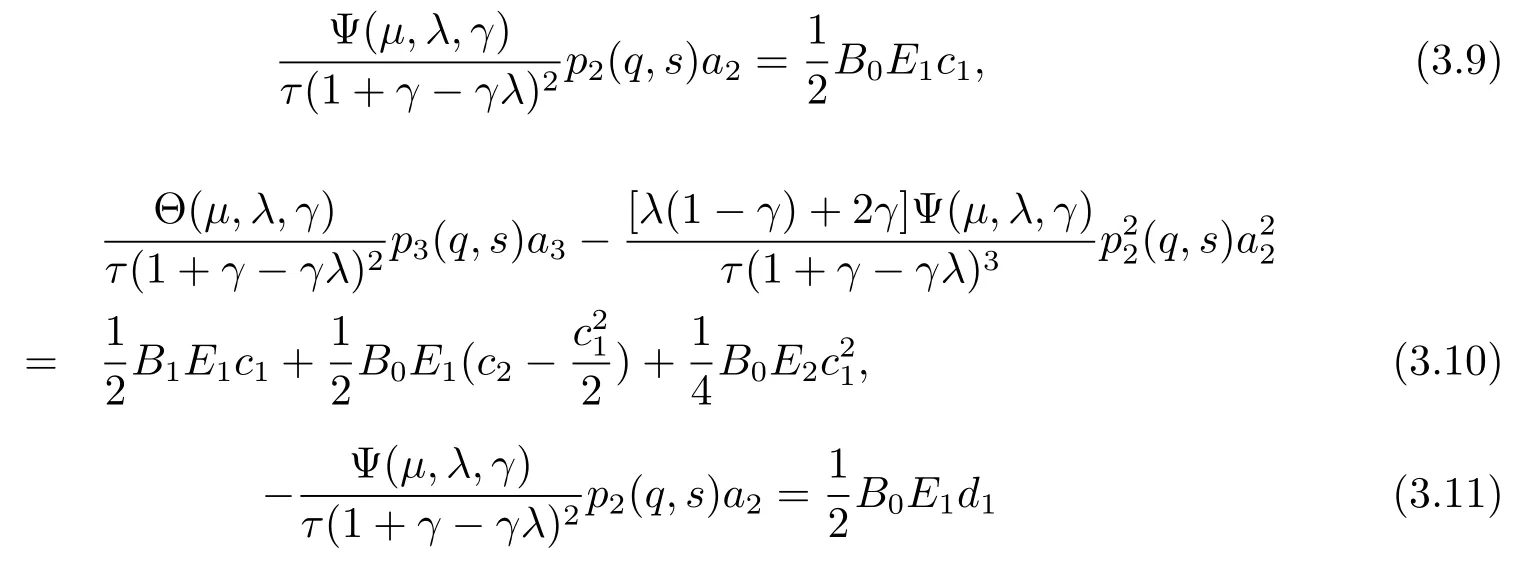
and

From(3.9)and(3.11),we know that

Then,it infers that

and

By(3.10)and(3.12),we have that

Therefore,by(3.15)–(3.16)we know that
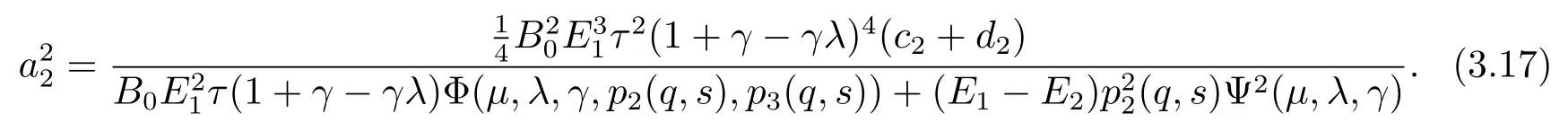
Therefore,from(3.15)–(3.17)and Lemma 1.3,we obtain that
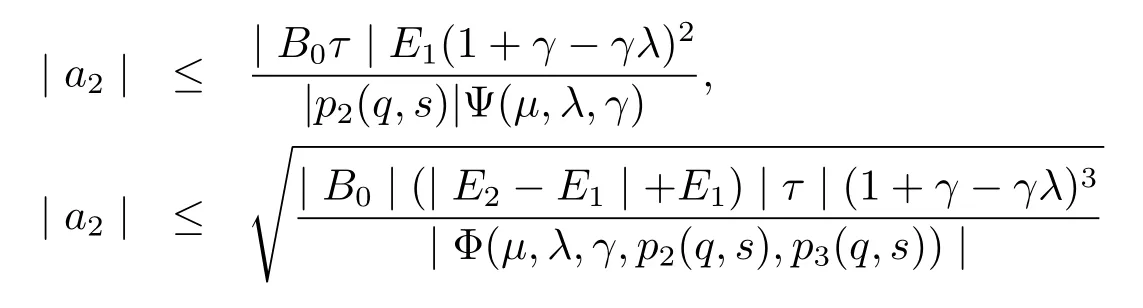
and
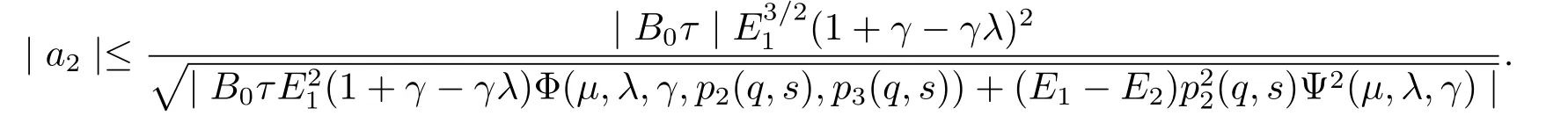
Similarly,from(3.10)and(3.12),it implies that
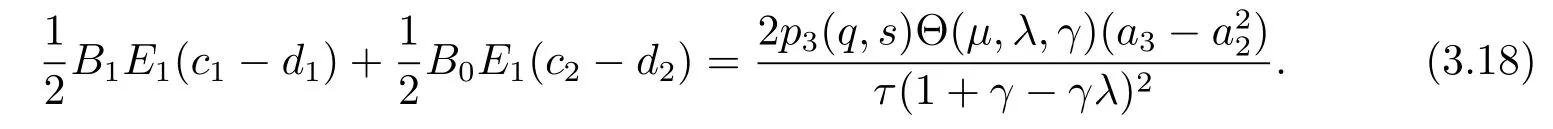
Hence,by(3.15)and(3.18),it follows that
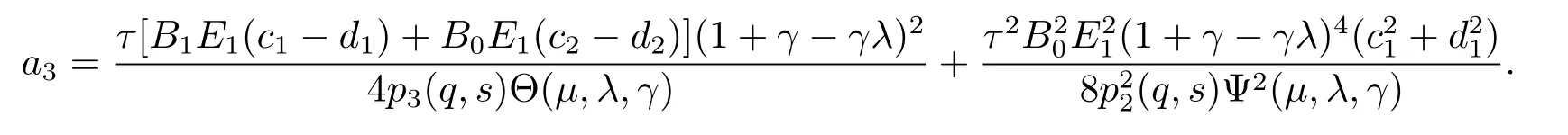
So,we obtain from Lemma 1.3 that
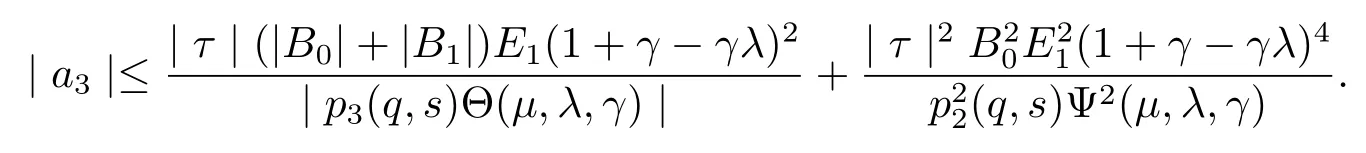
On the other hand,by(3.16)and(3.18),we infer that

Thus,from Lemma 1.3 we see that

Next,we consider Fekete-Szegproblems for the class.
Theorem 3.2Letf(z)given by(1.1)belong to the classandδ∈R.Then

if

or

if

where Φ = Φ(µ,λ,γ,p2(q,s),p3(q,s)),Θ = Θ(µ,λ,γ)and Ψ = Ψ(µ,λ,γ)are the same as in Theorem 3.1.
ProofFrom(3.18),it follows that


