无巧不成锥*
——一道课本习题的再探讨
2020-08-13江苏省苏州市苏州学府中学215000蒋惠丽
江苏省苏州市苏州学府中学(215000) 蒋惠丽
本文对苏教版义务教育教科书《数学》九年级上册课本第86 页“圆锥的侧面积”中的一道习题作了探讨,并得到一些结论,供各位同仁在设计与该题相关的“拓展与延伸”教学时参考.
1 原题展示
(1)求这个扇形的面积(结果保留π);
(2)用所剪的扇形纸片围成一个圆锥的侧面,能否从剪下的3 块余料中选取一块,剪出一个圆作为这个圆锥的底面?[1]
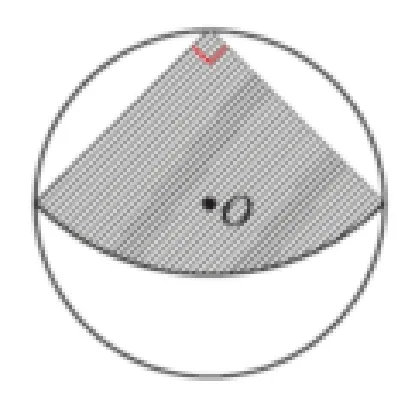
图1
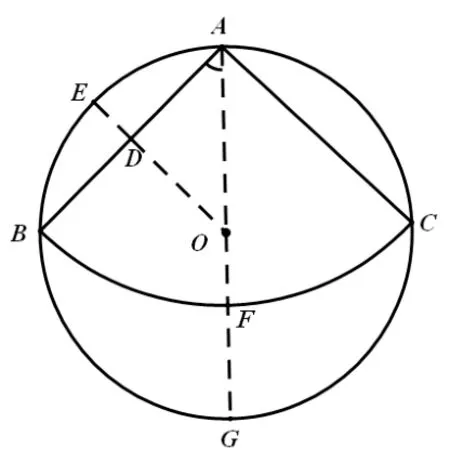
图2
2 思路呈现
对学生而言,本题还是有一定难度的.解决本题的关键是抓住能够围成圆锥的侧面与底面的关系——扇形的弧长等于底面圆的周长.根据题目所给条件,不难算出扇形的半径为2,扇形的弧长=×2π=π,下面就是考虑剪下的3 块余料中选取哪一块,我们考虑底面圆的直径,如图2,过点O作OD⊥AB于点D,延长OD交⊙O于点E,同时延长AO交弧BC于点F,交⊙O于点G,容易求得线段DE的长度为-1,线段FG的长度为-2,显然FG>DE,那么可剪的最大的圆的直径为-2,周长为因此不能剪出一个圆作为这个圆锥的底面.
3 拓展思考
我们已知道,当扇形圆心角为90°时,不能从3 块余料中剪出一个圆作为这个圆锥的底面,那么究竟当扇形圆心角为多少度时就可以呢?围绕这个问题,我们可以展开一些探索活动.如图3所示,为了计算方便,不妨假设圆心角为2θ(0°<θ<90°),⊙O的半径为1.与90°的情形类似,如图4,连接AO,根据图形的对称性可得∠OAB=θ.我们把线段DE的长度记为d1,线段FG的长度记为d2,d1、d2究竟谁大呢?下面我们把d1、d2用含θ的代数式表示出来,通过比较再作判断.
在RtΔOAD中,∠OAB=θ,OA=1,解这个直角三角形得AD=cosθ,OD=sinθ,从而可知扇形ABC的半径为2 cosθ,d1=1-sinθ;另一方面,d2=AG-AF=2-2 cosθ.我们利用作差比较d1和d2的大小关系,令Δd(θ)=d1-d2,那么Δd(θ)=(1-sinθ)-(2-2 cosθ)=2 cosθ-sinθ-1,因为Δd′(θ)=-2 sinθ-cosθ<0,所以Δd(θ)是关于θ的单调递减函数,即Δd(θ)随着θ的增大而减小,因此我们只要找到函数Δd(θ)的零点即可.
不妨设Δd(θ0)=2 cosθ0-sinθ0-1=0,利用GeoGebra 软件求方程的近似解,可求得满足条件的θ0≈36.7°.从而,当0°<θ<θ0时,d1>d2,圆锥底面圆的直径最大可取d1;当θ0<θ<90°时,d1<d2,圆锥底面圆的直径最大可取d2;当θ=θ0时,d1=d2,圆锥底面圆的直径最大可取d1或d2.
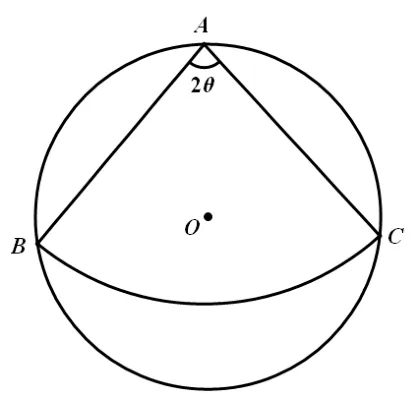
图3
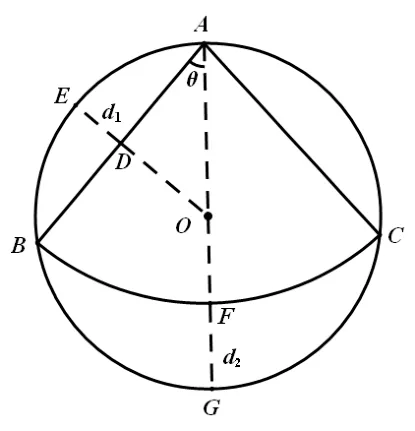
图4
接下来,我们研究当θ为何值时,剩下3 块余料中剪出的一个圆能否作为这个圆锥的底面?
当θ=θ0时,d1=d2=1-sinθ0≈0.4,扇形的半径AB=2 cosθ0≈1.6,弧BC的长度≈×1.6=0.65π,而底面圆周长最多为0.4π<0.65π,因此当扇形圆心角为2θ0时,剩下3 块余料中剪出的一个圆作为这个圆锥的底面.
当0°<θ<θ0时,d1>d2,d1=1-sinθ,扇形的半径AB=2 cosθ,弧BC的长度=×2 cosθ=而底面圆周长最多为(1-sinθ)π,若要剪出的圆可以作为这个圆锥的底面,必须满足底面圆周长=弧BC的长度,因此有(1- sinθ)π ≥当θ≈θ1<θ0时,(1-sinθ)π=为了画图方便,把45°转化成弧度观察GeoGebra 中得到的函数图像,如图5,θ1≈27.5°,而且当0<θ≤θ1时,(1-sinθ)π ≥即余料部分可以剪出一个圆作为这个圆锥的底面.
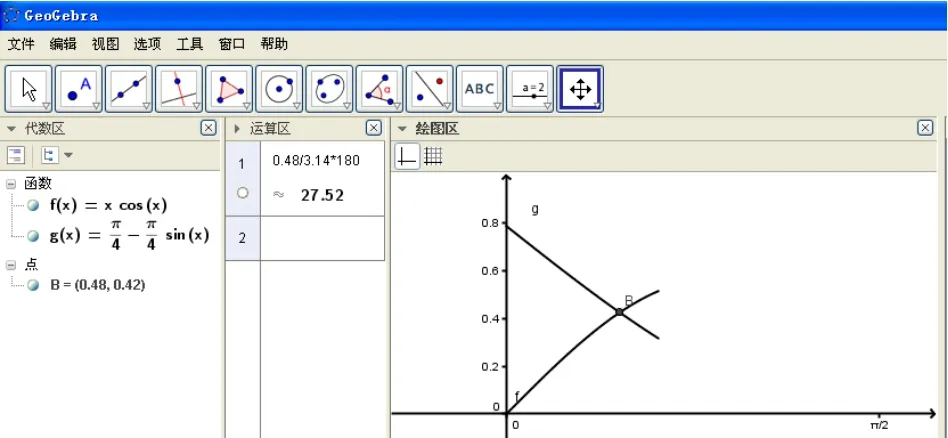
图5
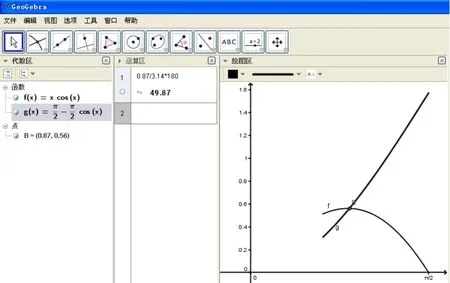
图6
同理,当θ0<θ<90°时,d1<d2,d2=2-2 cosθ,扇形的半径AB=2 cosθ,弧BC的长度=×2 cosθ=而底面圆周长最多为(2-2 cosθ)π,若要剪出的圆可以作为这个圆锥的底面,必须满足底面圆周长=弧BC的长度,因此有(2- 2 cosθ)π ≥当θ≈θ2>θ0时,(1- sinθ)π=观察GeoGebra中得到的函数图像,如图6,θ2≈50°,而且当θ2≤θ<90°时,(2-2 cosθ)π ≥即余料部分可以剪出一个圆作为这个圆锥的底面.
综上所述,我们知道当0°<θ≤θ1或θ2≤θ<90°(其中θ1≈27.5°,θ2≈50°)时,在被剪掉的3 块余料中,能从中选取一块剪出一个圆作为这个圆锥的底面.
4 延伸思考
从实用价值的角度来考虑,圆锥通常要考虑表面积一定时体积最大,或者体积一定时表面积最小,那么在这张半径为1 的圆形纸片中,怎样才能用所剪的扇形纸片围成一个体积最大的圆锥呢?我们考虑圆锥的体积V=πr2h,其中,r表示圆锥底面圆半径,h表示圆锥的高.
当θ取定时,如果在被剪掉的3 块余料中,能从中选取一块剪出一个圆作为这个圆锥的底面,与之对应的r也是唯一确定的,r=根据勾股定理知h=此时圆锥的体积可以表示为
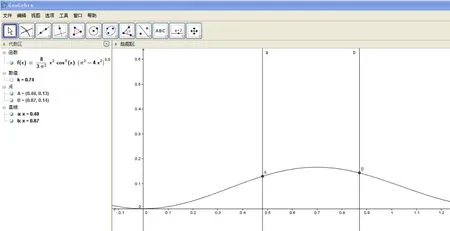
图7
如图7,我们从函数图像中可以看出,当0°<θ≤θ1(其中θ1≈27.5°) 时,V(θ) 在θ=θ1时取得最大值;当θ2≤θ<90°(θ2≈50°) 时,V(θ) 在θ=θ2时取得最大值.我们只要比较即可得出θ取何值时,圆锥的体积可以取得最大值.
