以形助数化难为易——坐标方法在解题中的应用

广东省肇庆市德庆县教育局教研室(526600) 张锦玲

坐标方法是16世纪数学重要的成果,是数学方法中最重要的方法之一,它是数形结合的桥梁,坐标方法的实质就是借助于点的坐标,运用解析工具将几何图形的位置关系转化为坐标关系进而再转化为数量关系.其实质是通过“以形助数”,使得复杂问题简单化,抽象问题具体化,使抽象思维和形象思维相结合,通过图形的描述、代数的论证来研究和解决数学问题的一种数学思想方法.

坐标方法也称解析法,它是通过平面直角坐标系的建立把问题代数化,由代数运算获得相关的代数结果,再通过坐标系转化为结论.坐标系的建立是坐标法引入的前提,有了坐标系,才能设点的坐标,进一步研究数量关系.中学教材最初的坐标系应该从数轴开始,新教材作为点坐标的引入从数轴到平面直角坐标系,使知识结构安排紧凑合理,符合了学生的从简单到复杂的认知心理结构,也使得坐标方法的提出更具有系统性,这为学生学习坐标方法奠定了坚实的基础.坐标方法使解决问题变得具有一定的程序可遵循,这种程序性使我们对某些灵活多变的数学问题寻求具体、简便的解决办法得到了优化,特别是对那些纯几何方法难以获解的问题,更能发挥其巨大的威力.

坐标方法的应用可谓无所不在,本文就坐标方法在中学数学解题中列举部分应用.

1 方程问题

例1:设关于x的方程ax2+(a+2)x+9a=0 有两个不等的实数根x1,x2,且x1＜1＜x2,求a的取值范围.

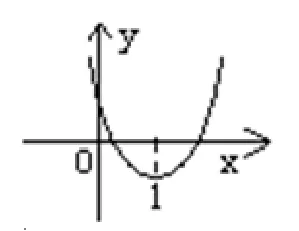
图1

分析由题意可知,a≠0,方程有两个不相等的实数根,Δ=b2-4ac=(a+2)2-4a×9a＞0,若从方程角度寻求解法将涉及多重讨论,解法十分繁琐.不妨借助形象直观的函数图象帮助研究,原方程可变形为x2+x+9=0,则问题等价于y=x2+x+9,建立平面直角坐标系,画出此函数的大致图象如图1,因为1＞0,所以抛物线开口向上,又因为抛物线y=x2+x+9 与x轴交点在(1,0)的两侧,所以当x=1 时,y＜0,12++9＜0,解得-＜a＜0.

本题若从求根公式和根与系数的关系来考虑,方程解法局限性很大,不易获解,把问题转化为二次函数,建立适当的平面直角坐标系,应用坐标方法,借助图象分析形象直观、思路清晰,起到了以简驭繁的最佳效果,问题迎刃而解.可见“形”具有几何的直观性,它也可以表示数之间的某些关系,“形”可以通过逻辑推理得到结果,使推理过程更简捷.

2 函数问题

例2:在高尔夫球争霸赛中,运动员从山坡下点A打出一球向山坡上洞B飞去,已知山坡与水平方向夹角为30°,AB相距18m,球飞行距离为9m 时达到最大高度12m,如图2,球飞行轨迹为抛物线,问能否一杆入洞.

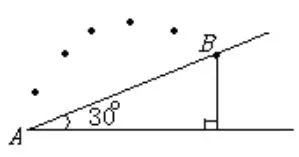
图2

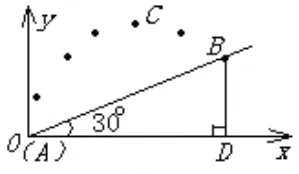
图3

分析这是一个源于实际生活中运动场上的抛物线问题,我们可以把它抽象成数学问题,用解析法解答.建立以A为坐标原点的平面直角坐标系,如图3,此抛物线的顶点为C(9,12)设函数解析式为y=a(x-h)2+k,则y=a(x-9)2+12,把A(0,0) 代入,解得a=所以y=(x-9)2+12,因∠BAD=30°,AB=18m,BD⊥AD,AD=所以B点的坐标是把代入上述函数解析式左边不等于右边,也就是说点B不在抛物线上,故球不能一杆入洞.

本题是有关物体飞行的图象信息问题,题中的数量关系从建立的平面直角坐标系里的图象提供,善于根据图象中的数量关系求出对应的函数关系式,问题得到巧妙解决,体现了坐标方法的奥妙之处.

3 三角问题

例3:如图4,灯塔A周围1000 米水域内有礁石,一舰艇在O处由西向东F方向航行,在O处测得灯塔A在北偏东65°方向上,这时O,A相距4200 米,如果不改变航向,此舰是否有触礁的危险?(供选数据:sin 74°=0.9613,cos 74°=0.2756,tan 74°=3.487)

图4

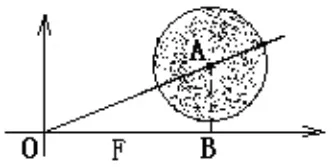
图5

分析结合题意和图形,建立如图5的平面直角坐标系,以O为原点,射线OF为x轴的正半轴,问题转化为求点A到OF的距离与1000 米的大小比较,过点A作AB垂直OF于点B,解RtΔAOB求AB的值即可.

在RtΔAOB中,OA=4200m,∠AOB=90°-74°=16°,AB=OA·sin ∠AOB=4200·sin 16°=4200·cos 74°=4200×0.2756≈1158m＞1000m,可知此舰艇不改变航向,继续前进没有触礁危险.

涉及方向的三角问题,最常用的方法是建立平面直角坐标系,通常选择最重要的“点”尽量是坐标原点,这样将会使问题简化,此题中的“要点”是O点,因此我们应该把这“要点”尽量放在坐标原点,把问题转化为解直角三角形,使问题得以顺利解决.

4 平面几何问题

用坐标方法证明几何问题,首先必须把研究对象置于适合的坐标系中,坐标选择的合适与否对问题的解决有很大的影响.

例4:如图6,在正方形ABCD的AB边上任取一点E,作EF⊥ED,与∠ABC的外角平分线交于点F,求证:EF=ED.

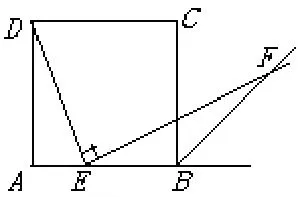
图6

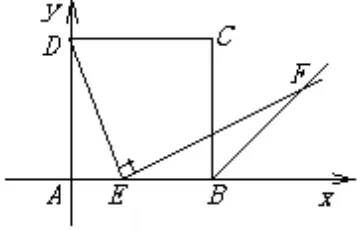
图7

分析建立如图7所示的平面直角坐标系,设A(0,0),B(a,0),E(b,0),∠BEF=β,由三角函数得b=a·tanβ,ED=

直线BF,EF的解析式分别为:y=x-a①

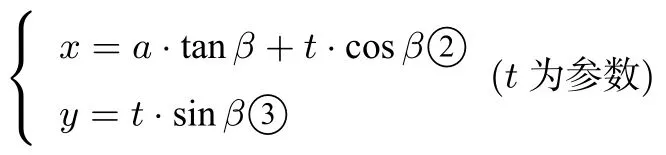
把②,③代入①得t=所以EF=ED.

把直线参数方程中涉及的平面几何最基本元素(点、线、面)常可用来解决与之有关的数量关系,是坐标方法解决平面几何问题最基本的方法策略.

5 不等式问题

例5:当1≤x≤5,求不等式|x2+px+q|≤2 时的p,q值.

图8

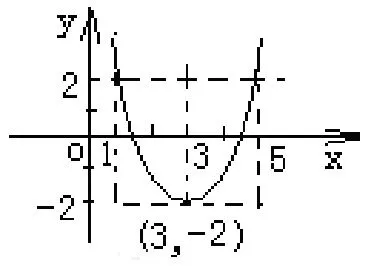
图9

分析对于函数y=x2,当x的值连续增加时,要使函数值的变化幅度不大于4,只能使x从-2 变到2.令y=x2+px+q,建立平面直角坐标系,如图8,因它与y=x2的图象形状相同,位置不同,所以由平移可知,当1 ≤x≤5 时,要使|x2+px+q|≤2,y=x2+px+q的图象只能是图9的情形,此时抛物线的顶点坐标为(3,2).故得解得

本例通过建立平面直角坐标系,借助函数模型,利用坐标方法,巧妙地把图8与图9联系起来考虑,浓缩了观察的数学形式结构,在知识运用上起到了横向联系的效果,体现“形”的几何直观来阐明与“数”之间的关系,利用图形的直观性可简捷地解决问题,从而使问题直观化、简单化,起到了以简驭繁的最佳效果.

6 代数式问题

例6:当x为何值时,代数式-x2+2x+1 的值为正整数,并求出此正整数.

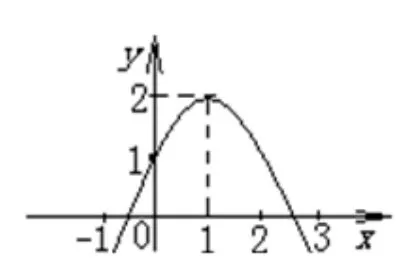
图10

分析这是二次三项式的问题,若把它转换成二次函数模型去考虑,会收到意想不到的解题效果.设y=-x2+2x+1,化简得y=-(x-1)2+2.建立如图10所示的平面直角坐标系,通过二次函数y=-(x-1)2+2 的图象可知函数值域为y≤2,要使-x2+2x+1 的值为正整数,仅且仅当y=1 或y=2.

当y=1 时,即-(x-1)2+2=1,解得x1=2,x2=0;当y=2 时,即-(x-1)2+2=2,解得x1=x2=1.

所以当x=0 或2 时,代数式-x2+2x+1 的值为正整数1;当x=1 时,代数式-x2+2x+1 的值为正整数2.

本题主要以函数作为载体,把二次三项式的问题转化为二次函数问题,应用坐标方法使问题化隐为显,化抽象为形象直观,使学生利于思考问题、分析问题、解决问题.

在教学过程中,我们若借助多媒体和几何画板的演示,在解决数学问题教学中,建立平面直角坐标系,把大量、丰富、复杂的图形用动画演示,可以使学生从不同角度观察,建立空间观念,培养空间想象力和学生的数学应用意识,发展应用数学能力,使问题更直观、简洁,从而有利于分析问题,对提高学生掌握应用坐标方法解决问题能力更有促进作用.值得一提的是,在解题时,要注意坐标方法所独具的解题技巧,否则会使问题变得复杂,使我们陷入繁杂的演算之中.教师给学生传授应用坐标方法解题时,要引导学生根据问题的具体情况,多角度的观察和理解问题,揭示问题的本质联系,利用“数”的准确描述“形”的模糊,用“形”的直观启迪“数”的计算,从而来解决问题.