感受坐标思想 把握坐标内涵
2020-08-10孔凡哲
孔凡哲
数轴是数形结合的典范.平面直角坐标系由两条原点重合且互相垂直的数轴组成,它的发明,使得代数式与图形有机结合在一起,不仅可以使代数问题几何化.而且可以使几何问题代数化.
一维图形就是一条直线.在直线上确定点的位置,必须确定一个基准点和一个基准方向,这个点就是原点,这个方向就是正方向,同时,还要确定度量单位,即单位长度,在确定了原点、正方向和单位长度的直线上,任何一个点都对应着唯一的一个实数,而且仅仅需要一个实数就可以确定点的位置,故数轴上的点和实数是一一对应的,而这个实数就是点的坐标.
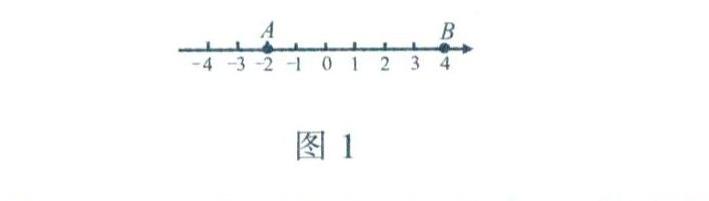
如图1所示,数轴上点A的坐标为-2.若已知某点的坐标是4,则这个点在点B处,
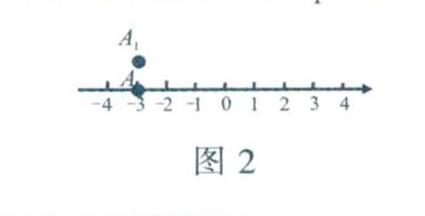
思考1:如图2所示,如果点A的坐标为-3,点A的正上方一个单位长度处有一个点A1,那么该如何表示点A.的位置?
点A1和点A的横向上的位置都是-3,但是纵向上的位置是不同的,相差一个单位长度.利用定位一维图形上的点的方法,无法定位点A1,必须增加新的量才能解决问题.
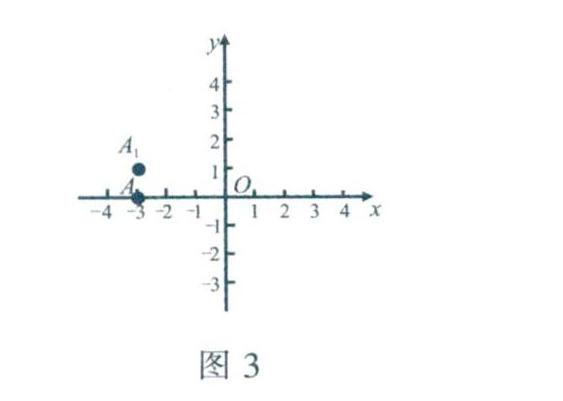
引入纵向轴线,在平面内再画一条与已知数轴垂直,且原点重合的数轴,组成平面直角坐标系.水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,习惯上取向上为正方向;两坐标轴的交点为平面直角坐标系的原点(如图3所示).
点A,的横向上的位置会在x轴上体现,纵向上的位置会在y轴上体现,过点Ai分别向x轴、y轴作垂线,得到了与x轴、y轴相交的两个点(垂足)以及两个点分别对应的实数,我们可以用这个实数对来表示点A,的位置.
因此,点A1的坐标为(-3,1).
在平面内确定一个点的位置,只需要一个数对就可以了,这个数对叫作有序数对.之所以称之为有序数对,是由于数对是一个整体,数对中的两个数有顺序之分,当a≠b时,(a,b)所表示的点与(b,a)所表示的点的位置是不同的,
思考2:若再画一条与已知数轴原点重合、但不垂直的数轴,能否表示点A1的位置?
答案是肯定的,這样的坐标系我们称之为斜坐标系.
当把两条数轴垂直放置时,更方便标记点的位置,因此在实际问题中,我们常常建立适当的平面直角坐标系,根据点的位置写出它的坐标,
如图4,建立平面直角坐标系后,平面上的点可分成两条坐标轴上的点以及四个区域内的点,这四个区域称为象限,右上方的区域称为第一象限,按照逆时针的方向,其他区域依次称为第二、第三和第四象限,两条坐标轴上的点是不属于任何一个象限的.就好比两间房子之间的隔墙是不属于任何一方的,
在平面直角坐标系中,以坐标轴x轴为对称轴,对称点的坐标特点为“横坐标不变,纵坐标互为相反数”;以坐标轴y轴为对称轴,对称点的坐标特点为“纵坐标不变,横坐标互为相反数”.
思考3:若平面内有一点P(a,b),则点P关于坐标原点的对称点P'的坐标是________.
关于坐标原点对称可以分解为先关于x轴对称,再关于y轴对称(或先关于y轴对称,再关于x轴对称).进行两次轴对称变换后的点,与原来的点成中心对称,对称点的坐标特点为“横坐标、纵坐标均互为相反数”,相当于横、纵坐标均乘一1.即点P,的坐标为(-a,-b).
在平面直角坐标系中,将点向左(或向右)平移n个单位长度(n是正数),平移后的点的坐标特点为“纵坐标不变,横坐标减少(或增加)n个单位长度”;将点向上(或向下)平移n个单位长度(n是正数),平移后的点的坐标特点为“横坐标不变,纵坐标增加(或减少)n个单位长度”.
思考4:若平面内的一点沿着某一方向(非坐标轴方向)平移,则平移后的点的坐标应该如何表示?
沿着某一方向(非坐标轴方向)平移,可以分解为先沿着x轴方向平移,再沿着y轴方向平移(或先沿着y轴方向平移,再沿着x轴方向平移),平移后的点的横、纵坐标都会发生相应的变化.
练一练
1.(2019年杭州)在平面直角坐标系中,若点A(m,2)与点B(3,n)关于y轴对称,则(
).
A.m=3,n=2
B.m=-3,n=2
C.m=2,n=3
D.m=-2,n=-3
2.(2019年安顺)在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在(
).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.(2019年广安)若点M(x-l,-3)在第四象限,则x的取值范围是____,
参考答案:
1.B
2.D
3.x>1
