火眼破伪装 金睛显真功

孙伟刚

“平面直角坐标系”的主要学习内容包括确定平面上物体的位置的方法，平面直角坐标系的建立，平面直角坐标系中点的位置与点的坐标之间的相互转化，坐标方法的简单应用等.本章知识既是将数轴（一维直线）内容向平面直角坐标系（二维平面）内容作进一步扩充和延伸，又是今后学习函数图象、方程和不等式的基础，更是用代数方法研究几何问题的基础，其地位举足轻重，为了帮助同学们更好地巩固与提升这部分内容.特整理出典型问题的“伪解法”，供同学们潜心研究，深入思考，火眼破伪装，去粗取精，去伪存真，金睛显真功.

一、概念太模糊，理解想当然

例1如图1.写出平面直角坐标系中点A，B的坐标，

错解：点A的坐标为2.点B的坐标为-3.

【火眼破伪装】本题要求点的坐标，何谓“点的坐标”？其概念表述为：在平面直角坐标系中，任何一点的位置可以用一对有序实数来表示，这样的有序实数对叫作点的坐标.紧抓“点的坐标”的定义，点A、点B钓坐标应该都是用一对有序实数来表示的，因此错解中的解答之所以错误，原因就不言而喻了.

正解：点A的坐标为（2，0），点B的坐标为（0，-3）.

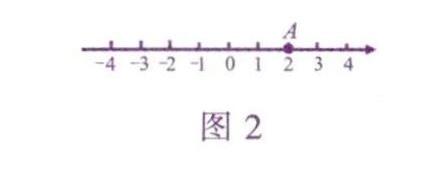
【金睛顯真功】初中数学中有大量的概念，它们是数学知识的重要组成部分，也是导出数学定理和法则的逻辑基础.因此深刻领会数学概念特有的内涵及外延至关重要.理解坐标平面内“点的坐标”这一概念时，要突出“用一对有序实数来表示”这个本质特征，并有意与“如图2.求数轴上点A所对应的实数”这个问题作比较，前者是将点A置于二维平面中，后者则是将点A置于一维直线上，乍看两幅图，点A都对应着实数2，实则不同，前者点A的坐标为（2，0），后者点A对应实数2.如果对“点的坐标”这一概念认识模糊，理解出现偏差，就会出现像错解那样想当然的结果.这是非常可怕的.

二、思维欠严谨，解答不周全

例2在平面直角坐标系中，已知点A的坐标为（2，-1），线段AB//x轴，且AB=3，求点B的坐标.

错解：因为线段AB//x轴，所以点B的纵坐标与点A的纵坐标相同，均为一1.

由于AB=3，故将点A向右平移3个单位长度，即得点B，也就是说，点B的坐标为（5，一1）.

【火眼破伪装】本题还是求点的坐标，也就是求点B的横坐标与纵坐标这对有序实数.由于线段AB∥x轴，根据平行于x轴的直线上的点的坐标特征，故可知点B的纵坐标与点A的纵坐标相同，均为-1，这点毋庸置疑！但如何求点B的横坐标呢？错解中是这样呈现的：由于AB=3，故将点A向右平移3个单位长度，即得点B.平移确实是解决本题的好策略！但平移由方向和距离两个要素来决定，距离倒是已知的，而方向明确吗？难道只能向右平移3个单位长度吗？向左平移3个单位长度行不行呢？在一连串的问题中，思维的缜密性得到了锻炼，问题的“伪解法”终被火眼识破.

正解：因为线段AB//x轴，所以点B的纵坐标与点A的纵坐标相同，均为-1.

由于AB=3，故将点A向左平移3个单位长度或向右平移3个单位长度，均可得到点B.

如图3所示，若将点A向右平移3个单位长度，则得点B的坐标为（5，-1）.

若将点A向左平移3个单位长度，则得点B'的坐标为（-1，一1）.

因此点B的坐标为（5，一1）或（-1，一1）.

【金睛显真功】数学思维的严谨性是指研究问题时要严格遵守逻辑规则，做到概念清晰、判断正确、推理有据，它反映了思维活动中的严谨和缜密程度.而知识储备不足、审题能力薄弱、解题习惯不好等都是造成考虑问题不周全的重要原因.因此，我们要牢记“平移由方向和距离两个要素来决定”这个知识，要能将问题退化为如下的源头问题作思考：点A是一条直线上的定点，试在这条直线上画线段AB=3，会出现哪几种情况？（必要时可以画出图形直观感知，如图4所示）要能在解题完毕后养成检验反思的好习惯……如果我们做到了，那么再美的“伪装”终将被“打回原形”.

练一练

1.若坐标平面内点A（m，n）在第四象限，则点B（n，m）在（

）.

A.第一象限

B.第二象限

C.第三象限

D.第四象限

2.若点P（m+3，m+1）在x轴上，则点P的坐标为（

）.

A.（0，-2）

B.（2，0）

C.（4，0）

D.（0，-4）

3.若点P（x，y）在第二象限，且|x|=2，|y|=3，则点P的坐标是____.

4.在平面直角坐标系内，若将点A（-2，3）向右平移3个单位长度到点B，则点B的坐标是一.

5.如图5，点A （-1，0），C（1，4），点B在x轴上，且AB=3.

（1）求点B的坐标，并画出△ABC.

（2）求△ABC的面积.

参考答案：

1.B 2.B 3.（-2，3） 4.（1，3）5.（1）（2，0）或（-4.0），图略. （2）△ABC的面积为6.