二面角视角下多面体外接球的探究
2020-08-10福建省厦门市湖里中学361006
福建省厦门市湖里中学(361006) 严 杜
广东省广州市荔湾区教育发展研究院(510370) 庞新军
近年来求多面体外接球的问题在高考试卷和各地模拟卷中频频出现,解决多面体外接球的方法主要依靠构造长方体模型来求解,有较大的局限性.笔者注意到在求多面体外接球中已融入“二面角”的现象,本文从两道求多面体外接球的问题出发,以“二面角”的视角来进行多面体外接球的探究.
一、问题提出
题1(2013年高考全国卷理科第16 题)如图1,已知圆O和圆K是球O的大圆和小圆,其公共弦长等于球O的半径,且圆O与圆K所在的平面所成的一个二面角为60◦,则球O的表面积等于____.(答案:16π.)
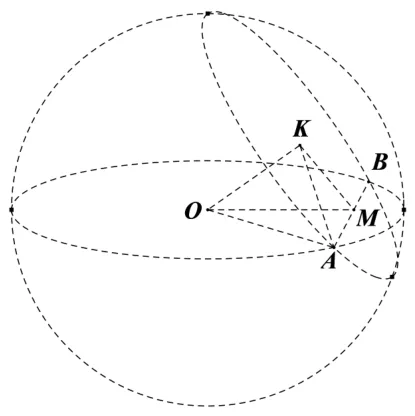
图1
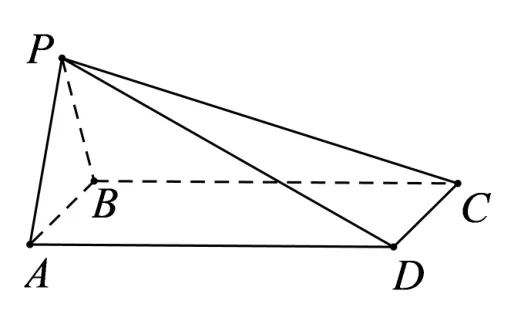
图2
题2如图2,已知四棱锥P−ABCD的顶点都在球O的球面上,底面ABCD是矩形,平面PAB ⊥平面ABCD,∆PAB为正三角形,AD=2,AB=4,则球O的表面积为____.(答案:.)
题1 中两个截面圆所在平面所成二面角为60◦,题2 中平面PAB⊥平面ABCD,即两个平面所成二面角为90◦,二者同为特殊角,求解方法是否有通法可循? 笔者接下来对上述两题的立体几何图形背景进行深入分析,结合二者的特点从特殊到一般展开探究.
二、二面角为90◦的多面体外接球探究
探究1在球内接多面体中,存在两个不同的相交面互相垂直,且分别在球O的截面圆O1、O2上,两截面圆的半径分别为r1、r2,两相交面的公共弦为AB,弦长为2l,求球O的半径R.
解析如图3,M为公共弦AB中点,则在Rt∆AMO1和Rt∆AMO2中,可知两圆的弦心距有MO12=r21−l2,MO22=r22−l2.又圆O1所在平面与圆O2所在平面垂直,有∠O1MO2=90◦,因此平面四边形OO1MO2为矩形,则外接球的弦心距有:MO2=MO12+MO22.在Rt∆AMO中,OA2=MO2+l2.综上所述,球O的半径有:
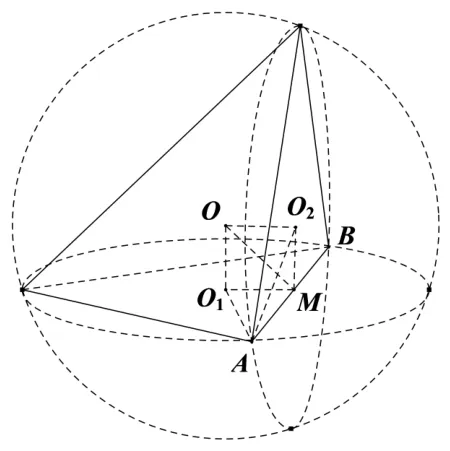
图3
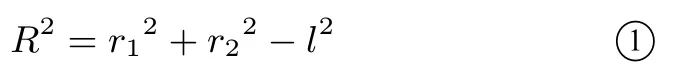
通过探究1 找到了存在两相交面垂直的多面体的外接球的求解策略,即找到了存在两相交面的二面角为90◦的多面体的外接球的求解策略,那类比题1,若多面体存在两相交面的二面角为60◦,其外接球求解策略是否有通法?
三、二面角为60◦的多面体外接球探究
探究2在球内接多面体中,存在两个不同的相交面,分别在多面体外接球O的截面圆O1、O2上,两截面圆的半径分别为r1、r2,两相交面的二面角为60◦,公共弦为AB,弦长为2l,求球O的半径R.
解析如图4,两圆的弦心距有MO12=r21−l2,MO22=r22−l2,两相交面的二面角为60◦,即其平面角∠O1MO2=60◦.在∆MO1O2中,由余弦定理知两圆的圆心距有,O1O22=MO12+MO22−MO1·MO2.如图5,在平面四边形OO1MO2中,由OO1⊥MO1,OO2⊥MO2得,MO为四边形OO1MO2外接圆的直径,由正弦定理知外接球的弦心距有:在Rt∆AMO中,OA2=MO2+l2.综上所述,球O的半径有:
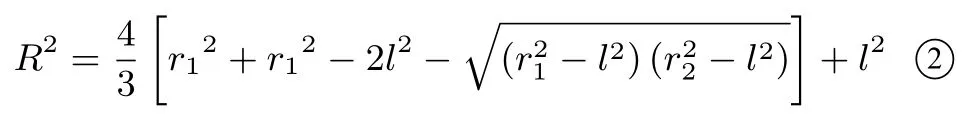
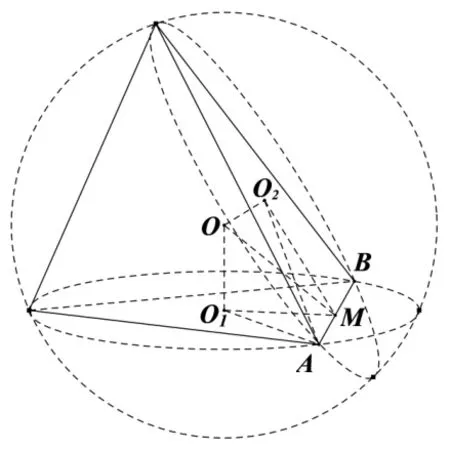
图4
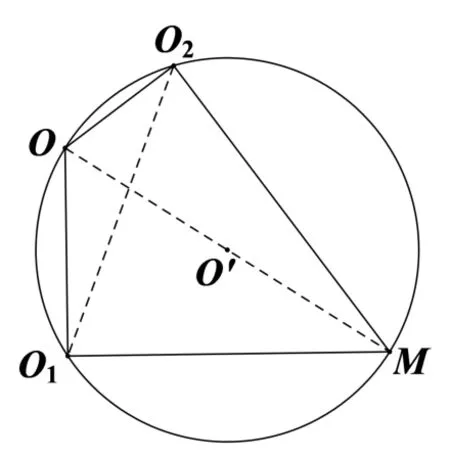
图5
笔者发现通过探究存在两相交面的二面角为60◦的多面体的外接球的求解策略,“二面角”视角下的外接球求解策略越来越趋于明朗化,因此接下来将对“二面角”视角进行拓宽,并将外接球求解策略规范步骤化.
四、任意二面角的多面体外接球探究
探究3在球内接多面体中,存在两个不同的相交面,分别在多面体外接球O的截面圆O1、O2上,两截面圆的半径分别为r1、r2,两相交面的二面角为α,公共弦为AB,弦长为2l,求球O的半径R.
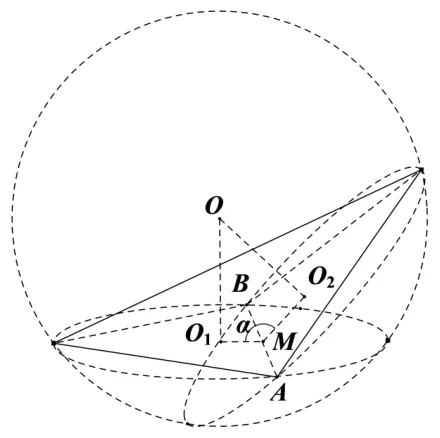
图6
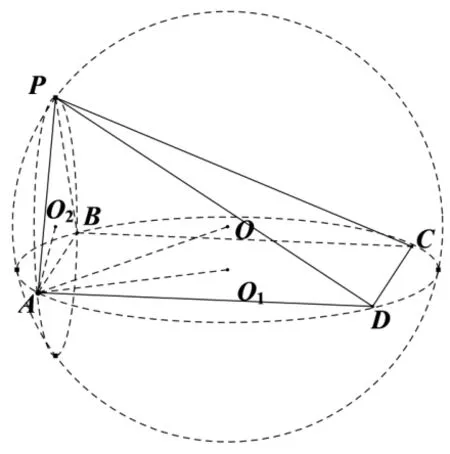
图7
解析如图6,按照探究2 的解析,依次求出两圆的弦心距、圆心距以及外接球的弦心距最终求得外接球半径,两圆O1、O2的弦心距:MO12=r21−l2,MO22=r22−l2;两圆O1、O2的圆心距:O1O22=MO21+MO22−2MO1·MO2·cosα;外接球O的弦心距:外接球O的半径R:由OA2=MO2+l2得:
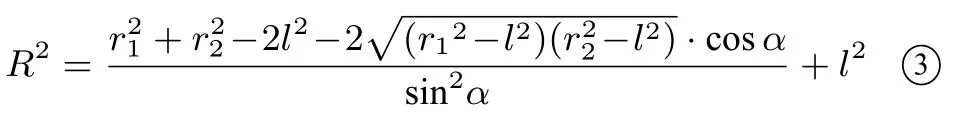
上述解析将“二面角”视角下的外接球求解策略变得更加明了,即使对于空间想象能力不足的学生,如果能熟练掌握上述结论,在高考中就会得到事半功倍的效果.
五、含二面角的多面体外接球实例运用
例1同题2
解析如图7,按照外接球求解策略得解答如下:矩形ABCD的外接圆圆O1的半径:∆PAB外接圆O2的半径:由探究结论知外接球O的半径:故外接球O的表面积:
评注本题还可以采用构造外接圆柱或者外接圆台[1]来求解外接球,这里是其第三种解决策略,不同的视角去看待外接球问题展示出不同的解题策略.
例2(2018年佛山一模理科第16 题)平面四边形ABCD中,沿直线AC将∆ACD翻折成∆ACD′,当三棱锥D′−ABC的体积取得最大值时,该三棱锥的外接球表面积为____.
解析如图8,要使三棱锥D′−ABC的体积取得最大值,就是使平面ACD′⊥平面ABC,也就是使这两个平面的二面角为90◦,设外接球半径为R,公共弦2l=4,因此由外接球求解策略解答如下:
评注本题的难点在于利用正、余弦定理求出两小圆半径,在求三角形外接圆半径时,正、余弦定理是一种常用的方法.
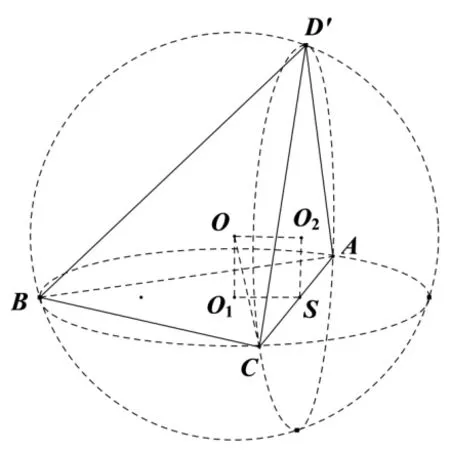
图8
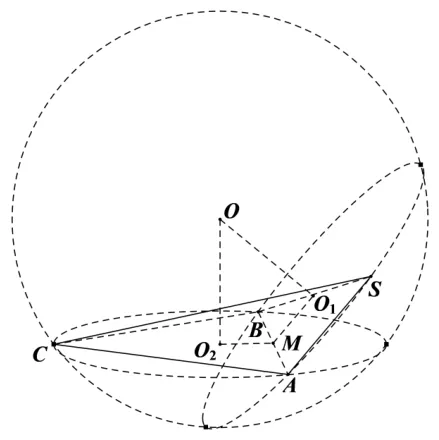
图9
例3(2017年福建单科质检理科第16 题)在三棱锥S−ABC中,∆ABC是边长为3 的等边三角形,二面角S−AB−C的大小为120◦,则此三棱锥的外接球的表面积为_____.
解析如图9,知公共弦AB=2l=3,圆O1、O2的半径:∆ABC为等边三角形,则由SB2=SA2+AB2知∆SAB为直角三角形,则外接球O的半径:
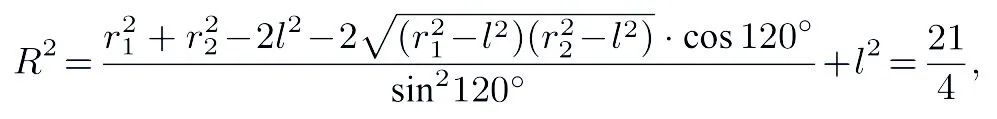
故外接球O的表面积:S=4πR2=21π.
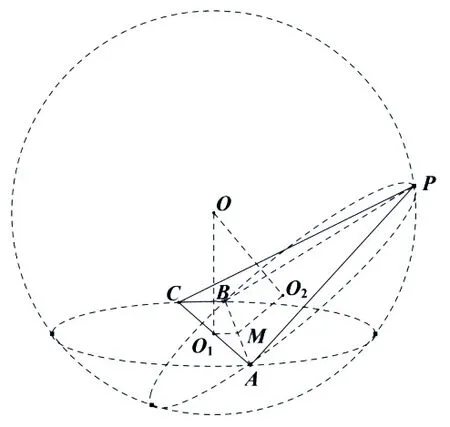
图10
评注由圆O1与O2的半径相等知二者是大小相等的两个小圆,因此,若多面体两相交侧面的外接圆半径相等,即r1=r2=r,其外接球半径为:
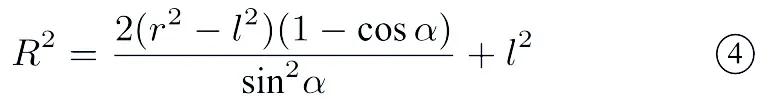
例4已知三棱锥P−ABC中,AB⊥BC,且二面角P−AB−C的大小为150◦,则三棱锥P−ABC外接球的表面积为( ).
A.100πB.108πC.110πD.111π
解析如图10,按照外接球求解策略得解答如下:
圆O1的半径:∆ABC为直角三角形,则圆O2的半径:先后利用余弦、正弦定理求得外接球O的半径:
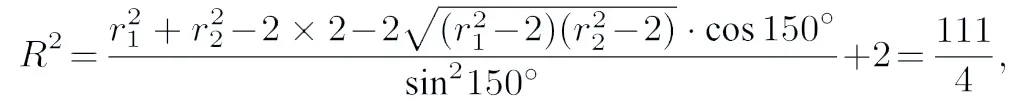
故外接球O的表面积:S=4πR2=111π,故选D.
评注本题如果按照往常的解题方法先找球心,无疑是给缺乏空间想象能力的学生设置了一道拦路虎,而按照本文的解题策略只需要找出相关数据进行计算即可得出答案.本题的难点在于计算量大.
本文受题1 与题2 启发,将题目中若隐若现的“二面角”元素提取出来,从特殊到一般循序渐进的研究了多面体外接球求解策略.经过三个探究从特殊二面角到任意二面角,逐步明晰解决这一类问题的步骤.通过对试题深入的分析探究,挖掘试题的特征,揭露试题的本质,帮助学生总结通性通法,有助于提高学生分析和解决问题的能力,提高学生的创造精神.
