考虑剪切效应的金属本构关系模型及其在大型筒节轧制成形中的应用①
2020-07-24焦云静董志奎孙建亮赵静一卢明立
焦云静, 董志奎,, 孙建亮,3, 赵静一, 卢明立
(1.燕山大学 机械工程学院,河北 秦皇岛066004; 2.江苏天明机械集团有限公司,江苏 连云港2220022; 3.燕山大学 国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛066004)
大型筒节类零件广泛应用于核电、石化、航空航天领域,其外径可达8 m,宽度达2~3 m,厚度达0.3 m[1]。在大型筒节轧制过程中,轧制力的控制具有重要作用,其中变形抗力作为轧制工艺设计的最基本参数之一,是研究重点。 目前对变形抗力的研究主要集中于压缩行为,但在筒节轧制过程中,由于轧制变形区中存在受到压剪作用的搓轧区[2],因此要进行压剪行为的研究,以进一步分析筒节的轧制过程并预测轧制力。
张博[3]进行了2.25Cr1Mo0.25V 钢的压缩行为研究并建立了变形抗力模型;李科元[4]研究了40Cr 钢的热变形特征并建立了变形抗力模型。 但上述研究均为单一压缩行为研究,所得变形抗力模型不包含剪切效应的作用。 国内外主要有2 种方式来模拟剪切效应,一是利用霍普金森压剪杆[5],二是通过设计实验试件。 但目前主要应用于岩土材料的剪切变形方面[6-7],关于金属的研究比较少。 Rittle[8]设计了SCS试样以实现剪切效应,并利用有限元软件证明,在常温下该试件可以达到更大的应变速率和应变程度[9-10];桑德利[11]研究了高温下金属的压剪变形,但选用模型为尺寸单一的难变形材料,不适用于本文所研究的内容。 孙建亮[12]等建立了一种基于条块法的筒节轧制力计算模型,将计算结果和工厂结果进行对比,证明了模型的精度。 但其在计算剪切应力时采用了经验公式,导致最终的轧制力计算结果与实测结果偏差较大。为进一步提高大型筒节轧制力计算结果的精度,本文建立了考虑剪切效应的变形抗力模型,并将其应用到大型筒节轧制力计算,实现轧制力的预报。
1 实验研究
1.1 实验方案
试件材质为2.25Cr⁃1Mo⁃0.25V 钢,其化学成分如表1 所示。

表1 2.25Cr⁃1Mo⁃0.25V 钢化学成分(质量分数)/%
图1 为普通圆柱形试件示意图;图2 为SCS 压剪试件示意图。 试件尺寸均为Φ10 mm × 20 mm, 上下圆形端面精车,其端面仅承受压力P。 在SCS 压剪试件中,与圆柱体的纵向轴线呈45°的方向上加工两条斜槽,使得剪切带承受压剪复合作用。 剪切带的尺寸由槽的宽度(w)和厚度(t)决定,t=2.5 mm,w=0.25,0.50,1.00,2.00 mm。

图1 普通圆柱试件示意

图2 SCS 压剪试件示意图(单位:mm)
本次实验采用开槽试件作为主分析模型,普通圆柱试件作为对比模型,主要对比分析试件在承受压剪复合作用和压缩作用下的变形特征。 实验升温、降温方案如图3 所示。 以10 ℃/s 的速度将试件加热至1 200 ℃并保温5 min,之后以5 ℃/s 的速度将试件温度降至1 000 ℃并保温2 min,最后分别以0.01,0.1,1.0 s-1的变形速率进行压缩,压缩变形量为20%。 由于Gleeble⁃3800 试验模拟机采集的参数为电脑按照圆柱的计算方程自动给出,不适用于SCS 压剪试件,故首先对相关参数进行处理。
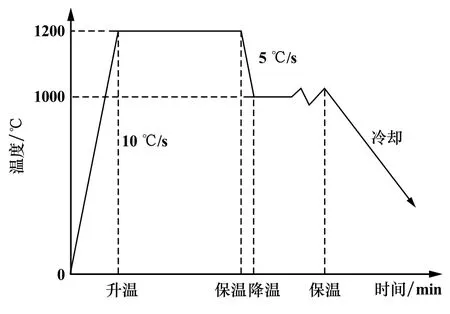
图3 实验升温、降温方案
1.2 实验结果分析与讨论
首先绘制SCS 压剪试件的压力(P)⁃位移(d)曲线,并与普通圆柱试件作对比,如图4 所示。
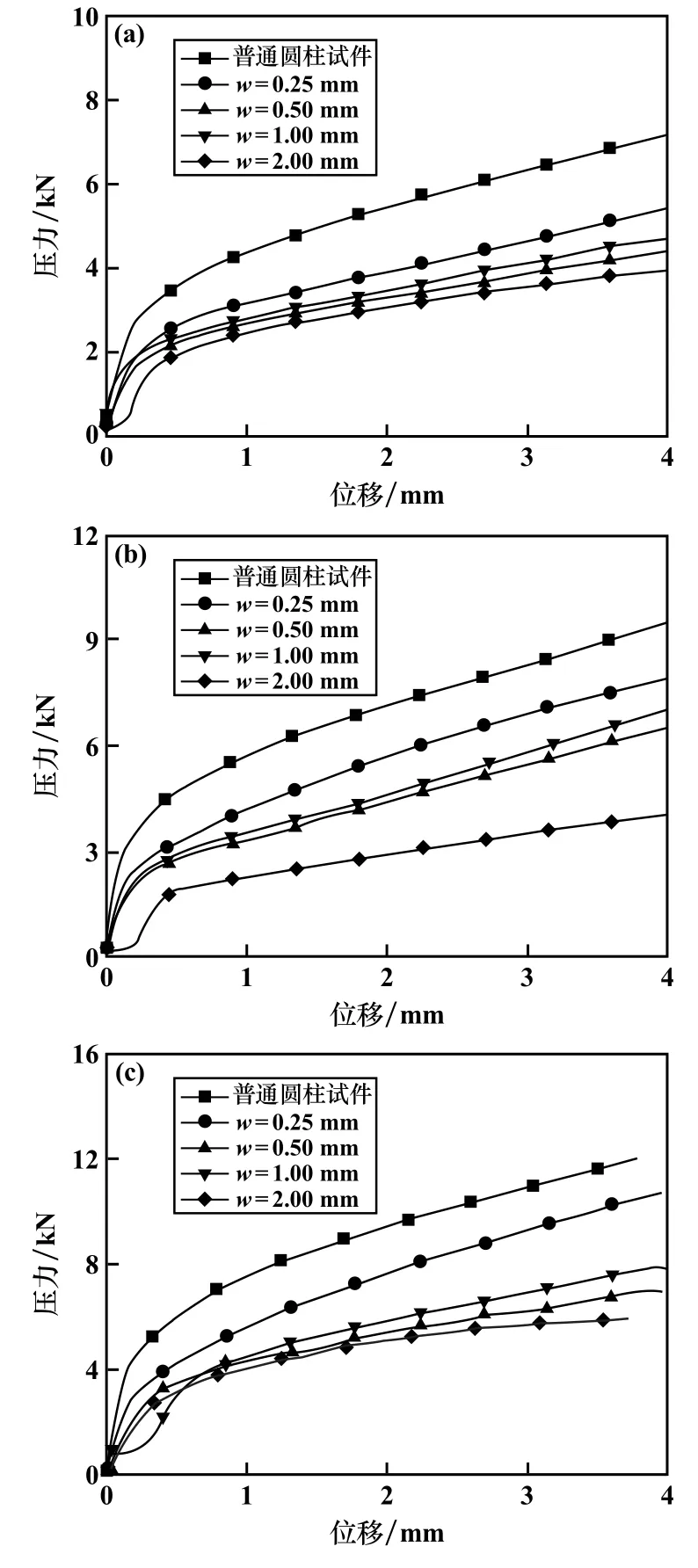
图4 压力⁃位移曲线对比图
已知SCS 压剪试件中剪切带承受压剪复合作用,主要变形为剪切变形。 由图4 可得:
1) 在不同应变速率下,普通圆柱试件受到的压力最大,随着开槽宽度w逐渐增加,SCS 压剪试件受到的压力逐渐减小。
2) 当槽宽w=0.50 mm 时,SCS 压剪试件的合力略小于槽宽w=1.00 mm 时的合力,这是由于SCS 压剪试件中剪切变形的存在使得剪切力随开槽宽度增加逐渐增大,以补偿逐渐减小的压力,从而剪切带中压力和剪切力的复合作用使得后者受到的合力略大于前者。
根据式(1)~(2)将P⁃d(压力⁃位移)关系进行转化[9-10](D为试件直径),得到SCS 压剪试件的应力和应变数据,将SCS 压剪试件的应力⁃应变关系和普通圆柱试件的应力⁃应变关系进行对比,结果如图5 所示。
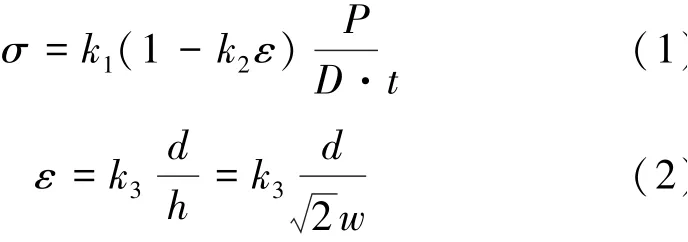
式中k1、k2、k3分别为相关回归系数。

图5 普通圆柱试件和SCS 压剪试件应力⁃应变曲线对比图
由图5 可知:
1) 在一定的应变速率下,随着金属应变程度增加,应力逐渐增加,当变形程度达到一定值后,应力的增大趋势减缓。
2) 在变形温度和变形速率不变的前提下,随金属应变程度增加,槽宽w越大,SCS 压剪试件的应力越小。
3) 在同等条件下,与普通圆柱试件相比,SCS 压剪试件能够达到更大的应变。
4) 在变形温度和应变程度不变的前提下,变形抗力随应变速率升高而升高。
通过分析,得到筒节材料的变形抗力模型:
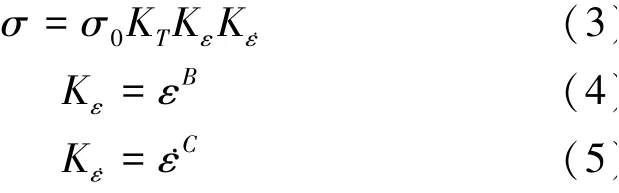
式中σ0为一定变形条件下的应力,MPa;KT为与变形温度相关的系数;Kε为与变形程度相关的系数;K̇ε为与变形速率相关的系数;B、C分别为与金属材料相关的系数。
因为本文主要研究剪切变形对金属变形抗力的影响,因此将温度对变形抗力影响系数暂设为1,对应力⁃应变曲线进行回归,得到其变形抗力数学模型如表2 所示。
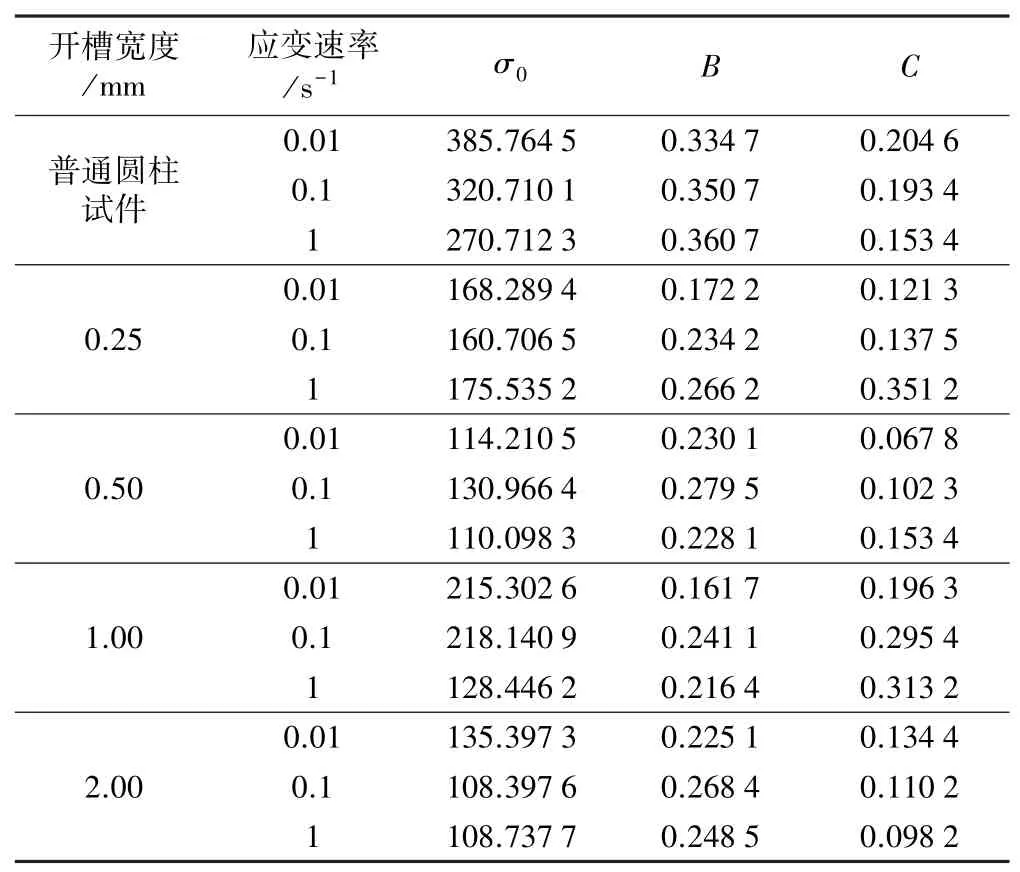
表2 筒节材料2.25Cr⁃1Mo⁃0.25V 合金钢的变形抗力数学模型
2 考虑剪切效应的轧制力分析
2.1 筒节轧制力理论计算模型
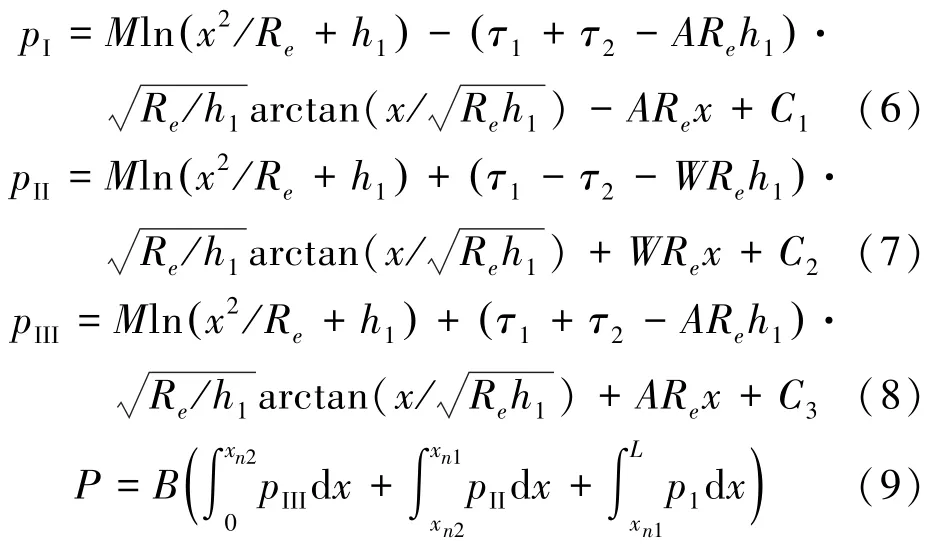
筒节轧制力的理论计算采用如下模型[13]:式中pI,pII,pIII分别为筒节轧制过程中后滑区、搓轧区、前滑区的单位轧制力,MPa;B为筒节宽度,mm;P为筒节轧制总轧制力,N。
上述的轧制力数学模型中剪切应力计算采用如式(10)的经验公式,而本文中τ 的计算采用前文中建立的数学模型。

式中m为摩擦因数;k为筒节轧制接触表面的剪切变形抗力
本文采用的大型筒节轧制工艺参数如表3 所示。
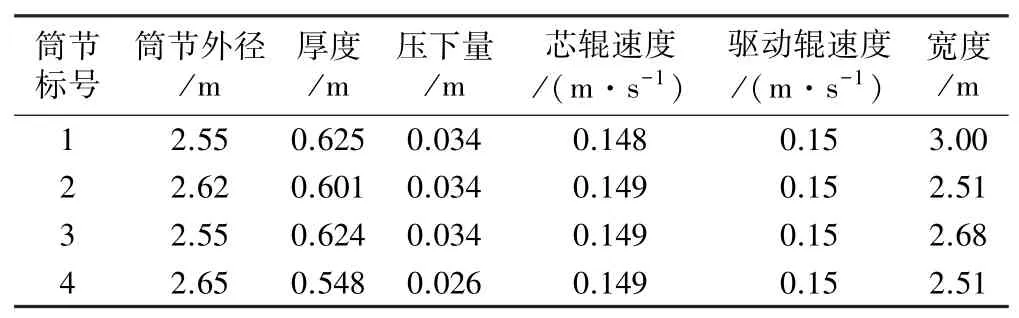
表3 轧制工艺参数
大型筒节应变速率和应变程度采用下式计算:
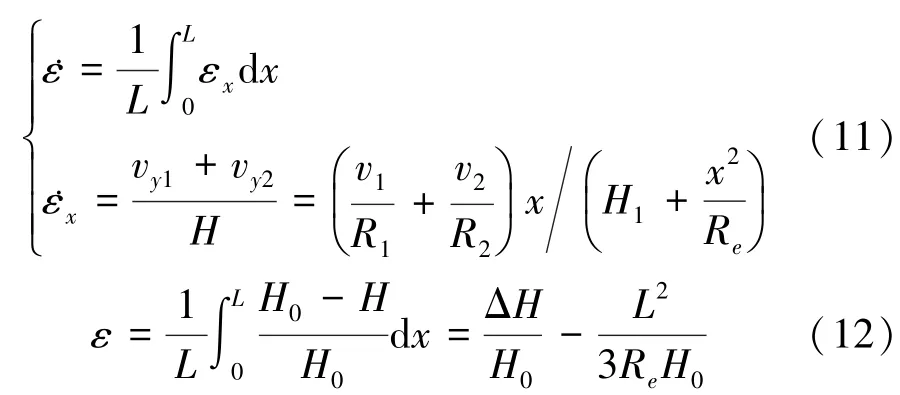
式中具体参数含义参照文献[13]。
2.2 筒节轧制有限元模型
按照表3 所示的大型筒节实际轧制工艺参数,采用ABAQUS 有限元软件建立大型筒节轧制三维刚塑性有限元模型,如图6 所示。

图6 筒节轧制三维刚塑性有限元模型
模型具有如下主要特征:将驱动辊和芯辊设置为刚体,驱动辊和芯辊均围绕自身轴线转动,筒节设置为刚塑性体,利用Python 语言自定义设置筒节的本构关系模型,以符合前文建立的复杂变形状态;轧辊与轧件之间的摩擦为库伦摩擦类型,驱动辊和芯辊与筒节内外表面摩擦因数设定为0.5;定义工件的初始温度为1 000 ℃,轧辊的温度均设定为30 ℃,环境温度为30 ℃。筒节与轧辊的接触换热系数设定为10 N/(s·mm·℃),热辐射系数设定为0.8 N/(s·mm·℃),塑性变形中功热转化系数设定为0.9。
2.3 大型筒节轧制力计算结果分析
以往的学者在计算轧制力的时候使用剪切应力τ的经验公式,而非考虑剪切变形的数学模型,由此得到筒节的理论计算轧制力[2],本文中通过建立的考虑剪切效应的数学模型来计算轧制力,本文模型、不考虑剪切效应的模型和工厂实测轧制力及有限元结果对比如表4 所示。
由表4 可知:
1) 采用本文建立的变形抗力模型计算轧制变形区的剪切力,所得结果与工厂实测轧制力相对误差更小,相对误差在8%以内,相对其他方法精度更高。
2) 有限元模型计算的轧制力与工厂实测轧制力相比,相对误差在范围要求内,本文建立的模型在有限元层面得到验证。
上述分析说明理论计算筒节轧制力时,筒节轧制变形区中的剪切效应不容忽视,应用考虑剪切效应的变形抗力模型可以提高筒节轧制力的计算精度。
3 结 论
1) 设计了不同的SCS 压剪试件,基于SCS 压剪试件的实验数据得到了SCS 压剪试件的应力应变数据,从而建立了考虑剪切效应的金属塑性变形抗力数学模型,并与普通圆柱试件结果进行对比,发现在相同的变形条件下,SCS 压剪试件受到的变形抗力更小;随着槽宽逐渐增加,SCS 压剪试件受到的压力和变形抗力逐渐减小。
2) 将建立的考虑剪切效应的变形抗力模型应用到筒节轧制中,理论计算轧制力和实测轧制力结果吻合,相对误差在8%以内,与以往采用经验公式计算的筒节轧制力相比,应用考虑剪切效应的模型达到的精度更高。
3) 建立了筒节轧制过程的三维热力耦合有限元模型,将有限元计算的轧制力与理论计算轧制力、工厂实测轧制力进行对比,得到的相对误差同样满足要求。
