迁移、应用问题

一、填空题

1.（2020年石家庄市模拟卷）将边长为1m的正三角形薄铁皮沿一条平行于某边的直线剪成两块，其中一块是梯形，记s=，则s的最小值是________.

2.将一个长、宽分别是a，b（0＜b＜a）的铁皮的四个角切去相同的正方形，然后折成一个无盖的长方体盒子，若这个长方体的外接球的体积存在最小值，则的取值范围是________________.

3.江苏省南京地区的一种机动车牌号由两部分组成，一是固定部分：苏A；二是随机部分：三个阿拉伯数字（0，1，2，…，9）和两个大写的英文字母（A，B，C，…，Z），且按三个数字相邻，两个字母紧随其后的方式排列，如“苏A·866GQ”，则这种类型的车牌号理论上最多有________个.

4.如图所示，垂直于地平面竖立着一块半圆形的木板，某时太阳的光线恰与半圆的直径AB垂直，此时木板在地面上的投影是半椭圆，已知半椭圆投影的面积与半圆木板的面积之比等于，则光线与地面所成角的大小为________.（注：长轴长为2a，短轴长为2b的椭圆面积S=πab）.

（第4题）

5.（2020年镇江市模拟卷）已知A，B，C是平面上任意三点，BC=a，CA=b，AB=c，则的最小值为________.

6.在集合｛1，2，3，…，9｝的所有3元子集中，将每个子集中最小元素相加，和记为a；将每个子集中最大元素相加，和记为b；将每个子集中中间元素相加，和记为c，则a：b：c为________.

二、解答题

8.某企业拟生产一种如图所示的圆柱形易拉罐（上下底面及侧面的厚度不计），易拉罐的体积为108πmL.设圆柱的高度为hcm，底面半径为rcm，且h≥4r.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为m元/cm2，易拉罐上下底面的制造费用均为n元/cm2（m，n为常数）.

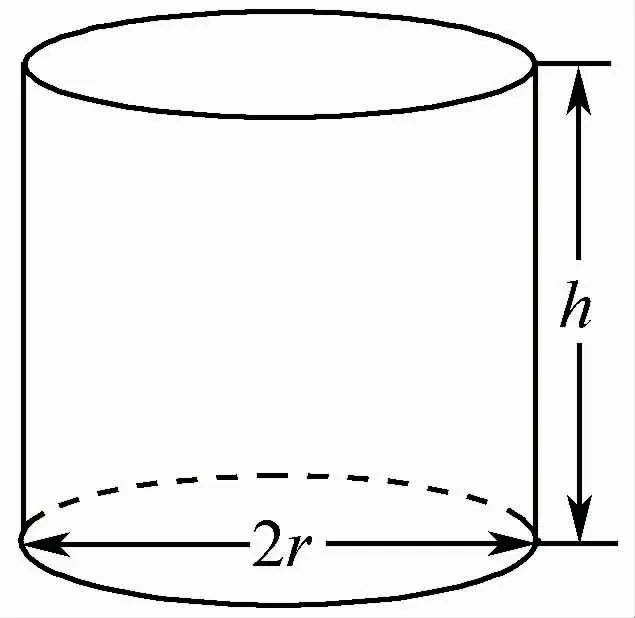
（第8题）

（1）写出易拉罐的制造费用y（元）关于r（cm）的函数表达式，并求其定义域；

（2）求易拉罐制造费用最低时r（cm）的值.

9.（2020年苏州中学模拟卷）如图所示，有一块边长为1km 的正方形区域ABCD，在点A处有一个可转动的探照灯，其照射角（∠PAQ）始终为45°（其中点P，Q分别在边BC，CD上），设∠PAB=θ，tanθ=t.

（1）用t表示PQ的长度；

（2）求探照灯照射在正方形ABCD内部区域的面积S的最大值.

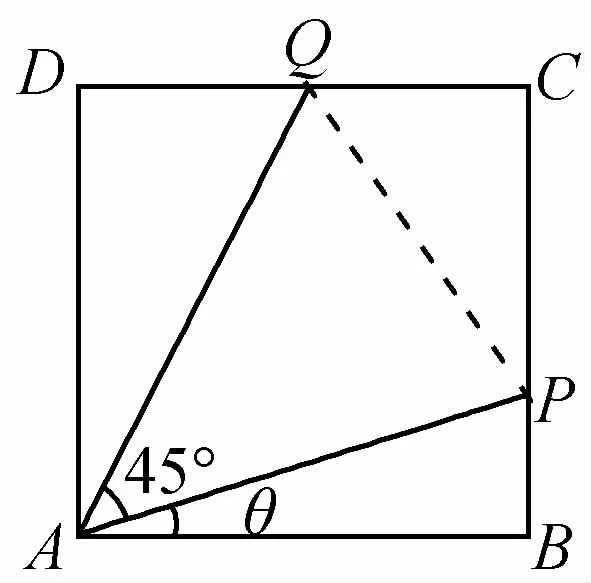
（第9题）

10.如图，GH是东西方向的公路北侧的边缘线，某公司准备在GH上的一点B的正北方向的A处建一仓库，设AB=ykm，并在公路同侧建造边长为xkm的正方形无顶中转站CDEF（其中边EF在GH上），现从仓库A向GH和中转站分别修两条道路AB，AC，已知AB=AC+1，且∠ABC=60°.

（1）求y关于x的函数解析式；

（2）如果中转站四周围墙造价为1万元/km，两条道路造价为3万元/km，问：x取何值时，该公司建中转站围墙和两条道路总造价M最低？

11.以（0，m）间的整数（m＞1，m∈N）为分子，以m为分母组成分数集合A1，其所有元素和为a1；以（0，m2）中的整数为分子，以m2为分母组成不属于集合A1的分数集A2，其所有元素和为a2；…；以此类推，以（0，mn）（n∈N*）中的整数为分子，以mn为分母组成不属于集合A1，A2，…，An-1的分数集An，其所有元素和为an.求：

（1）a1，a2，a3的值；

（2）｛an｝的通项公式；

（3）a1+a2+…+an.