立体几何问题的正确打开方式：“算”与“思”（下）

曾 荣

传统“作—证—算”，重在思维，多思少算

例1（2019年高考全国I 理科卷）如图，直四棱柱的底面是菱形，E，M，N分别是BC，BB1，A1D的中点．

（1）证明：MN∥平面C1DE；

（2）求二面角A-MA1-N的正弦值．

上期我们已经对例1 作了分析，本期继续对第（2）问探索．

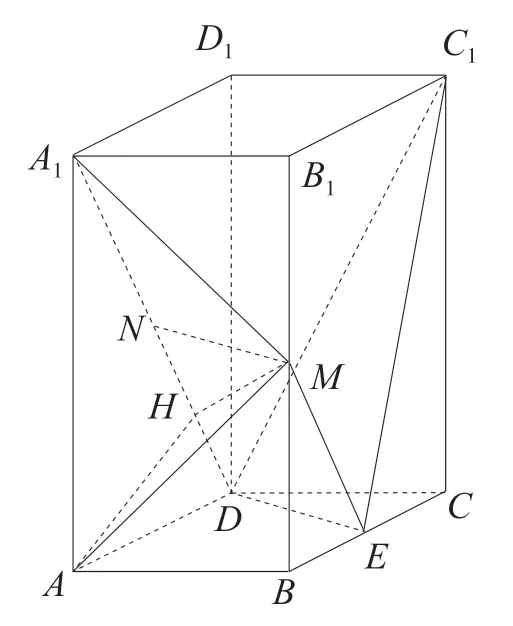
图1

【思路剖析】（综合几何法，利用三垂线定理先作出二面角的平面角，再进行计算）

过点A作AH⊥A1D，垂足为H，连结MH．

因为底面是菱形，∠BAD=60°，所以△BCD为等边三角形，

因为E是BC的中点，所以DE⊥BC，所以DE⊥DA．

又AD，D1D⊂平面ADD1A1，AD∩D1D=D，

所以DE⊥平面ADD1A1，所以DE⊥AH．

又DE，A1D⊂平面A1DEM，DE∩A1D=D，所以AH⊥平面A1DEM．

所以AH⊥A1M，又AM⊥A1M，AH∩AM=A，所以A1M⊥平面AMH，所以MH⊥A1M，所以∠AMH为二面角A-MA1-N的平面角．

在Rt△A1AD中，因为AH⊥A1D，所以AH·A1D=AA1·AD，求得．

所以二面角A-MA1-N的正弦值为．

敲黑板

这里采用传统“作—证—算”的综合几何法求解，“作”后要进行严谨的“证”．此法运算量明显小于向量坐标法．

例2（2018年高考全国I 文科卷第18题）如图，在平行四边形ABCM中，AB AC==3，∠ACM=°90，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA．

（1）证明：平面ACD⊥平面ABC；

（2）Q为线段AD上一点，P为线段BC上一点，且，求三棱锥Q-ABP的体积．

图2

【思路剖析】

本题是以折叠为背景的几何问题，研究此类问题，我们要理清图形变换前后在数量关系和位置关系上的不变性：

显性变换：以AC为折痕将△ACM折起，使点M到达点D的位置数量关系的不变性DC CM=，AD AM=位置关系的不变性CA CM⊥，CA CD⊥，CA AB⊥隐性 △ ≌△CAMCAD可求得AD BC==3 2，BD=3 3，可证得CD BC⊥可结合AB DA⊥ 证得AB⊥平面CAD，CD⊥平面ABC

第一问思路：证平面ACD⊥平面ABC的大方向是证线面垂直．通常的方法有：

思路①通过证明AB⊥平面ACD来证平面ACD⊥平面ABC；

思路②通过证明CD⊥平面ABC来证平面ACD⊥平面ABC．

第二问思路：

思路①直接作图法，分别求出底面积和高，利用体积公式计算；

思路②利用体积转换法，将求不规则几何体的体积转化为求规则几何体的体积．

【规范解答】

（1）证法一（通过证明AB⊥平面ACD来证平面ACD⊥平面ABC）：

因为四边形ABCM是平行四边形，CM⊥AC，所以AB⊥AC．

又BA⊥AD，AC，AD⊂平面ACD，AC∩AD=D，所以AB⊥平面ACD．

又AB⊂平面ABC，所以平面ACD⊥平面ABC．

证法二（通过证明CD⊥平面ABC来证平面ACD⊥平面ABC）：

连结BD．

在Rt△ACD中，DC=AC=3，所以．

在Rt△ABC中，AB=AC=3，所以．

在Rt△ABD中，，AB=3，所以．

在△BCD中，，所以．所以CD⊥BC．

又CD⊥AC，AC，BC⊂平面ABC，AC∩BC=C，所以CD⊥平面ABC．

又CD⊂平面ACD，所以平面ACD⊥平面ABC．

（2）解法1（直接作图法）

过点Q作QE⊥AC，垂足为E，则QE∥CD．

解法2（体积转换法）

设三棱锥Q-ABP的高为h，因为，所以故．

图3

【归纳提升】

（1）研究线面位置关系问题，同学们要熟练掌握以下关系：

（2）求体积问题时，同学们要善于利用体积之比，将求不规则几何体的体积转化为求规则几何体的体积，即将一个高和底面积不易求的几何体，转化为高和底面积都容易计算的几何体．善于转化，可使问题越变越简单．

解决立体几何证明和计算问题，需要同学们根据自己的学习基础，灵活地选用综合几何法和向量坐标法．但无论采用哪种方法，都需要遵循“解而优则选”的原则，多思少算，达到事半功倍的效果．

（“小试牛刀”见第48 页）