本期“小试牛刀”合集

一、计数原理（上接第12页）

1．安排3 名志愿者完成4 项工作，每人至少完成1 项，每项工作由1 人完成，则不同的安排方式共有___________________种．

2．满足a,b∈(-1,0,1,2)，且关于x的方程ax2+2x+b=0 有实数解的有序数对（a，b）的个数为________．

3．将一个四面体ABCD的六条棱涂上红、黄、白三种颜色，要求共端点的棱不能涂相同颜色，则不同的涂色方案有________种．

4．如果一个三位正整数如“a1a2a3”满足a1a3，则称这样的三位数为凸数(如120,343,275 等)，那么所有凸数的个数为________．

答案：1.36；2.13；3.6；4.240.

二、立体几何（上接第41页）

（2018年江苏理科卷第22题）如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．

（1）求异面直线BP与AC1所成角的余弦值；

（2）求直线CC1与平面AQC1所成角的正弦值．

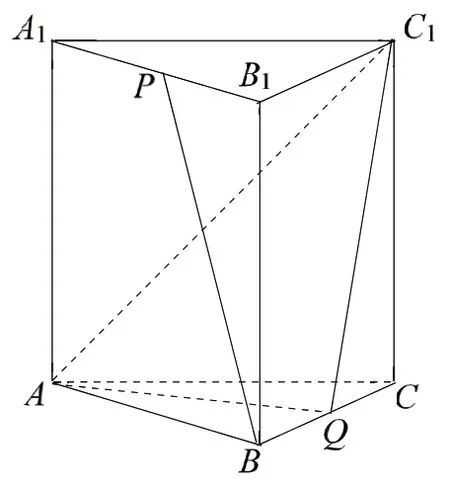
图1

三、圆锥曲线（上接第47页）

1.（2019年天津理科卷第5题）已知抛物线y2=4x的焦点为F，准线为l．若l与双曲线的两条渐近线分别交于点A和点B，且AB=4OF（O为原点），则双曲线的离心率为（ ）

2.（2019年浙江卷第15题）已知椭圆的左焦点为F，点P在椭圆上且在x轴的上方，若线段PF的中点在以原点O为圆心，OF为半径的圆上，则直线PF的斜率是________．

3.（2019年全国III 卷第15题）设F1，F2为椭圆C：的两个焦点，M为C上一点且在第一象限，若△MF1F2为等腰三角形，则M的坐标为___________．