例析运用放缩法证明数列求和不等式的策略
2020-07-14贵州省黔西第一中学
贵州省黔西第一中学
放缩法是一种有意识地对相关的数或者式子的取值进行放大或缩小的方法.证明数列求和不等式通常采用放缩法,这类题对学生的思维层次、综合应用能力的要求较高,如果把证明数列求和不等式与函数的导数相结合,将会出现在高考试卷的压轴题位置,这需要借助放缩技巧才能比较完美地解答,对考生而言,充满挑战.
放缩法中“放”的过程是指:要证明A<B成立,先将A放大成中间量C,即A<C,后证C<B;“缩”的过程是指:要证明A>B成立,先将A缩小成中间量C,即A>C,后证C>B.而以数列求和为背景的不等式证明过程常常借助特殊数列求和、分项求和、倒序相加求和、裂项相消求和、错位相减求和等方法.如何把握放缩的尺度,做到“恰如其分”,就需要把握放缩的策略,包括类型辨识策略和精确度控制策略.
一、类型辨识策略
观察要求证的不等式形式,分析式子可以放缩成什么求和类型.常见数列求和不等式的结构模型为(或者类型辨识即为观察数列{an}的形式,分析an可以放缩成什么类型的bn,从而使用数列求和方法达到化简的目标.
1 等比求和型
不等式中数列的通项与等比数列通项公式相似,如果不能直接使用等比数列求和公式,则将数列{an}的通项放缩成等比数列的通项,进一步求和化简.
例1(2014年高考全国Ⅱ卷文理第17(2)题) 已知数列{an}的通项公式证明:
分析由要证明的不等式从左到右需要“放大”,联想到“糖水不等式”:若a>b>0,则可将式子“放大”成即就可以使用等比数列求和公式.
解由
所以

命题得证.
后记此题容易落入将分母上的-1“丢掉”的陷阱,将分母上的-1“丢掉”也能化成等比数列的通项但是这个过程是“缩小”,即与所要证明的不等式形式不同.
同类型题(2016年高考四川卷理科第19(2)题):已知数列{en}的通项公式为证明:
2 裂项相消型
有的数列通项公式是分式,可以分裂成两项之差,求和后再放缩.但如果数列的通项公式不能分裂成两项之差时,可先把通项公式放缩后裂项,每一项按照相同的规律放缩后裂项,求和后再放缩.
例2(2013年高考广东卷文科第19(3)题)已知数列{an}的通项公式为an=2n-1,n ∈N∗,证明:对一切正整数n,都有
分析这个不等式从左到右需要“放大”,由可以采用裂项相消求和,再放缩.
解由所以

不等式得证.
事实上,例1也可以放缩成裂项相消型,参看文[1].
3 特殊不等式型
运用基本不等式、x+1≤ex、x-1≥lnx等特殊不等式进行放缩,尤其有些函数题第(1)问证明一个特殊不等式,第(2)问就运用这个不等式证明另一个不等式.
例3(2017年高考全国III卷第21题)已知函数
(1)若f(x)≥0,求a的值;
(2)设m为整数,且对于任意正整数求m的最小值.
分析观察式子是n项的乘积,而函数f(x)的解析式中含有对数,于是联想到将真数的乘积转化为对数的和,从而进行放缩再求和.
解第(1)问解答略,可得a=1;
(2)由(1)知,当x ∈(1,+∞)时,x-1-lnx>0,即lnx<x-1,所以因为

二、精确度控制策略
即使确定了需要放缩的不等式的类型,知道目标是什么,证明数列求和不等式也未必能“一帆风顺”,按照常规经验放缩有可能“放”得过大或者“缩”得过小,此时得考虑选择合适的式子或者留下部分项精确计算,从中间某一项开始放缩.
1 选择合适式子
例4(昆明市2020届昆一中联考卷四理科第21题改编)证明:
分析这个式子从左到右需要“放大”,也就是将分母减小,一个常规的想法是将分母(n+1)2减小为n(n+1),下面尝试这种放缩是否可行.
第一次尝试由所以

分析结果1比大,说明放得过大,原因是将(n+1)2减小为n(n+1)时,减少的值为n+1,这是随n增大而增大的数,能否将每项的分母减少固定的值,比如都减少1呢?
第二次尝试由
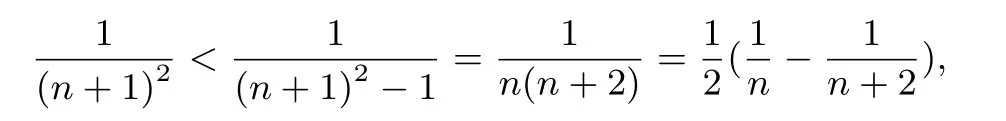
所以

分析结果虽然相对较小,但仍然比大.减1的目的是为了配成平方差,从而可以裂项相消,能否将每项的分母减少的值再小一点,比如呢?
第三次尝试由
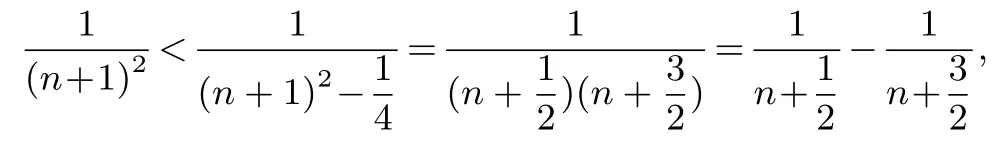

命题得证.
后记第三次尝试选择的式子是合适的,进一步思考能否将每项的分母减少的值再小一点?显然这是不行的,因为裂项之后要保证相邻两项能抵消,则裂开的两项的分母之差不能小于1,所以每项的分母减少时式子的值最精确.
2 留项计算
在已经辨识清楚不等式的类型,明确放缩的目标后,通过几次尝试仍然不能得到最精确的式子时,就需要留下不等式的前几项直接计算,从中间某一项开始放缩,提高放缩的精确度.
例5(2014年高考广东卷文科第19(3)题)已知数列{an}的通项公式为an=2n,n ∈N∗,证明:对一切正整数n,都有
分析确定这个式子可以放缩成裂项相消型,由根据常规思路“放大”到裂项相消以后得到的结果是“小于”,说明放得过大,但又不容易找到最精确的式子,于是采用留下前面的项直接计算.
解当n=1时,成立,当n>1时,由
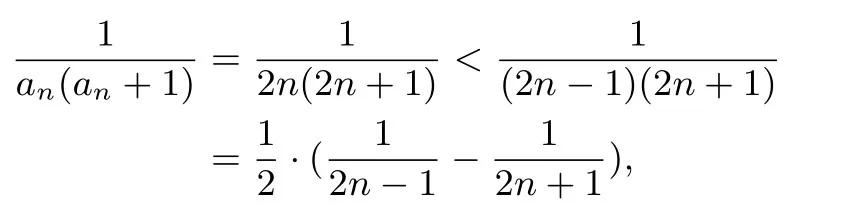
所以

命题得证.
同类题型(2013年高考广东卷理科第19(3)题)已知数列{an}的通项公式为an=n2,n ∈N∗,证明:对一切正整数n,都有
如果学生能够灵活运用放缩法,那么对其发现问题、提出问题、分析问题、解决问题的能力提升大有裨益,在解题中起到事半功倍的效果,同时也在提升学生逻辑思维能力、分析能力和创造能力中都很有帮助.在教学中教师应引导学生在放缩过程中学会观察、学会思考和学会表达,通过分析、归纳、总结,提升学生的数学逻辑推理、数学抽象、数学建模等核心素养.
