2020年美国数学竞赛(AMC12A)的试题与解答

2020-07-14华南师范大学数学科学学院

中学数学研究(广东) 2020年11期

关键词：骰子整数四边形

华南师范大学数学科学学院

1.Carlos took 70%of a whole pie.Maria took one third of the remainder.What portion of the original pie was left?

(A)10% (B)15% (C)20% (D)30% (E)35%

译文卡洛斯取走了一整块派的70%，玛利亚取走了剩余的三分之一.问这块派还剩下多少?

解(1-70%)×(1-)=20%，故(C)正确.

2.The acronymAMCis shown in the rectangular grid below with grid lines spaced 1 unit apart.In units，what is the sum of the lengths of the line segments that form the acronymAMC?

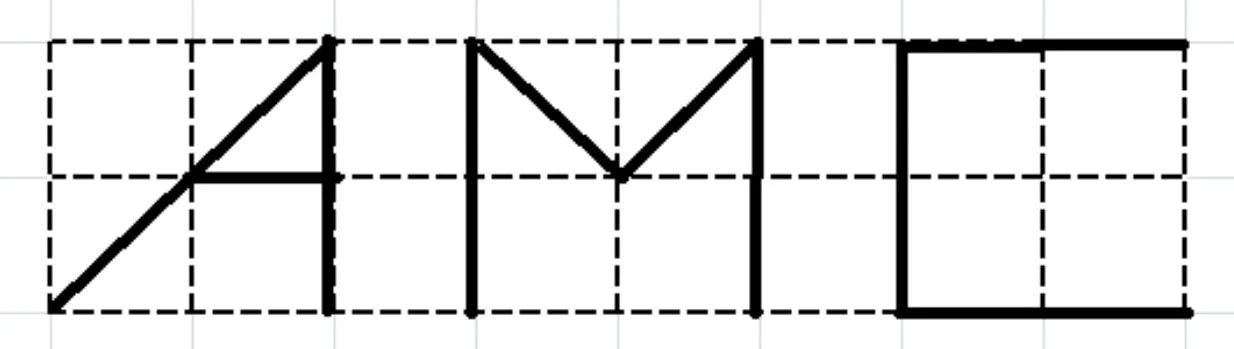
译文下图是矩形格子中的首字母缩写AMC，其中小正方形格子的边长为1.则字母AMC的线段长度之和是多少?

解观察图形可知，直线段长度和为13，而小正方形对角线长度为共4条，故总和为(C)正确.

3.A driver travels for 2 hours at 60 miles per hour，during which her car gets 30 miles per gallon of gasoline.She is paid$0.50 per mile，and her only expense is gasoline at$2.00 per gallon.What is her net rate of pay，in dollars per hour，after this expense?

(A)20 (B)22 (C)24 (D)25 (E)26

译文一位司机以60英里/小时的速度驾车2小时，她的车每跑30英里需要消耗1 加仑汽油.她能获得0.50美元/英里的报酬，唯一的花费就是2美元/加仑的汽油.问她每小时除去消耗之后的净收益是多少美元?

解1个小时她能跑60英里，获得60×0.50=30美元，汽油费为60÷30×2=4美元，故净收益为26美元，(E)正确.

4.How many 4-digit positive integers(that is，integers between 1000 and 9999，inclusive)having only even digits are divisible by 5?

(A)80 (B)100 (C)125 (D)200 (E)500

译文有多少个四位的正整数(也就是在1000和9999之间的整数)能被5整除且所有数字均为偶数?

解依题意，符合条件的四位数的个位数只能是0，十位数和百位数可以是0，2，4，6，8，千位数只能是2，4，6，8，共有1×5×5×4=100种选择，故(B)正确.

5.The 25 integers from-10 to 14，inclusive，can be arranged to form a 5-by-5 square in which the sum of the numbers in each row，the sum of the numbers in each column，the sum of the numbers along each of the main diagonals are all the same.What is the value of this common sum?

(A)2 (B)5 (C)10 (D)25 (E)50

译文将25个整数分别是从-10到14，放入5×5的格子中，使得格子里的每行、每列和两条对角线的数字和均相等.问这个数字和是多少?

解这是一个5阶幻方问题，25个数字之和是(-10)+(-9)+···+13+14=50，分别放入5行，故每行的数字和是10，(C)正确.

6.In the place figure shown below，3 of the unit squares have been shaded.What is the least number of additional unit squares that must be shaded so that the resulting figure has two lines of symmetry?

(A)4 (B)5 (C)6 (D)7 (E)8

译文如下图所示，3个单元格被涂成阴影部分.问至少还需要把多少个单元格涂成阴影才能使整个图有两条对称轴?

解由于这是一个4×5的矩形，两条对称轴只可能是长和宽两条边的中垂线，从而至少有7个单元格需要填涂，如右图所示.故(D)正确.

7.Seven cubes，whose volumes are 1，8，27，64，125，216，and 343 cubic units，are stacked vertically to form a tower in which the volumes of the cubes decrease from bottom to top.Except for the bottom cube，the bottom face of each cube lies completely on top of the cube below it.What is the total surface area of the tower(including the bottom)in square units?

(A)644 (B)658 (C)664 (D)720 (E)749

译文七个立方体，体积分别是1，8，27，64，125，216，343个立方单位，依次按照体积大小由底到顶垂直地堆积成一座塔.除了最底部的立方体，每个立方体的底面都完全被下面的立方体的顶面覆盖.问这座塔的表面积(包括底面)是多少个平方单位?

解这七个数都是立方数，则这七个立方体的棱长分别是1，2，3，4，5，6，7，从而塔的侧面积为4×(12+22+...+72)=560，而上、下底面积之和为2×72=98，共658，故(B)正确.

8.What is the median of the following list of 4040 numbers?

1,2,3,...,2020,12,22,32,...,20202

译文下列4040个数：1,2,3,...,2020,12,22,32,...,2020的中位数是多少?

解由于442=1936,452=2025，从而以上数列按递增排列的话，就成为：1,12,...,4,22,...,1936,442,...,1976,1977,...,2020,452,462,...,20202此时，1976成为第2020个数，所求中位数为故(C)正确.

9.How many solutions does the equation tan(2x)=have on the interval[0,2π]?

(A)1 (B)2 (C)3 (D)4 (E)5

译文方程在区间[0,2π]上有多少个解?

解y=tan 2x是一个周期为、值域为R的函数，在一个周期内严格单调递增，是一个周期为4π、值域为[-1,1]的函数，在区间[0,2π]上严格单调递减.如图示，在区间内，这是y=tan 2x完整的周期，两条曲线均有一个交点；在区间上，这是y=tan 2x的半周期，两条曲线刚好也有一个交点.故共有5个交点，(E)正确.

10.There is a unique integernsuch that log2(log16n)=log4(log4n).What is the sum of the digits ofn?

(A)4 (B)7 (C)8 (D)11 (E)13

译文存在唯一的整数n使得log2(log16n)=log4(log4n)成立，则n的各个数位上的数字之和是多少?

解log4(log4n)= log2(log16n)= log22(log16n)2，可得log4n=(log16n)2，使用换底公式有从而故(E)正确.

11.A frog sitting at the point(1，2)begins a sequence of jumps，where each jump is parallel to one of the coordinate axes and has length 1，and the direction of each jump(up，down，left，right)is chosen independently at random.The sequence ends when the frog reaches a side of the square with vertices(0，0)，(0，4)，(4，0)，and(4，4).What is the probability that the sequence of jumps ends on a vertical side of the square?

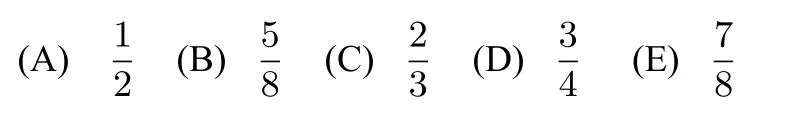
译文一只青蛙坐在点(1，2)上，开始一系列的跳跃，每次跳跃都平行于坐标轴且长度为1，方向(上、下、左、右)是随机的且独立，当青蛙到达由点(0，0)，(0，4)，(4，0)，(4，4)构成的正方形的一条边的时候，跳跃终止.问跳跃终止于正方形竖直的两条边上的概率是多少?

解如图示，青蛙在点F1处，它可以向四个方向跳跃，概率均为，向左跳跃，立刻达成目标；向上、向右、向下分别跳跃到点A1,C,A3处，再通过其它跳跃达成目标.根据对称性，青蛙由点A1,A2,A3,A4出发达成目标的概率是一样的，设为a；青蛙由点B1,B2出发达成目标的概率是一样的，设为b；青蛙由点F1,F2出发达成目标的概率是一样的，设为x；青蛙由点C出发达成目标的概率设为c.

因此，P(青蛙由F1出发达成目标)=P(青蛙向左)+P(青蛙向上)×P(青蛙由A1出发达成目标)+P(青蛙向右)×P(青蛙由C出发达成目标)+P(青蛙向下)×P(青蛙由A3出发达成目标)，即有

12.Linelin the coordinate plane has equation 3x-5y+40=0.This line is rotated 45°counterclockwise about the point(20，20)to obtain linek.What is thex-coordinate of thex-intercept of linek?

(A)10 (B)15 (C)20 (D)25 (E)30

译文坐标平面上的直线l的方程为3x-5y+40=0，其绕点(20，20)作逆时针旋转45°后得到直线k.则直线k与x轴交点的横坐标是多少?

解如图示，直线k与l的斜率分别为tan ∠1和tan ∠2，依题意有于是tan ∠1 =从而得到直线k的方程为y-20=4(x-20)，当y=0时，求得x=15.故(B)正确.

13.There are integera,bandc，each greater than 1，such thatfor allN＞1.What isb?

(A)2 (B)3 (C)4 (D)5 (E)6

译文设a,b,c均是大于1的整数，且式子对于N＞1均成立.问b是多少?

解

14.Regular octagonABCDEFGHhas arean.Letmbe the area of quadrilateralACEG.What is

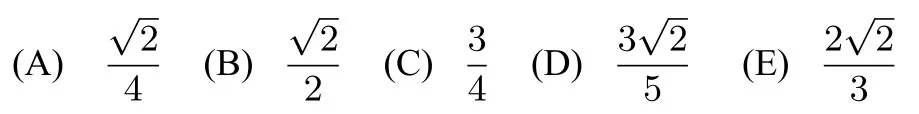
译文设正八边形ABCDEFGH的面积为n，四边形ACEG的面积为m.则是多少?

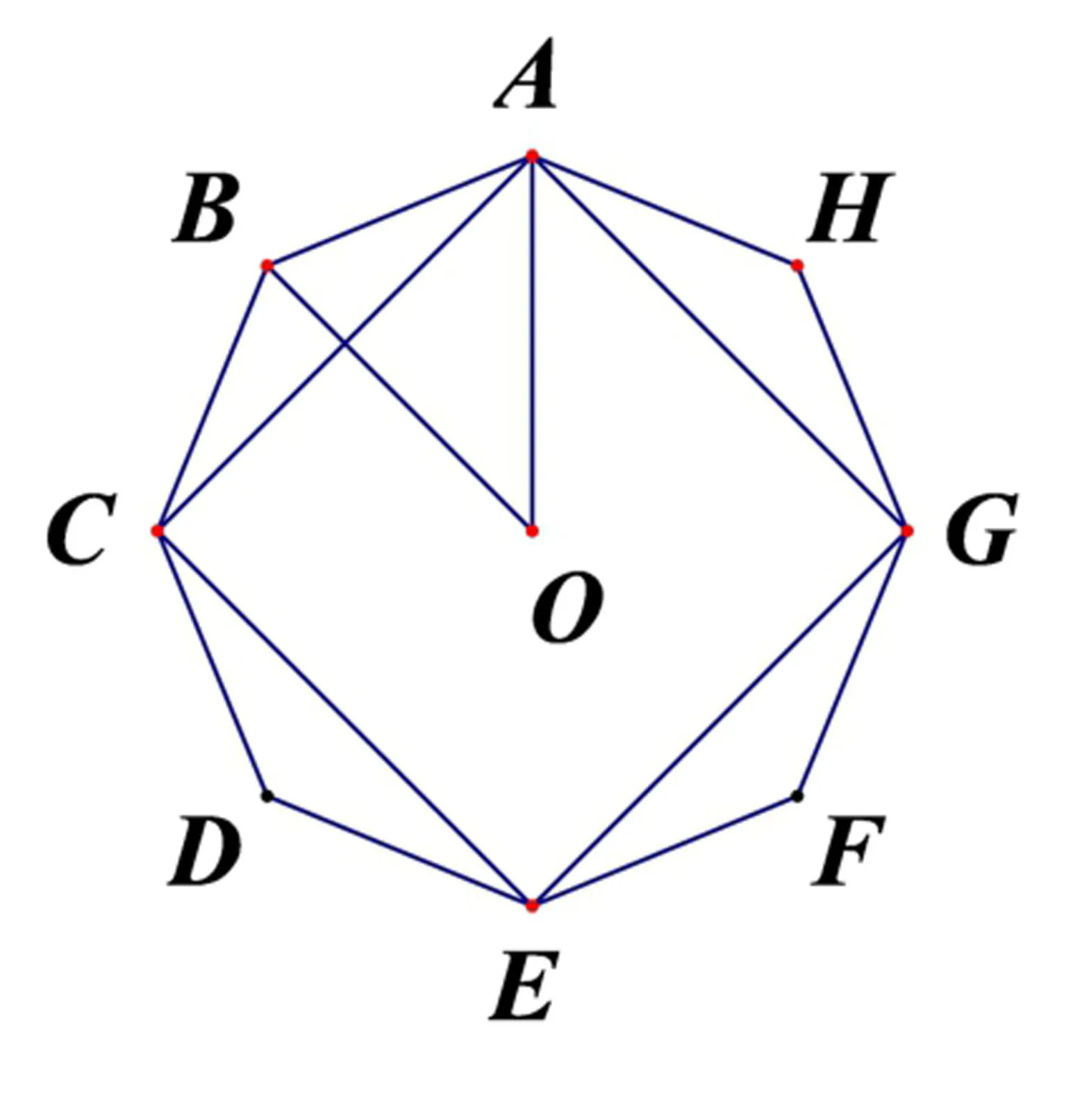
解如图，取正八边形的中心点O，连OA，OB.令OA=a，则AC=于是从而得故(B)正确.

15.In the complex plane，letAbe the set of solutions toz3-8=0 and letBbe the set of solutions toz3-8z2-8z+64=0.What is the greatest distance between a point ofAand a point ofB?

译文在复平面上，设A是方程z3-8=0的解集，B是方程z3-8z2-8z+64=0的解集.问A中一点到B中一点的最远距离是多少?

解解方程z3-8 =(z-2)(z2+2z+4)= 0，得解方程z3-8z2-8z+64=(z-8)(z2-8)=0，得容易看出A到B的最远距离为故(D)正确.

16.A point is chosen at random within the square in the coordinate plane whose vertices are(0，0)，(2020，0)，(2020，2020)，and(0，2020).The probability that the point lies withindunits of a lattice point is.(A point(x,y)is a lattice point ifxandyare both integers.)What isdto the nearest tenth?

(A)0.3 (B)0.4 (C)0.5 (D)0.6 (E)0.7

译文坐标平面上有一个以(0，0)，(2020，0)，(2020，2020)和(0，2020)为顶点的正方形.在正方形内随机选择一个点，该点位于格点的d个单位内的概率是(点(x,y)称为格点，若x和y均为整数.)则d精确到十分位是多少?

解如图示，以格点为圆心，d为半径作一些圆，则正方形内的圆内部分就是符合条件的点集.因此，该点落在此区域的概率为即求得故(B)正确.

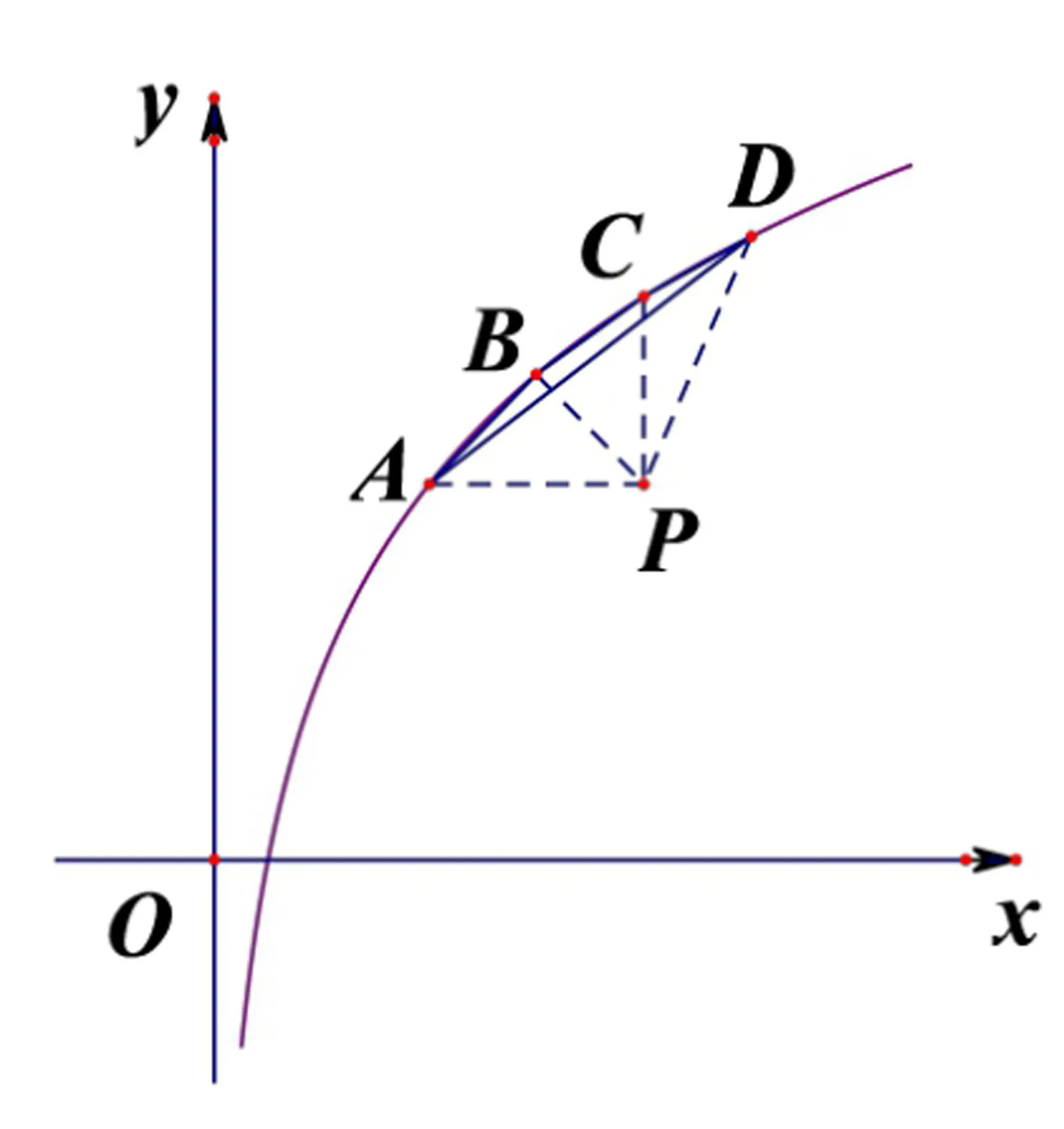
17.The vertices of a quadrilateral lie on the graph ofy=lnx，and thex-coordinates of these vertices are consecutive positive integers.The area of the quadrilateral is lnWhat is thex-coordinate of the leftmost vertex?

(A)6 (B)7 (C)10 (D)12 (E)13

译文一个四边形的顶点均在y=lnx的图像上，且它们的横坐标是连续正整数.该四边形的面积为ln则最左边顶点的横坐标是多少?

解如图示，ABCD是y=lnx上的四边形，过A作x轴的平行线，过C作x轴的垂线，交于点P，连结PB，PD，设点A坐标为(x,lnx)，则有B(x+1,ln(x+1))，C(x+2,ln(x+2))，D(x+3,ln(x+3))，P(x+2,lnx)，于是

18.QuadrilateralABCDsatisfies ∠ABC=∠ACD=90°，AC=20 andCD=30.Diagonalsandintersects at pointEandAE=5.What is the area of QuadrilateralABCD?

(A)330 (B)340 (C)350 (D)360 (E)370

译文四边形ABCD满足∠ABC=∠ACD=90°，AC=20，CD=30.对角线和交于点E，且AE=5.求四边形ABCD的面积是多少?

解如图示，以AC为直径作一个圆，交BD与点F，依题意可得设BE=x，依据相交弦定理AE·EC=BE·EF，则得再由切割线定理DC2=DF·DB，得解得或(舍去).而可得SΔABC=60，故SABCD=360，(D)正确.

19.There exists a unique strictly increasing sequence of nonnegative integersa1＜a2＜···＜aksuch that2a1+2a2+···+2ak.What isk?

(A)117 (B)136 (C)137 (D)273 (E)306

译文存在唯一严格递增的非负整数列a1＜a2＜···＜ak使得+2a2+···+2ak，则k是多少?

解令217=x，则-x15+x14-x13+···+x2-x+1,而x16-x15=2272-2255=2271+2270+···+2255，同理x14-x13=2238-2221=2237+2236+···+2221,···,x2-x=234-217=233+232+···+217.

从而

共8×17+1=137项，故(C)正确.

20.LetTbe the triangle in the coordinate plane with vertices(0，0)，(4，0)，and(0，3).Consider the following five isometries(rigid transformations)of the plane：rotation of 90°，180°，and 270°counterclockwise around the origin，reflection across thex-axis，and reflection across they-axis.How many of the 125 sequences of three of these transformations(not necessarily distinct)will returnTto its original position?(For example，a 180°rotation，followed by a reflection across thex-axis，followed by a reflection across they-axis will returnTto its original position，but a 90°rotation，followed by a reflection across thex-axis，followed by another reflection across thex-axis will not returnTto its original position.)

(A)12 (B)15 (C)17 (D)20 (E)25

译文设T是坐标平面上以(0，0)，(4，0)和(0，3)为顶点的三角形.考虑以下五种平面上的等距变换(刚体变换)：绕原点作90°，180°和270°的逆时针旋转，关于x轴或y轴的反射.任选三种变换(不必不同)可以组成125种组合，有多少种组合将使得T变回起始位置?(例如，一个关于y轴的反射，接着一个关于x轴的反射，再接着一个180°的旋转，将会使得T变回起始位置；但一个关于x轴的反射，接着另一个关于x轴的反射，再接着一个90°的旋转，将不会使得T变回起始位置.)

解分两种情况：(1)全部由旋转组成：只要三次旋转的角度和为360°或720°即可满足要求，因此有90°+90°+180°，90°+180°+90°，180°+90°+90°，270°+270°+180°，270°+180°+270°，180°+270°+270°共6种组合；

(2)由旋转和反射组合而成：有y轴+x轴+180°，y轴+180°+x轴，180°+x轴+y轴，180°+y轴+x轴，x轴+180°+y轴，x轴+y轴+180°，也是6种组合.故(A)正确.

21.How many positive integersnare there such thatnis a multiple of 5，and the least common multiple of 5! andnequals 5 times the greatest common divisor of 10! Andn?

(A)12 (B)24 (C)36 (D)48 (E)72

译文有多少个正整数n，使得n是一个5的倍数，且n与5!的最小公倍数是n与10!的最大公因数的5倍?

解由题意，[n,5!]=5×(n,10!)，而5!=23×3×5,10!=28×34×52×7，可知n不含除2，3，5，7以外的素因子，可设n=2a×3b×5c×7d，其中a,b,c,d ∈N，且c≥1.

根据[2a×3b×5c×7d,23×3×5]= 5×(2a×3b×5c×7d,28×34×52×7)，以及最大公因数和最小公倍数的取法，可得3≤a≤8,1≤b≤4,c=3,0≤d≤1.故n有6×4×1×2=48种取法，(D)正确.

22.Let(an)and(bn)be the sequence of real numbers such What is

译文设(an)和(bn)是使(2+i)n=an+bni 对所有的整数n≥0均成立的实数列，其中则是多少?

解由(2+i)n=an+bni，可得(2-i)n=an-bni，两式相加减得

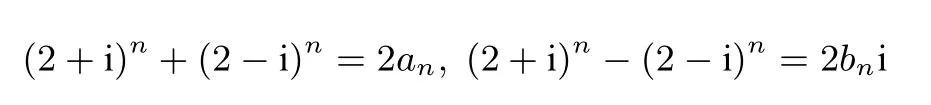
从而

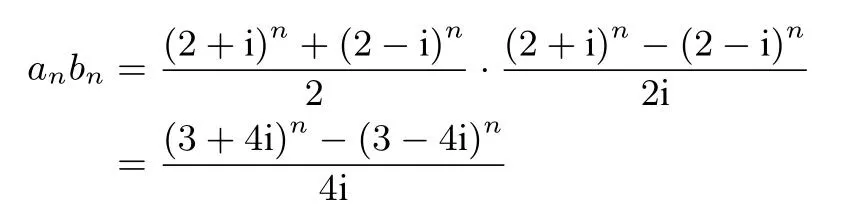
于是

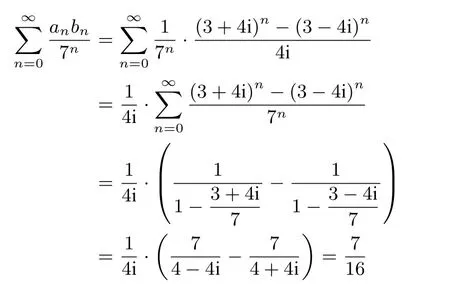
故(B)正确.

23.Jason rolls three fair standard six-sided dice.Then he looks at the rolls and chooses a subset of the dice(possibly empty，possibly all three dice)to reroll.After rerolling，he wins if and only if the sum of the numbers faces up on the three dice is exactly 7.Jason always plays to optimize his chances of winning.What is the probability that he chooses to reroll exactly two of the dice?

译文詹森掷3颗标准、均匀的骰子，他看了结果之后会选择若干(可能是0，也可能是3)颗重掷.当3颗骰子正面朝上的数字和为7点的时候，他就赢了.詹森总是按照朝着他赢的最优策略去掷.问他刚好选择2颗骰子重掷的概率是多少?

解掷1颗骰子得1，2，3，4，5，6点的概率均为掷2颗骰子得3点只有两种情况：12和21，概率为，···；掷3颗骰子得7点有15种情况：115，151，511，124，142，214，241，412，421，133，313，331，223，232，322，概率为经过计算，所有结果如下表所示：

分类/概率/结果1 2 3 4 5 6 7掷1颗1 6 1 6 1 6 1 6 1 6 1 6掷2颗1 36 2 36 3 36 4 36 5 36掷3颗1 216 3 216 3 216 10 216 15 216

因此，詹森要选择2颗骰子重掷，则上次掷的结果中，任意两颗骰子的数字和不能小于7点，否则他将选择重掷1颗骰子；且不能3颗骰子都是4点或者以上，要不然他将选择that(2+i)n=an+bni for all integersn≥0，where i=重掷3颗骰子.根据以上分析，满足条件的情况有：(1)掷出1点、6点、6点，3种情况；(2)掷出2点、5点、5点，3种情况；(3)掷出2点、5点、6点，6种情况；(4)掷出2点、6点、6点，3种情况；(5)掷出3点、4点、4点，3种情况；(6)掷出3点、4点、5点，6种情况；(7)掷出3点、4点、6点，6种情况；(8)掷出3点、5点、5点，3种情况；(9)掷出3点、5点、6点，6种情况；(10)掷出3点、6点、6点，3种情况.

24.Suppose that ΔABCis an equilateral triangle of side lengths，with the property that there is a unique pointPinside the triangle such thatWhat iss?

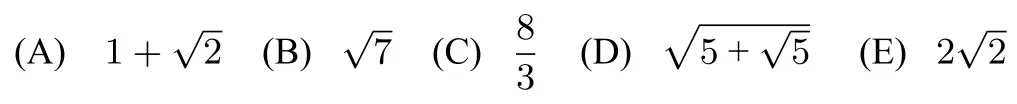
译文设ΔABC是一个边长为s的正三角形，内部有一点P，使得问s是多少?

解如图，将ΔAPC绕点A逆时针旋转60°，得到ΔADB，连结DP，则AD=AP=1，DB=PC=2，∠DAP=60°，因而ΔADP是一个正三角形，可得DP=1，进而DP2+BP2=DB2，所以ΔDPB是一个直角三角形，∠DPB=90°，因此∠APB=150°.根据余弦定理，s2=AB2=AP2+PB2-即得故(B)正确.