用裂项相消法解多类数列求和问题

安徽省芜湖市第一中学

数列是高中数学的重要内容之一，数列求和更是高考常考问题，数列求和主要有公式法、裂项相消法、错位相减法、并项转化法、分组转化法等.笔者发现，很多时候我们可以通过待定系数法构造数列{bn}满足an=bn+1-bn，利用裂项相消法来对数列{an}求和，一步到位得到Sn=bn+1-b1，这样的做法可以大大的减少计算量，提高解题效率，现通过具体例题介绍这种做法，供读者参考学习.

1 解决公式法求和问题

例1求12+22+32+···+n2.

解析令an=n2，问题转化为求数列{an}的前n项和.构造数列{bn}满足an=bn+1-bn，设bn=xn3+yn2+zn，则x(n+1)3+y(n+1)2+z(n+1)-(xn3+yn2+zn)=n2，整理得3xn2+(3x+2y)n+x+y+z=n2，所以3x=1，3x+2y=0，x+y+z=0，解得故

点评自然数平方和公式常见的证明方法有两种，一是先通过不完全归纳法猜想再用数学归纳法证明，这种方法虽容易，但计算繁琐；二是利用公式n3-(n-1)3=3n2-3n+1迭加，这种方法的技巧性很强，一时难以想到.在这里，将n2构造成数列{bn}的前后两项之差，最后成为裂项相消求和形式，一步到位得到答案.

2 解决错位相减法求和问题

例2求公比为q(q1)的等比数列{an}的前n项和.

解析由题知an=a1qn-1，构造数列{bn}满足an=bn+1-bn，设bn=xqn，则xqn+1-xqn=a1qn-1，解得所以故

点评等比数列求和公式课本上是用错位相减法推导得到的，利用待定系数法构造新数列裂项相消求和大大简化了计算.另外我们也可以通过

直接裂项求和，但是此法技巧性强，难以想到.

例3已知数列{an}为等差数列，前n项和Sn(n ∈N∗)，{bn}是首项为2的等比数列，且公比大于0，b2+b3=12，

(1)求{an}和{bn}的通项公式；

(2)求数列{a2nb2n-1}的前n项和Tn.

解析(1)设等差数列{an}的公差为d，等比数列{bn}的公比为q(q＞0).由题知解得q=2，则bn=2n，所以a4-2a1=8，S11=11×16，即3d-a1=8，11a1+55d=11×16，解得d=3，a1=1，则an=3n-2.

(2)由(1)得a2nb2n-1=(6n-2)22n-1=(3n-1)4n，构造数列{cn}满足a2nb2n-1=cn+1-cn，设cn=(xn+y)4n，则(x(n+1)+y)4n+1-(xn+y)4n=(3n-1)4n，整理得3xn+4x+3y=3n-1，则3x=3，4x+3y=-1，解得所以故

点评对于等差乘等比型数列，通常的做法是错位相减法.虽然错位相减法是一种固定模式的做法，学生容易掌握，但是计算繁琐复杂，学生在实际解题时会做却难以算出正确结果，而用待定系数法构造数列{bn}使得an=bn+1-bn，很容易裂项相消求出结果.

3 解决并项转化法求和问题

例4已知数列{an}的前n项和Sn=2n2-n.

(1)求数列{an}的通项公式；

(2)若bn=(-1)nan，求数列{bn}的前n项和Sn.

解析(1)n≥2时，

又a1=1，所以an=4n-3.

(2)由(1)得bn=(-1)n(4n-3)，构造数列{cn}满足bn=cn+1-cn，设cn=(-1)n(xn+y)，则

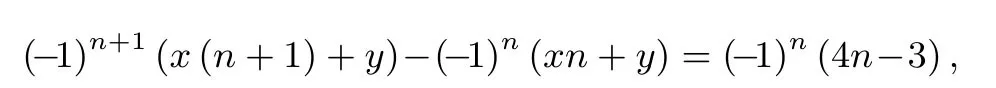
整理得2xn+x+2y=-4n+3，解得则故

点评对于通项公式是an=(-1)nf(n)的数列求和，还可以采用并项转化求和，如本题可以构造数列{dn}满足dn=b2n-1+b2n=4，然后对项数n分奇偶数讨论，得

4 解决分组转化法求和问题

例5在数列{an}中，a1=1，a2=3，an+2=3an+1-2an.

(1)证明数列{an+1-an}是等比数列，并求数列{an}的通项公式；

(2)若bn=4log2(an+1)+3，求数列{(-1)nbnbn+1+n·2n}的前n项和Tn.

解析(1)由题得an+2-an+1=2(an+1-an)，且a2-a1=2，则数列{an+1-an}是首项为2，公比为2的等比数列，所以an+1-an=2n.n≥2时，

又a1=1，因此an=2n-1.

(2)由(1)得bn=4n+3，则

构造数列{cn}满足(-1)nbnbn+1+n·2n=cn+1-cn，设cn=(-1)n(xn2+yn+z)+(sn+t)2n，则

整理得

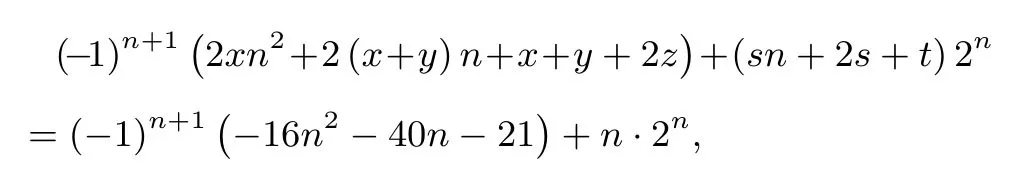
所以2x=-16，2(x+y)=-40，x+y+2z=-21，s=1，2s+t=0，解得x=-8，y=-12，

则

故

点评本题也可以用分组转化求和，数列{(-1)nbnbn+1+n·2n}的通项可以分为两个部分，一是数列{(-1)nbnbn+1}，用并项转化求和得二是数列{n·2n}，用错位相减求和得(n-1)2n+1+2.

5 解决特殊数列{(An2+Bn+C)qn}求和问题

例6已知数列{an}满足a1=2，an+1-an=2(n+1).

(1)求数列{an}的通项公式；

解析(1)n≥2时，

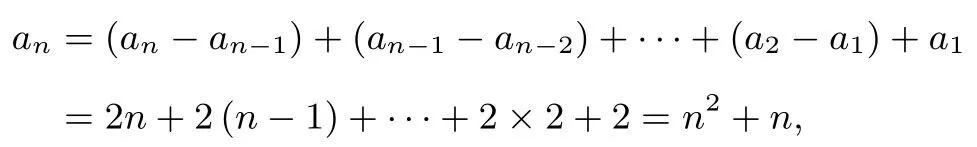
又a1=2，因此an=n2+n.

(2)由(1)得anbn=(n2+n)构造数列{cn}满足anbn=cn+1-cn，设cn=(xn2+yn+z)则

整理得-xn2+(2x-y)n+x+y-z=2n2+2n，所以-x=2，2x-y=2，x+y-z=0，解得x=-2，y=-6，z=-8，故

因此Sn=cn+1-c1=

点评对于数列平常所用的数列求和法是求不出它的前n项和的，但是通过待定系数法构造数列{cn}，使得接着利用裂项相消法求和即可得到答案.

本文介绍的通过待定系数法构造新数列，再利用裂项相消法求和，为我们提供了一种新的数列求和方法，但是同学们在日常学习中，要结合自身掌握程度和实际情况，选择最佳的求和方法，不要一味追求某一种解法，要学会从不同解法中汲取不同的数学思想，提高自身的数学核心素养.