“以直代曲”思想在函数中的应用

深圳实验学校高中部

在近几年的全国高考压轴题、数学竞赛题中，常常遇到与指数类函数、对数类函数、二次函数等非直线型的函数不等式，这类不等式多数是与函数零点、数列求和有关，用“以直代曲”思想方法对这类不等式进行证明，往往更方便、更简单.下面谈谈“以直代曲”思想方法在函数中的一些应用.

一、利用切线或割线来逼近曲线

在数学上最容易处理的函数是线性函数，通过将函数在局部转化为线性函数，是我们处理问题时达到简单、方便、高效的目的.

我们知道如果连续函数f(x)(x ∈(a,b))在(a,b)上是上凸函数(f′′(x)＜0)，y=g(x)是曲线y=f(x)在(a,b)上的一条切线，y=h(x)是连结点A(a,f(a))、B(b,f(b))的一条割线，则当x ∈(a,b)时，h(x)＜f(x)≤g(x)(如图1)；反之，若f(x)是下凸函数(f′′(x)＞0)，则当x ∈(a,b)时，h(x)＞f(x)≥g(x)(如图2).

例如函数f(x)= lnx是上凸函数，曲线y=f(x)在点(1,0)处的切线为y=x-1，则有lnx≤x-1，同理有不等式ex≥x+1，这两个不等式就是我们经常使用的不等式.

1 利用“以直代曲”证明不等式

利用切线或割线来逼近曲线进行放缩，是证明不等式的一种重要方法.

例1已知f(x)=xlnx-a,a＜0，设x1,x2(x1＜x2)是函数f(x)的零点，求证：ea+1＜x2-x1＜2a+1+e-2(e是自然对数的底数).

分析由于函数y=xlnx是下凸函数，曲线的切线都在图像下方，则可构造两割线、两切线分别证明左、右两边不等式.

证明函数f(x)的零点即方程xlnx=a的解，令g(x)=xlnx，因为则函数g(x)为下凸函数，函数y=g(x)的图像与直线y=a交于两点(x1,a)、(x2,a)(如图3).

图3

图4

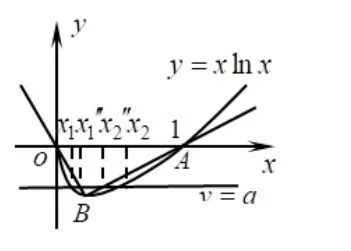
图5

设曲线y=g(x)在x=e-2和x=1处的切线分别为l1:y=-x-e-2和l2:y=x-1，直线y=a与直线l1、l2分别交于点(x′1,a)、点(x′2,a)(如图4)，则有x′1＜x1＜x2＜x′2.因为x′1=-a-e-2，x′2=1+a，所以x2-x1＜x′2-x′1=(a+1)-(-a-e-2)=2a+1+e-2.

由g′(x)= 0，得设经过原点O和点的割线为l1′:y=-x，经过点A(1,0)和点的割线为直线y=a与直线l1′、l2′分别交于点(x1′′,a),(x2′′,a)(如图5)，则有x1＜x1′′＜x2′′＜x2.又因为x1′′=-a，x2′′=(e-1)a+1，所以因此，原不等式成立.

2 利用“以直代曲”求最值

例2已知函数设且a+b+c=3，若不等式f(a)+f(b)+f(c)≤λ恒成立，求实数λ的最小值.

分析由于条件中给出a+b+c=3，则需将f(x)放缩成关于kx+m的形式，又由于a,b,c在条件中处在等价对称位置，因此，可考虑用曲线y=f(x)在x=1处的切线来逼近曲线y=f(x).

解函数f(x)在x=1处的切线为y=4-x，因为当时，所以f(x)≤4-x.所以f(a)+f(b)+f(c)≤(4-a)+(4-b)+(4-c)=12-(a+b+c).

因为a+b+c=3，所以f(a)+f(b)+f(c)≤12-3=9.故要使不等式f(a)+f(b)+f(c)≤λ恒成立，必须λ≥9.又因为 当a=b=c=1时，满足条件a+b+c=3，且f(a)+f(b)+f(c)=9，因此，λ的最小值为9.

例3已知求的最大值.

分析给出的条件和需求的代数式都不是关于a,b,c的对称式，若进行换元，令6a=2x2,3b=2y2,2c=2z2，则命题转化为在满足条件x+y+z=3 下，求的最大值.此时条件和需求的代数式都是关于x,y,z的对称式，则可考虑用曲线在x=1处的切线进行放缩求最值.

解设6a=2x2,3b=2y2,2c=2z2，则x+y+z=3，

下面证明当0≤x≤3时，不等式成立.因为

又因为当x ∈[0,3]时，有2x3-3x2-8x-13 =x2(x-3)+x(x2-9)+x-13＜0，所以不等式成立，即则有

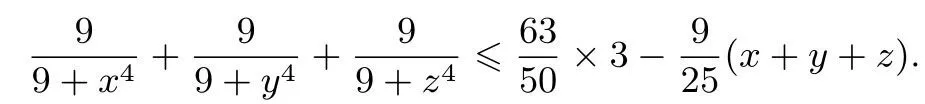
因为x+y+z=3，所以等号当x=y=z=1时取得，因此，所求最大值为

二、利用矩形来逼近曲边梯形

根据定积分定义我们知道，如果函数f(x)在[a,b]上连续，则其中

将区间[a,b]等分成n个小区间，如果f(x)在[a,b]上单调递减，且f(x)＞0，根据函数图像，则f(x)在第i个小区间上的曲边梯形面积大于且小于因此，根据定积分定义可以得到下列不等关系：

图6

图7

如果f(x)在[a,b]上单调递增，则得到与上述不等式相反的结论.因此，对一些求和型的不等式(或我们可以通过构造函数，根据函数的单调性，利用定积分定义进行证明.

例4(2009年全国高中数学联赛加试)求证不等式：

分析因为所以可看成是n个小矩形面积的和.若将每个小矩形放缩成曲边梯形，则可利用定积分定义证明该不等式.

证明令则f(x)在(1,+∞)单调递减，所以因为

总之，“以直代曲”思想本质上是利用非线性函数在定义域内某个区间上的凸性，恰当利用切线、割线或矩形，将函数值运算放缩为线性运算或较简单的代数式运算.对于一些不等式的证明问题和最值的求解问题，运用“以直代曲”方法，往往能化繁为简.