多参非解析4旋转对称映射的动力系统图形化研究

陈 宁，张书玮，王凤英

(沈阳建筑大学 信息与控制工程学院，沈阳 110168)

1 引 言

随着计算机的软硬件设备的逐步开发与完善,非线性动力系统图形化的研究成为了非线性科学的一个研究分支.美国科学家B.B.Mandelbrot于上世纪70年代采用复解析映射f(z)=z2+c在参数平面上构造出了著名的Mandelbrot集合(M集),这个集合被称之为是一个构造动力平面上结构各异的充满Julia集分形图的源泉[1].研究人员针对不同的迭代映射提出动力系统图形化的各种方法,大量生成了各种形式的充满Julia集分形图和混沌吸引子图[2-8].在非线性动力系统的图形化研究中,用线性仿射压缩迭代函数系(IFS)构造分形是另一个重要的研究内容,2000年以来,在构造IFS的新方法研究、IFS自身的各种数学性质、利用IFS构造重叠分形、超分形的方法研究以及广义IFS与编码空间之间关系的相关成果不断出现[9-13]；来自于IFS的分形在各工程领域的应用研究也取得了进展[14-16]；随着IFS的越来越广泛的应用,对线性迭代函数系所生成的分形的研究进入到了对非线性迭代函数系的相关研究[17-20].1991年,Vrscay和Weil用实多项式进行了的非线性IFS构造奇怪吸引子的研究[17].2009年,王兴元等人将Vrscay和Weil的模型扩展成复多项式映射[18],他们模拟了用上述复映射构造的IFS的分形吸引子,讨论了完全离散的IFS的吸引子与它的地址集之间的关系,理论分析了控制参数变化对图形结构变化规律的影响.同年,Van Loocke用2个线性的压缩映射和2个包括复变量平方根的映射构造了由4个映射组成的非线性IFS,在正多边形和圆上生成了分形图案[19].2010年,清华大学范申的博士论文《非线性迭代函数系与Schrödinger算子的谱的分形性质》[20],关于一列有向图确定的非线性迭代函数系的有界变差、有界谐变与Gibbs-Lik测度存在性等问题进行了深入的理论研究.

2 搜索迭代映射的极值点

(1)

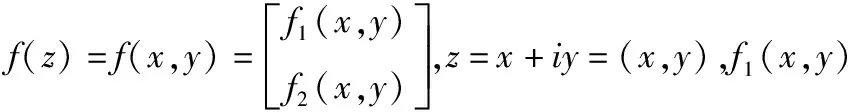
(2)

min‖Df(x,y)‖

(3)

(4)

是一个在动力平面上具有4个90°旋转对称的迭代映射,可以在第一象限搜索指定参数下迭代映射的局部极值点.实验表明：这个映射的混沌吸引子以及充满Julia集的吸引域范围可以控制在(x,y∈[-1.5,1.5])之内,因此,关于式(4),本文取动力平面的第一象限且(x,y∈[0,1.5])为指定参数下的迭代映射局部极值点的基本搜索域,以0.1为步长,在基本搜索域上共取16×16=256个初始点,用“步长加速法”搜索出在迭代终止限10-6下的满足式(3)的N个局部极值点(其中N值随参数变化而变化),为在参数空间划分出不同动力学特性的参数区间,即构造广义M集做出了必要准备.

表1给出了在式(4)的参数空间上选取7个参数的7个迭代映射在基本搜索区域上遍历256个初始点,用“步长加速法”搜索出的互不相同的局部极值点.表中各迭代映射中的参数(α,β,γ)取定值,参数(λ,ω)取变值,即将参数λ和ω组成了5参数空间的1个参数断面C,λ为水平坐标轴,ω为纵坐标轴,(ci,i=1,2,…,7)是参数断面C上的7个参数.表1说明:迭代映射(4)随着参数的变化,从基本域出发,搜索出的局部极值点的数量N是变化的,N个极值点的迭代轨道特性可以不同:有逃逸轨道、混沌轨道和吸引周期轨道;但N个极值点的轨道中可以具有相同的轨道特性,根据一个迭代映射在动力平面上的局部极值点的轨道特性将参数空间进行有效划分,构造出参数截断面上的广义M集.

表1 7 个参数下的迭代映射的动力学特性(其中α=-0.57087,β=1.30842,γ=-0.86886)

Table 1 Dynamics of iterative mapping under 7 parameters(whereα=-0.57087,β=1.30842,γ=-0.86886)

参数ci(λi,ωi)极值点数N极值点序号极值点坐标x yL指数极值点轨道特性轨道点的坐标或混沌吸引子c1(0.943,0.800)610.3809620.550630-0.776367I:8周期I:{(-0.002,-0.642),(0.510,-0.369),20.2010000.694208-0.776367(0.642,-0.002),(0.369,0.510),30.3119190.800219-0.776367(0.002,0.642),(-0.510,0.369),40.645168-0.199000-0.776367(-0.642,0.002),(-0.369,-0.510)}50.3994380.608469-0.77636760.800219-0.305460-0.776367c2(-0.669,0.482)71-0.0330770.601000-0.278318I:1周期I:{(0,0)}20.2010000.694713-0.278318I:1周期II:{(-0.905,0.164),(0.905,-0.164)}30.6176140.051000-0.278318I:1周期III:{(-0.164,-0.905),(0.164,0.905)}40.900219-0.103897-0.603969II:2周期50.1245670.900219-0.603969III:2周期6-0.0986090.744235—逃逸70.7553210.097875—逃逸c3(1.349,0.211)210.5011100.520618-0.135510I:2周期I:{(0.415,0.701),(0.596,0.566)}20.3244380.633841-0.135510c4(-0.669,0.388)710.1411180.301000-0.370764I:1周期I:{(0,0)}20.557250-0.031884-0.370764I:1周期II:{(-0.860,0.215),(0.940,-0.071)}30.894750-0.065432-0.345125II:2周期III:{(-0.215,-0.860),(0.071,0.940)}40.1254190.894750-0.345125III:2周期50.2010000.706669-0.345125III:2周期6-0.1052500.794159—逃逸70.8035110.101000—逃逸c5(0.719,1.022)210.2136900.6010000.247352I:混沌I:2个极值点的轨道到达同一个混沌吸引子20.615980-0.1990000.247352c6(-0.691,0.352)710.1349630.601000-0.366819I:1周期I:{(0,0)}20.563500-0.001074-0.366819I:1周期II:混沌吸引子130.894750-0.0516060.047041II:混沌III:混沌吸引子240.1212770.8947500.047041III:混沌50.2100000.7266830.047041III:混沌6-1.052520.808234—逃逸70.8157820.101000—逃逸c7(1.225,1.118)310.4010000.777790—逃逸—20.3051810.801000—逃逸30.793809-0.299000—逃逸

*表1中符号“—”意为轨道逃逸,不存在L指数也没有相应图形；表1中最后1项表示参数ci下的迭代映射fci(z)在动力平面上的吸引周期轨道上各周期点的坐标值或出现的混沌吸引子情况,用符号“I、II 和III”表示该参数映射下的不同情况.

3 参数空间截面C上的广义M集

式(4)的参数空间是5维的,由于计算屏幕可以清晰地表达由2个参数构成的参数截面上的参数区域划分情况,本文提出了通过在5个参数中固定3个参数,考查另2个参数变化对迭代映射的动力学特性的影响来构造参数断面上广义M集的方法.例如:本文采用固定3个参数(α,β,γ),将其余2个参数(λ,ω)组成一个参数空间截面C,构造出该断面上的广义M集.

在参数断面C上取不同参数点{ci,i=1,2,…,7}(见表1),相应迭代映射(4)在动力平面(XOY)上有不同的动力学特性,例如,表中参数c7下的迭代映射的3个局部极值点的轨道都逃逸了.图1显示了用“步长加速法”数值计算出的表1中前6个参数下的迭代映射的各局部极值点的迭代轨道,其中参数c1的6个极值点的轨道分别到达了同一条8吸引周期轨道；参数c2和参数c4下的7个极值点的轨道分别到达了各自迭代映射的吸引不动点I、2个2吸引周期轨道II和III以及逃逸轨道；参数c3下的2个极值点的轨道分别到达了同一条2吸引周期轨道I；参数c5下的2个极值点的轨道分别到达了同一个混沌吸引子I；参数c6下的7个极值点的轨道分别到达了一个吸引不动点I,2个混沌吸引子II和III以及逃逸轨道.参数不同,I、II和III代表的对象不同.图1打出了第1象限中16×16=256个搜索初始点的位置,绘图窗口为:{x∈[-1.5,1.5],y∈[-1.5,1.5]}.

图1 表1中各迭代映射的局部极值点轨道

本文在参数断面C上选绘图窗口{λ∈[-1.1,1.7],ω∈[-2,2]}为构造广义M集的参数区域范围.在768×768的分辨率下,遍历选取绘图范围内768×768组参数中的每一组(λ,ω)参数与固定的参数{α=-0.57087,β=1.30842,γ=-0.86886}一起构造出一个相应的迭代映射,用“步长加速法”搜索第1节所述的指定参数下的迭代映射的N个局部极值点.如果搜索出的N个局部极值点的所有迭代轨道均逃逸,则这个迭代映射在动力平面上的所有点的迭代轨道均逃逸,与参数断面C上的参数组(λ,ω)相应的绘图窗口内的像素点被着上白色,代表参数断面C上“逃逸区域”中的1点；如果搜索出的N个局部极值点的迭代轨道有逃逸的、且有吸引周期的(Li<0,1≤i≤N),则迭代映射在动力平面上有吸引周期轨道的吸引域,所有周期轨道的吸引域的并集是这个迭代映射的充满Julia集,与参数断面C上的参数(λ,ω)相应的绘图窗口内的像素点被着上黑色,代表参数断面C上“吸引参数”区域中的1点；如果搜索出的N个局部极值点的迭代轨道有逃逸的、且有混沌的(Li>0,1≤i≤N),则迭代映射在动力平面上有混沌吸引子,所有混沌吸引子的并集是这个迭代映射的总的混沌吸引子,与参数截面C上的参数(λ,ω)相应的绘图窗口内的像素点被着上深灰色,代表参数断面C上“混沌参数”区域中的1点；如果搜索出的N个局部极值点的迭代轨道有逃逸的、也可以没有逃逸的,但是既有混沌的也有周期的(Li>0或Lj<0|其中:1≤i，j≤N, 且i+j≤N),则迭代映射在动力平面上既有混沌吸引子也有充满Julia集,与参数断面C上的参数组(λ,ω)相应的绘图窗口内的像素点被着上浅灰色,代表参数断面C上“混合参数”区域中的1点.按照上述对参数区域的划分方法,本文构造出了参数截面C上的广义M集,表1中7个参数点{(λi,ωi),i=1,2,…,7}在M集中的位置如图2所示.本文称白色为逃逸参数区域,黑色为吸引参数区域,浅灰色为混合参数区域以及深灰色为混沌参数区域.黑色区域参数可以用于构造生成充满Julia集图形的迭代映射；浅灰色区域参数可以用于构造生成充满Julia集图形和混沌吸引子图形的迭代映射；深灰色区域参数可以用于构造生成混沌吸引子图形的迭代映射.

图2 复映射式(4)参数截面C上的广义M集

图3是采用图2(或表1)中前6组参数构造出的迭代映射在动力平面上的充满Julia集或混沌吸引子,图3中标出了各迭代映射在动力平面上的极值点的I、II和III轨道.观察与图3中参数c1,c2和c5相应的图形:图3(a)和图3(b)中的充满Julia集、图3(e)中的混沌吸引子都是4旋转对称的图形；而与参数c3,c4和c6的相应图形:图3(c)和图3(d)中的充满Julia集图形是不完整的4旋转对称图形；图3(f)中吸引不动点轨道I的吸引域所表示的充满Julia集是4旋转对称的图形,而与混沌轨道II和III相应的吸引子部分的图形不是4旋转对称的图形,因此,图3(f)的整体图形不是完整的4旋转对称图形.

图3 图2的M集上6个参数下的迭代映射的充满Julia集与混沌吸引子图

由于式(4)是具有Z4对称特性的迭代映射,因此,在第1象限搜索区域得到的局部极值点在动力平面上是Z4旋转对称分布的.如果搜索出所有这些旋转对称分布的极值点的轨道,就可以生成动力平面上的完整的Z4对称的充满Julia集或混沌吸引子图形.如图4所示,其中图4(a)表明参数c3下的迭代映射在动力平面上有4条旋转对称分布的2周期吸引轨道,因此相应的充满Julia集是这4条吸引周期轨道的吸引域的并集；图4(b)表明参数c4下的迭代映射在动力平面上有2组互成90°旋转对称分布的2周期吸引轨道和一条位于原点的1周期吸引轨道,共5条吸引周期轨道,因此相应的充满Julia集是这5条吸引周期轨道的吸引域的并集；而图4(c)表明参数c6下的迭代映射在动力平面上有4条旋转对称分布的混沌轨道,每条混沌轨道的混沌吸引子由两块混沌区域组成,参数c6下的迭代映射在动力平面上共有8块混沌区域组成；由于这个迭代映射在动力平面上还有一个在原点处的一周期吸引轨道,其吸引域就是这个迭代映射在动力平面上的充满Julia集,参数c6下的迭代映射在动力平面上既有充满Julia集又有混沌吸引子的完整的混合图形如图4(d)所示.

图4 图3中不完整图形的补充图形

图4表明,虽然根据在动力平面的1/4搜索区域上搜索出的局部极值点的轨道特性能将参数平面进行准确的区域划分,但从这样的参数区域挑选参数构造迭代映射并在动力平面上构造完整充满Julia集或混沌吸引子图形时,应该将搜索区域中获得的局部极值点进一步再旋转90°、180°和270°,以找到动力平面上的所有局部极值点,并考察所有局部极值点的轨道特性.关于λ参数轴对称分布的图5是本文对式(4)在图2的绘图区域上关于每组参数下的迭代映射在动力平面的基本搜索区域上用“步长加速法”搜索出的局部极值点,并根据其4旋转对称的所有局部极值点轨道的动力学特性来对参数点进行区域划分的广义M集.这个广义M集中白色仍表示逃逸参数区域、深灰色和浅灰色仍分别表示混沌和混合参数区域.由于来自吸引参数区域的迭代映射在动力平面上的轨道的复杂性,本文用更多不同灰度颜色表示相应参数的迭代映射在动力平面上的轨道条数并用数字组合“number1_number2”表示该区域参数可以构造几条(number1)几周期(number2)轨道的迭代映射.这样划分参数断面上的吸引参数区域以后,可以看到M集上吸引参数区域主要有3类不同的参数区域:1)迭代映射在动力平面上有1条或多条以原点为中心的周期轨道的参数区域.2)迭代映射在动力平面上有1条位于原点的1周期吸引轨道和多条吸引周期轨道关于原点对称分布,但每条吸引周期轨道的连线不通过原点的参数区域,如图5中的5:(1_1,4_2)参数区域，则表达了与该参数区域相对应的迭代映射在动力平面上共有5条吸引周期轨道，其中有1条位于原点处的1周期轨道和4条不过原点的2周期轨道.3)迭代映射在动力平面上有4条旋转对称分布的吸引周期轨道的参数区域,如果把图5中的M集形象地看成是1条“鱼”,这样的参数区域在“鱼尾”部分,其中的参数可用于构造动力平面上具有4条旋转对称分布的轨道.图5(b)是图5(a)中方框区域的放大图,值得注意的是这种参数区域内的不同参数下的迭代映射在动力平面上的迭代轨道的条数相同(4条),但旋转对称分布的轨道周期值随参数的变化而变化,并有倍周期变化的特点.如表1中参数c3在图5(a)中位于 “鱼尾”参数区域,从图4(a)可知,参数c3下的迭代映射在动力平面上有4条旋转对称分布的2周期轨道,从放大的图5(b)中可以看到,参数实际上位于由 “4_2”参数带分隔的4_2参数区域中.而位于“鱼尾”区域中的独立“小鱼”部分更是出现了4_2、4_4和4_8的4条轨道的参数区域,相应的迭代映射在动力平面上的4条旋转对称轨道的周期值随着参数模值的增大从2周期变化到4周期、再变化到8周期,并且每个区域中间被更窄的 “4_4”和“4_8”参数带分隔,其中为了看清“4_4和“4_8”隔离带的存在,本文用白虚线覆盖了代表“4”条轨道的隔离条带.需要说明的是这几条出现在鱼尾部的4_2、4_4和4_8隔离带是在加大了确定每个局部极值点轨道的周期值所需要去掉的瞬态(从3000次加大到10000次)后得到的(在3000次去瞬态的条件下,这些隔离带的参数下的迭代映射的轨道条数是8条).在图5(b)中的右上角附近8条吸引周期轨道区域由(4_1,4_3)参数区域和(4_1,4_6)参数区域组成；而在图5(b)的“小鱼”参数区域中的 “8_2”区域中的参数可构造出有8条、2套4旋转对称分布的2周期吸引轨道的迭代映射,当在λ参数轴上取参数,即ω取值为0时,相应的迭代映射在动力平面上有一套D4对称分布的8条2周期轨道.

图5 参数截面C上标明轨道条数和周期值的广义M集

4 构造非线性迭代函数系

图5所展示的广义M集为有效构造式(4)在动力平面上的混沌吸引子和充满Julia集提供了可选参数区域,同时,也为用式(4)构造非线性迭代函数系(NIFS)提供了可能.事实上,本文实现了通过在图5所示的广义M集的同一个吸引参数区域中选取参数构造迭代映射,进而构造NIFS,并生成了相应分形.本文所构造的NIFS形式上如式(5)所示:

(5)

其中: {α=-0.57087,β=1.30842,γ=-0.86886};ci=(λi,ωi)取自图5广义M集中同一吸引参数区域;k是迭代映射数量或所选参数数量;Xi是fci(z)在动力平面上的充满Julia集;X是k个迭代映射的充满Julia 集的公共吸引域.由于fci(z)在动力平面上的动力学特性随ci所在吸引参数区域的变化而变化, 具体的公共吸引域上分形的构造方法也是变化的.

4.1 广义M集上具有1条吸引周期轨道的参数区域

4.1.1 广义M集上1_1参数区域

观察图5广义M集中最大的吸引参数区域是1_1参数区域,在这个参数区域中任选一组参数(λ,ω)再结合固定参数{α=-0.57087,β=1.30842,γ=-0.86886}就构造出了一个如式(4)所述的动力平面上迭代映射,当选取2个以上这样的参数构造迭代映射并将这样的一组迭代映射定义为一个NIFS时,随机迭代的结果只是出现了动力平面上的原点,没有分形出现.图6表明:在1_1参数区域任选一个参数(λ,ω)=(0.905,0.286),相应的迭代映射在动力平面上的基本搜索区域里有5个局部极值点,这5个局部极值点的轨道都被吸引到了原点,因此,这个迭代映射在充满Julia集里面只有(0,0)点这一条吸引周期轨道.由式(4)可知,(0,0)点是所有1_1周期参数区域下的迭代映射的吸引不动点,因此,采用2组以上的参数(λ,ω)构造的迭代映射所定义的NIFS,当从其中的任意一个迭代映射的吸引不动点(0,0)(分形上的点)开始NIFS的随机迭代时,得到的下一个点永远是(0,0)点.结果表明这个参数区域中的参数不能用于构造有效的NIFS.

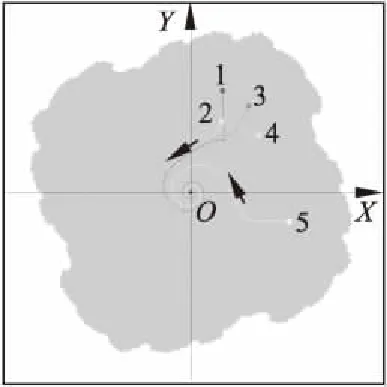
图6 1_1参数区域的充满Julia集及5个局部极值点轨道

4.1.2 具有1条高吸引周期轨道的参数区域

与图5中黑色参数区域相应的迭代映射在动力平面上有1条吸引周期轨道，这个参数区域表达为“1_number2”形式.在这些参数区域中选取2个以上靠得较近的参数就可以构造如式(5)所示的迭代函数系NIFS.在NIFS中,任选一个迭代映射的吸引周期轨道上的任意1个吸引周期点作为初始迭代点,通过随机挑选NIFS中的1个迭代映射,计算初始迭代点的迭代轨道上的新点；反复随机挑选NIFS中的1个迭代映射,计算出迭代轨道上的下一个点,得到平面上的完整分形.

图7是采用图5中1_8参数区域中的3个相邻参数(见表2)构造的NIFS在动力平面的公共吸引域中的分形,3个迭代映射的充满Julia集分别用不同灰度的颜色表示,图7(a)中的中心区域是这3个迭代映射的公共吸引域,公共吸引域上显示了这3个迭代映射各自的1条8吸引周期轨道,图7(a)中的3个迭代映射的轨道点之间的黑色集合是用本节方法得到的2套4旋转对称分布的分形,图7(b)是图7(a)中位于第1象限附近的方框中的2个局部分形的放大图,图7(c)和图7(d)是图7(b)的进一步放大图.图7说明参数选得靠近,其相应的充满Julia集的公共吸引域X几乎是每个迭代映射的充满Julia集Xi,由于各条轨道靠得很近,使得轨道点之间产生的分形集合非常小,局部放大后可见清晰的分形,注意到在公共吸引域中的完整分形是Z4对称分布的.

4.2 具有多条原点在吸引周期轨道连线内部的吸引参数区域

在图5所示的广义M集中,除了白色逃逸参数区域、深灰色混沌参数区域和浅灰色混合参数区域外,其余更多的不同灰度颜色代表的是吸引参数区域.除去黑色的吸引参数区域,其他区域代表的是一个迭代映射在动力平面上具有多条吸引周期轨道的参数区域,这样的参数区域分成2大类:具有多条原点(0,0)在吸引周期轨道连线内部的吸引参数区域和多条轨道围绕原点Z4旋转对称分布的参数区域.

在具有多条原点在吸引周期轨道连线内部的吸引参数区域中有2条周期轨道参数区域和4条周期轨道参数区域,如图中的2_4、4_4、2_6、4_6、2_8、2_16……这样的参数区域,由于相应参数下的1个迭代映射有2条或4条高吸引周期轨道,用这样的参数构造的NIFS并构造分形时,每个迭代映射的各条吸引周期轨道需要等概率地被选取,可以通过1个映射的多条轨道之间的几何对应关系来实现.由于迭代映射式(4)在动力平面上的图形具有Z4旋转对称特性,每个迭代映射的所有轨道上的所有周期点在动力平面上的分布也是Z4旋转对称分布的,因此,具有2条周期轨道的迭代映射,其2条周期轨道之间就具有90°旋转对称关系；而具有4条周期轨道的迭代映射,它的1条周期轨道通过旋转90°、180°和270°就可以与它的另外3条轨道重合.对于由具有2条周期轨道的迭代映射构造的NIFS,为了使具有这样动力学特性的迭代映射构造的NIFS式(5)能够生成具有Z4对称特性的分形,本文提出的方法是:选取任意一个迭代映射的任意一条轨道上的任意一个周期点作为初始迭代点,并随机将其进行0°或90°旋转；通过随机选取NIFS内的一个迭代映射计算出这个点的一个新点,对这个新点再次进行随机的0°或90°旋转,并通过随机选取NIFS内的一个迭代映射计算出这个点的下一个点,直至迭代到指定的迭代次数,得到NIFS在动力平面上的分形.当进行局部放大后,即可以得到清晰的局部分形.对于由具有4条周期轨道的迭代映射构造的NIFS,为了使具有这样动力学特性的迭代映射构造的NIFS式(5)能够生成具有Z4对称特性的分形,本文提出的方法是:每次采用一个随机选取的迭代映射计算下一个点之前,对当前点进行随机的0°、90°、180°或270°旋转,以保证4条周期轨道被等概率地用到,其他迭代过程同具有2条周期轨道的NIFS一样进行.

图8是采用图5中2_8参数区域中的2个相邻参数(见表2)构造的NIFS在动力平面公共吸引域中的分形,2个迭代映射的充满Julia集分别用不同灰度颜色表示,图8(a)和图8(b)分别是迭代映射fc1与迭代映射fc2的充满Julia 集和其上的两条8吸引周期轨道；图8(c)中的浅灰色是这2个迭代映射的公共吸引域,其上显示了这2个迭代映射各自的2条8吸引周期轨道以及相应的分形,图8(d)放大显示了图8(c)框中Z4旋转对称分布的局部分形图；图8(e)-图8(h)进一步放大了图8(d).

在迭代映射具有多条原点在吸引周期轨道连线内部的吸引参数区域中还有轨道条数为奇数的参数区域,如图5中所示的3_8、3:(1_1,2_2)、5:(1_1,4_2)、3:(1_4,2_20)、5:(1_4,4_8)等吸引参数区域.由于迭代映射式(4)的Z4对称性,这些参数区域对应的迭代映射在动力平面上可能有多条相同的轨道周期值(3_8)(其中的2条8周期轨道之间具有90°旋转对称),也可能有不同的轨道周期值3:(1_1,2_2)或3:(1_4,2_20).当用选取2个以上参数的迭代映射构造一个NIFS时,NIFS的分形可以用NIFS中的1个迭代映射的2_number2或4_number2的1条轨道上的1个周期点作为初始迭代点进行随机迭代,并对其每一步得到的新点进行随机的(0°或90°)或(0°、90°、180°或270°)旋转,对其进行NIFS中的迭代映射的随机迭代,构造出相关的分形；用另一条与其他轨道不具有旋转对称关系的周期轨道上的周期点作为一个初始点,对NIFS实施4.1.2所述的单条吸引周期轨道的迭代映射之间的随机迭代方法,生成分形.因此,用这种具有奇数条轨道的迭代映射构造NIFS时,1个NIFS可以生成2个分形,需要用不同的周期轨道上的初始点分别迭代得到.图9是采用图5中3:(1_4,2_20)参数区域中的2个相邻参数(见表2)构造的NIFS在动力平面上公共吸引域中的分形.2个迭代映射的充满Julia集分别用不同灰度颜色表示,在公共吸引域中分别表示了2个迭代映射的1条4周期轨道和2条20周期轨道.图9(a)中给出了在公共吸引域上用每个迭代映射的2条20周期轨道生成的分形；图9(b)是在公共吸引域上用每个迭代映射的1条4周期轨道生成的分形；图9(c)和图9(d)分别是其相应的分形放大图.

图8 来自2_8参数区域的2个迭代映射的分形

图9 来自3:(1_4,2_20)参数区域的2个迭代映射的分形

当选用2个以上来自3:(1_1,2_2)或5:(1_1,4_2)吸引参数区域的参数构造NIFS时,由于4.1.1节所述的原因,这样的NIFS只能生成由每个迭代映射的2条2周期轨或4条2周期轨随机迭代的分形.图10是用图5中3:(1_1,2_2)吸引参数区域的参数c2与附近的另一个参数(见表2)构成的迭代函数系(5)在2个充满Julia集的公共吸引域上生成的分形及放大图.

4.3 具有Z4旋转对称轨道的参数区域

如果称图5中的广义M集是一条“鱼”,则在鱼尾处的参数区域的参数可以构造出在动力平面上具有关于原点的Z4旋转对称分布的4条轨道的迭代映射.与前述的其他可以构造具有4条轨道的迭代映射的参数区域不同,这个参数区域的相应迭代映射在动力平面上的每条轨道连线的内部区域不包含原点.“鱼尾”参数区域下的迭代映射的轨道周期值从1变化到2,即有4_1和4_2参数区域；在参数λ轴附近的“小鱼”内,有4_2、4_4和4_8参数区域.在这些参数区域里选用2个以上的参数构造出的NIFS,其分形的构造方法与前述4_4、4_6等吸引参数区域的NIFS的分形构造方法一样:选用NIFS中任意一个迭代映射中的一条周期轨道上的一个周期点作为初始迭代点,对其进行随机的(0°、90°、180°或270°)旋转,随机选用NIFS中的一个迭代映射,计算出初始迭代点的下一个新点,并重复前述迭代过程,直至迭代到指定的迭代次数,得到NIFS的公共吸引域上的分形.

图10 来自3:(1_1,2_2)参数区域2个迭代映射的分形

图11是采用图5中“鱼尾”处的4_1参数区域中的3个相邻参数(见表2)构造的NIFS在动力平面上公共吸引域中的分形,3个迭代映射的充满Julia集分别用3个不同灰度颜色表示,图11(a)中的浅灰色是这3个迭代映射的公共吸引域,公共吸引域上显示了这3个迭代映射各自在4旋转对称分布的分形上的4个1周期不动点,图11(b)是位于第1象限的局部分形的放大图.

图11 来自4_1参数区域的3个迭代映射的分形

观察图5(b),在“鱼尾”的右上方有8:(4_1,4_3)和8:(4_1,4_6)参数区域.用这样参数区域的参数构造出的1个迭代映射,在动力平面上有两套Z4旋转对称分布的吸引周期轨道,因此,在这个参数区域中选取2个以上的参数构造NIFS时,这个NIFS对应着2个分形.分形的构造方法是选用NIFS中一组Z4旋转对称分布轨道的任意一个迭代映射中的一条周期轨道上的一个周期点作为初始迭代点,对其进行随机的(0°、90°、180°或270°)旋转,随机选用NIFS中的一个迭代映射,计算出初始迭代点的下一个迭代点,并重复前述迭代过程,直至迭代到指定的迭代次数,得到NIFS的公共吸引域上的一组Z4旋转对称轨道下的1个分形；通过选用NIFS中另一组Z4旋转对称轨道的任意一个迭代映射中的一条周期轨道上的一个周期点作为初始迭代点,重复前述过程,得到NIFS的另一个分形.

图12是用图5(b)中8:(4_1,4_3)参数区域的2个相邻参数(见表2)构成的NIFS在2个充满Julia集的公共吸引域上分别用2个映射的4个旋转对称分布的1周期不动点轨道(图12(a))和4个旋转对称分布的3周期轨道(图12(b))生成的2个分形及放大图.

在λ轴附近的“小鱼”吸引参数区域中嵌套着3块8_2参数区域,在这些区域中每一个参数都对应着一个具有8条2周期轨道的迭代映射,这8条轨道组成了2套Z4旋转分布的2周期轨道,参数区域中采用2个以上的参数构造的NIFS,可以用构造图12的方法得到2个分形.值得注意的是:如果在λ轴上选取2个以上的参数可以构造出由以D4对称方式分布在动力平面上的8条2周期轨道的迭代映射构成的

图12 来自8:(4_1,4_3)参数区域的2个迭代映射的分形

图13 来自λ轴上8_2参数区域的2个迭代映射的分形

NIFS.此时,从NIFS的任意一个迭代映射的8条轨道的任意一个周期点作初始迭代点,并将点进行{I、R90、R180、R270、F、R90∘F、R180∘F或R270∘F}的D4对称点的随机选取,随机选用NIFS中的一个迭代映射,计算出该点的下一个迭代点,并重复前述迭代过程,直至迭代到指定的迭代次数,将得到NIFS的公共吸引域上一个具有D4对称的分形,其中I是2维单位矩阵、R90是围绕原点的90°旋转矩阵、F是关于X轴的反射矩阵.图13是在λ轴上选取2个参数(见表2)所构造的NIFS在其公共吸引域上2套8条2周期轨道和相应的分形(图13(a))及其第一象限的分形放大图(图13(b)).

表2 构造图7-图13的参数

Table 2 Construct the parameters of fig.7 to fig.13

图号参数ci=(λi,ωi)7c1=(0.944,0.822),c2=(0.947,0.809),c3=(0.957,0.800)8c1=(1.008,0.908),c2=(1.032,0.913)9c1=(0.338,1.514),c2=(0.337,1.506)10c1=(-0.670,0.523),c2=(-0.669,0.482)11c1=(1.437,0.493),c2=(1.422,0.539),c3=(1.422,0.593)12c1=(1.475,0.629),c2=(1.478,0.630)13c1=(1.480,0.000),c2=(1.494,0.000)

5 结束语