一种改进节点凝聚度的密度峰值聚类算法
2020-07-13吴辰文魏立鑫刘晓光
吴辰文,魏立鑫,刘晓光
1(兰州交通大学 电子与信息工程学院,兰州 730070) 2(兰州交通大学 电子与信息工程学院 计算机应用技术,兰州 730070) 3(兰州交通大学 电子与信息工程学院 软件工程,兰州 730070)
1 引 言
在数据挖掘领域中,聚类是一种无监督的学习方法,其目的就是将含有杂乱无章数据的集合分为若干簇,并且使簇中的数据尽可能相似,簇间的差别尽可能大[1],以便为我们提供有价值的信息.聚类分析在模式识别、医学、数据挖掘、图像识别等领域有着广泛的应用.
根据聚类原理将这些算法分为5类:基于划分的聚类算法(K-Means,Fuzzy C-Means等)、基于层次的聚类算法(Clustering Using Representative,Chameleon等)、基于网格的聚类算法(MAFIA,STatistical INformation Grid等)、基于密度的聚类算法(Density-Based Spatial Clustering of Applications with Noise,Ordering Points to Identify the Clustering Structure等)和基于模型的聚类算法(Self-Organizing Maps,Expectation-Maximization Algorithm等)[2-7].除了这些经典的算法之外,于2014年在《Science》学术期刊中发表了一种新的密度峰值聚类算法[8](Density Peaks Clustering,DPC)引起了广泛的关注.
DPC算法的核心思想是寻找被低密度区域划分开的高密度区域.利用局部密度ρ和不同簇高密度点之间的距离指标δ来生成“决策图”,并选取异常大的ρ、δ值作为类簇中心,将剩余数据点分配到已选取的类簇中心,直至完成数据点的分配.该算法具有简单高效、发现任意形状簇、样本归类无需迭代、参数设置少等优点,但是该算法规定每个簇中必须有密度最大的点作为簇中心,当数据分布不均或同一簇含有多个高密度点,很容易将一个簇分为几个子簇.近些年来,很多学者对密度峰值聚类算法进行了一些改进,并且也取得了一些研究成果,包括对聚类中心判断、经验截断距离dc的选择、密度计算方法改进等问题[9].例如,Ma C等[10]在文中指出,按照给定的评价指标对数据点排序,选取前m个最大值作为聚类中心;Wang S等[11]在基于信息熵的基础上提出一种自动获取截断距离dc的方法,但是时间成本会增大;高诗莹等[12]利用样本的密度比,避免丢失低密度的簇,从而提高聚类效率;Zhang W,Li J[13]将DPC算法与Chameleon算法结合,避免了将一个簇分为几个子簇的情况,但是时间复杂度高达O(N2+NlbN+NM);Du M等[14]采用Principal Components Analysis方法对高维数据点降维,然后利用K-Nearest Neighbor思想估计密度,提高了对高维数据的处理能力.
从上面的研究可以知道,密度峰值聚类算法有很多的改进算法.数据点在不同类别中密度差值太大,或者在具有多个类簇中心的同一类别中密度差值太小,这些条件都会影响最终的聚类结果.目前DPC改进算法的文章很少考虑上述两个要素,而且点与点之间的相互关系不明确,但是在本文研究中,很好的兼顾了上述情况.针对密度峰值聚类算法(Density Peak Clustering,DPC)处理密度分布不均匀的数据集或在同一簇中有多个高密度点的情况,难以准确选取聚类中心,很可能将同一个簇划分为若干个子簇.本文提出一种改进节点凝聚度的密度峰值聚类算法(Improved Aggregation Density Peak Clustering,IA-DPC).首先,将要数据转换为加权完全图,由于完全图是每对顶点之间恰有一条边的无向图,可以看做是一个完全连接的无权网络,采用不同的加权方式对完全图进行加权,形成加权完全图.其次,利用网络中改进节点凝聚度的思想构建数据节点的重要度的评价函数,对节点局部重要度进行计算并排序.然后,选取重要度与距离乘积异常大的点作为类簇中心.最后,将剩余点进行分配直至完成.经过一系列的实验仿真,研究表明该算法在密度分布不均匀及有多个高密度点的数据集中具有更准确选取聚类中心的能力.
2 密度峰值聚类算法与改进节点凝聚度
在整个研究工作开始时,定义数据集为U={vi},i=1,2,…,N,vi表示数据集中的任意数据点,将数据集转化为加权完全图,因为加权完全图能更好的反映节点间的紧密度,而且也能很好的表达其中的结构.在整个无权图向加权图的转化中,应该考虑图的相异权值和相似权值问题[15],相异权表示权值越大,点之间距离越大,反应它们之间的关系越疏远;相似权表示权值越大,点之间距离越小,反应它们之间的关系越紧密.本文采用相异权的方法给图赋予权值,由于该图是加权完全图,所以可将它看作完全连接的加权网络,假设vi是网络G=(V,E)中的任意一节点.需要对每个数据节点定义两个指标:1)vi节点重要度评价指标ui;2)节点vi与比vi有更高重要度的节点间距离δi.
2.1 密度峰值聚类算法原理
对于数据集U中的任意数据点vi,DPC算法都要求计算数据点的两个属性值:局部密度ρi和与高密度点间的距离δi.根据上述两个属性值来确定DPC算法的聚类中心.
定义局部密度ρi:
(1)
其中:当x<0时,函数χ(x)=1;当x≥0时,函数χ(x)=0.dij表示数据点vi与vj之间的欧式距离,dc表示截断距离,可以由用户设置,一般情况下,在所有数据点的距离值从小到大排序后,首先选取距离值个数的1%~2%,然后选择其中最大的一个距离值作为截断距离dc.x表示节点之间的距离值dij与截断距离值dc之差,j表示除了节点vi以外的任意节点.等式(1)表明,截断距离的选取会影响DPC算法的局部密度.当样本较小时,使用核算法来计算样本的局部密度[16],这种方式可以避免截断距离对样本局部密度甚至聚类结果的影响.表达式如下:
(2)
定义距离值δi:
(3)
其中:如果δi越小,dij也就越小,因此点vi和vj可能在同一簇中;当δi越大时,dij也就越大,vi与vj越不可能为同一类.对于具有高密度的点,通常使用δi=maxj(dij)来表示点间距离,需要保证高密度点之间的距离是最大的.如果一个点的δi值大于其最近邻点距离,那么就认为该点是聚类中心.
文献[8]指出,可以通过上述公式计算局部密度ρi和距离δi绘制决策图.横轴表示局部密度,纵轴表示距离.根据聚类中心的特点,在决策图中选择局部密度和距离异常大的点作为聚类中心.但是,在确定聚类中心的过程中,包含有许多的主观因素,不同的用户可能通过在决策图上不同的选择,得到不同的聚类结果,尤其对于密度分布不均匀的数据集,很可能会发生将同一簇划分为若干簇的情况.
2.2 改进的节点凝聚度
在网络G中,一个节点的凝聚度是依据节点的收缩情况而定.节点收缩是指将vi相连接的k个节点收缩成一个新的节点v′i并用v′i表示这k+1个节点.vi节点以最短路径收缩于v′i,如果新节点对整个网络至关重要,那么整个网络在节点收缩后可以更具好的凝聚在一起.
为了更清楚的理解凝聚度的概念,文献[17]给出了网络凝聚度的定义,用节点间最短距离的算术平均值L与节点总数目N乘积的倒数来表示凝聚度.
定义网络G的凝聚度:
(4)
其中:要求节点总数N≥2,dij表示数据点vi与vj之间的距离.当N=1时,凝聚度∂的取值为1.
定义节点重要度为:
(5)
其中:G*vi表示节点vi收缩以后的网络.∂(G*vi)表示节收缩以后的网络凝聚度.
通过式(4)、式(5)可以得到节点重要度为:
(6)
其中:ki表示与vi相连接的k个节点.
因此,从式(6)中看出,vi的重要度与vi在整个网络中的位置相关.连接度指从一个节点出发到另一个节点,最短距离经过该点边的数目,如果一个节点的连接度很大并且位置很重要,则节点收缩后的网络的凝聚度也会变大.所以,可以认为该节点在整个网络中比其他节点更为重要.
凝聚度的定义适合于无权网络.当该定义用于加权网络时,它会受不同权重的影响.点权表示与节点i关联的边权之和,由于该网络是无向网络,边权赋值方式为相异权,则点权应该表示为边权倒数之和.所以对于加权网络,应该重新定义加权网络节点的重要度.文献[18]重新定义了加权网络的凝聚度:
(7)
其中:W(G)表示加权网络中所有点权相加的平均值,L(G)表示在加权的路径前提下加权网络变为无权网络后的平均最短距离,重新定义后的网络凝聚度为:
(8)
其中:Mi表示与节点i相关联的节点总数目,ωij表示与节点i相连的边权.等式(8)中,要求节点数N≥2,dij表示vi和vj在加权路径下的无权距离.当节点数目N为1时,凝聚度∂(WG)的取值为1.
定义节点vi的重要度:
(9)
其中:WG′表示在加权网络下节点i收缩以后的网络.根据式(8)、式(9),点与点连接的紧密度越高,点权和的平均值就越小.在相同条件下,网络凝聚度越高,定义的节点重要度就越高,那么这个点的就会显得比其他点更加重要.
上述对加权网络节点重要度的描述仅仅只考虑了点权.在某些情况下,边权很大程度上也会影响节点的重要度.因此,文献[19]提供了一种使用边代替加权网络中节点的方法,将边与边连接关系作为点,将网络G转化为G*.当边权重的差异度消失时,加权网络将转化为无权网络,如图1~图2所示.
G*是用节点替代边后的网络,可以通过计算该网络中节点的凝聚度来替代边的凝聚度,为了综合考虑两种情况,将在网络G中vi的重要度和在网络G*中vj的重要度相加,得到:
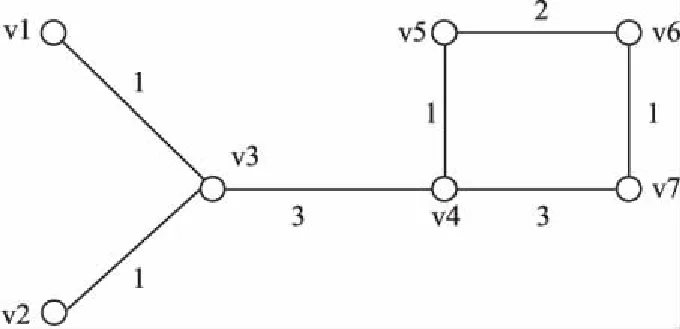
图1 网络G

图2 网络G*
(10)
其中:IMCn表示在网络G中任意节点vi的重要度,IMCe表示在网络G*中任意节点vj的重要度,α表示点权权重系数,β表示边权权重系数,T表示在G*中的节点数.为了避免节点重要度值的差异度过大,进行归一化处理:
(11)
令γ=α/β且α+β=1,γ表示点权与边权的比例系数.要依据实际情况,进行比例系数的调节.γ的取值与点重要度和边重要度都相关,也就是说比例系数与G和G*都相关.在G和G*中,利用图论中度的概念设置比例系数.
(12)
由于该比例系数的确定也带有一定的主观性,所以通过α+β=1可以相互适当地进行调节.在调节过程中,适当扩大α取值范围,在(0,1)范围中,用原α值加上几个差异不是很大的数,调整α后对得到的多个α值求平均值,利用α+β=1计算出β,进而求得不同的γ值.
2.3 基于改进节点凝聚度的密度峰值聚类(IA-DPC)
在IA-DPC算法中,先将数据集转为加权完全图,把数据点作为节点,通过计算两个节点之间的距离作为两点之间的边权重,进行存储.将节点的点权与该节点相连的边权和作为网络节点总权值,并用改进节点凝聚度方法评估每个节点的重要程度.类簇中心的局部重要度高于周围邻居,具有较高重要度的节点间距离更大.对节点重要度进行排序,比较选取重要度ui和距离δi乘积的异常大点作为类簇中心.选取类簇中心后,将剩余点进行分配,得到最终的聚类结果.
IA-DPC算法具体步骤:
Step 1.数据归一化并初始化变量dc、γ,将数据转化为加权完全图G;
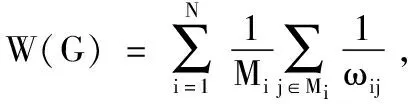
Step 3.计算vi(i=1,2,3,…,N)节点收缩后网络G′的平均无权最短距离L′和平均点权和W′;
Step 4.计算G′的加权凝聚度,并计算G中节点的重要度IMCn(当G转化为G*后,计算G*中边转化为节点后的重要度IMCe);
Step 5.将G转化为G*,重复Step 2~Step 4;
Step 6.调节比例系数γ,计算数据点重要度IMC(vi),并对其进行排序;
Step 7.比较选取重要度ui和距离δi乘积异常大的点作为聚类中心;
Step 8.分配剩余数据点到相应最近的类簇中心,完成聚类.
从上述算法步骤中,可以知算法的主要复杂度集中在对加权图之间转化、节点重要度的计算和数据遍历的计算.由于算法是构造的完全图,复杂度至少是O(n2),为了计算网络G中的节点凝聚度,其核心的计算部分复杂度为O(n3),由于必须考虑网络G*中的复杂度,转换后的网络与原网络具有相同的计算复杂度.那么G与G*的复杂度是一样的.对于数据的遍历,采用用邻接矩阵进行存储,由于矩阵中元素数量为n2,其复杂度为O(n2).就整体性能而言,算法的复杂度在O(n3)的数量级上.
3 实验仿真与结果分析
选择5个人工数据集和4个真实数据集来验证IA-DPC算法性能.选用聚类算法常用的两个指标F-measure和ARI对算法性能进行评估.同时,给出两种比较算法(DPC,ADPC-KNN[20]).具体数据集及其特征如表1所示.
在所有算法中,三种算法都有设置参数的情况,DPC需要设置截断距离dc,通过决策图需要手动选取聚类中心,ADPC-KNN该算法需要设置k近邻的个数,对于IA-DPC算法需要调节比例系数γ及截断距离dc的设定.在IA-DPC算法中根据γ的调节方式选取效果最好的聚类结果进行展示.DPC和IA-DPC截断距离dc值都是选取所有数据点中距离值个数排序的1%~2%处距离值的平均值.经过算法在数据集上的多次实验,选择结果最佳的图形展示.
表1 实验数据集
Table 1 Experimental datasets

DatasetInstancesDimensionsClustersCompound39926Aggregation78827Banded_d51234Scatter1000100034D313100331Iris15053Wine178143Glass214106CellCycle_384384175
3.1 聚类结果分析
图3~图4显示了9个数据集中的两个数据集在算法(DPC,ADPC-KNN,IA-DPC)上的聚类结果.实验数据集在MATLAB 2014a版本的win10环境中运行.硬件配置为4G内存和2.6GHz主频.

图3 D31数据集
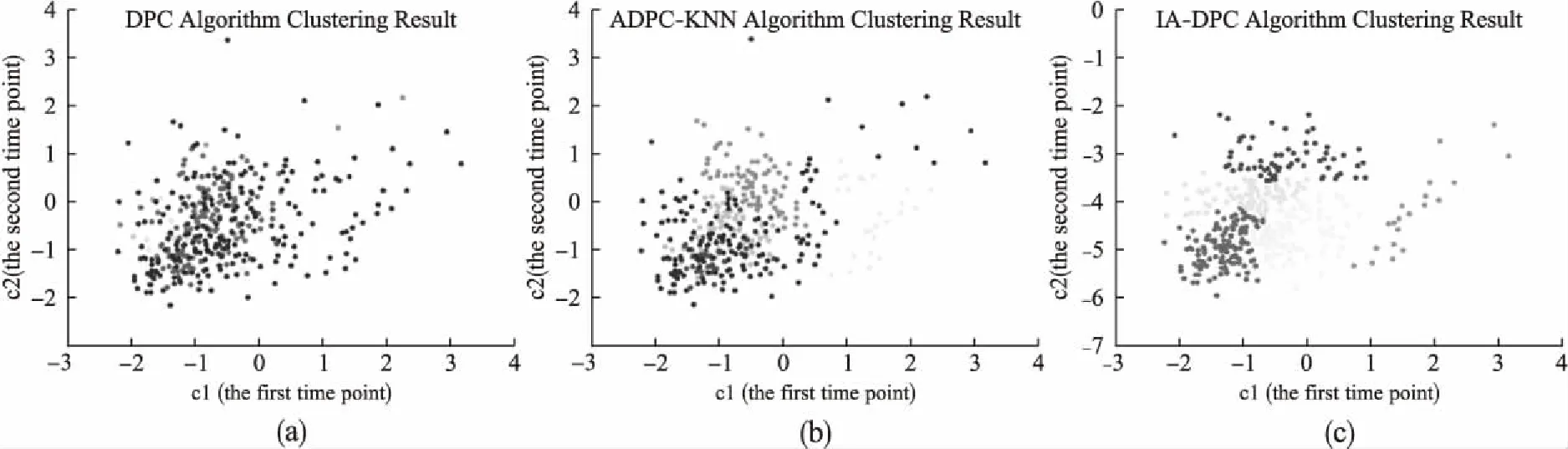
图4 CellCycle_384数据集
首先,使用人工数据集进行实验验证,包括Compound数据集、Aggregation数据集、Banded_d数据集、Scatter1000数据集和D31数据集.
如图3所示,显示D31数据集在三种算法中的聚类结果.可以看出三种算法都出现了错误聚类的情况.DPC算法和ADPC-KNN算法都不能划分某些簇.IA-DPC(γ= 0.752)算法在对某些点的划分上也不清楚,并且在该数据集上难以区分边界点.
接下来,使用真实数据集进行实验验证,这些数据集来自UCI,包括Iris数据集,Wine数据集和Glass数据集.还使用了一个酵母菌Gene数据集进行实验,实验结果如下:
CellCycle_384数据集[21,22]用于观察细胞中基因转录水平的周期性变化.它是具有先验知识的数据集.从全基因组中选择总共384个基因,将同一时刻达到转录峰值的基因作为一个标准类.
如图4所示,显示CellCycle_384数据集在三种算法中的聚类结果.在所有酵母菌转录水平的17个时间点中,选择第一个时间点和第二个时间点作为水平轴和垂直轴.从聚类可视化结果可以看出DPC算法的聚类结果效果较差.ADPC-KNN算法虽然能够识别几个类,但是直观上效果依然不是很好.对于IA-DPC(γ=1.500)算法能够识别出5个类别.
3.2 算法指标分析
为了分析聚类结果的差异性,在聚类中选择了两个指标进行结果分析:调整后的兰德指数(ARI)和F-measure(F1).ARI和F1的值越大,就越接近真实的聚类效果.同时,表2、表3分别列出了聚类结果下的F1和ARI的值.IA-DPC算法在这9个数据集的聚类过程中,γ取值会对重要度产生影响进而对该聚类算法聚类性能产生影响,用更直观的可视化展示其影响结果.
表格中的黑体数据表示最优值.F1结果显示在表2中,可以看到IA-DPC算法在一些数据集中具有低的F1值,但是相较于其他两个算法,本文算法总体上优于其他两个算法.ARI结果显示在表3中,从表3可以看出,IA-DPC算法在这些数据集中相较其他两种算法,该算法几乎都具有最大的ARI值.为了方便直观的判断,对表格中的数据集进行可视化.
表2 F-MEASURE指标
Table 2 F-measure index

AlgorithmsDatasetsCompoundAggregationBanded_dScatter1000D31IrisWineGlassCellCycle_384DPC0.7710.8120.7940.9600.9120.9520.8530.5250.475ADPC-KNN0.9020.9751.0000.8810.9550.9380.8100.8100.690IA-DPC0.8890.9381.0000.9480.9700.9400.9310.8270.899
表3 ARI指标
Table 3 ARI index

AlgorithmsDatasetsCompoundAggregationBanded_dScatter1000D31IrisWineGlassCellCycle_384DPC0.7370.7540.7800.8260.8790.8780.5440.382-0.020ADPC-KNN0.8420.8751.0000.7610.9240.8300.5030.4930.393IA-DPC0.8550.8311.0000.8540.9470.8780.6100.5580.779
根据表中数据,可视化F1值、ARI值分别如图5、图6显示,在人工数据集方面,IA-DPC算法具有更高的性能,或与其他两种算法的性能几乎相同.但在真实数据集方面,IA-DPC算法优于其他两种算法.

图5 F1指标
同时,如图7所示,在IA-DPC算法中,根据调节比例系数的方法最终得到三个γ值,通过在算法中的比较,可以看出不同数据集的最优γ值是不同的,并且可知比例系数越大,节点凝聚度也就越大,对区分聚类中心和其他节点的重要程度影响也就越大.因此,IA-DPC算法在实际应用中具有特定的参考价值.
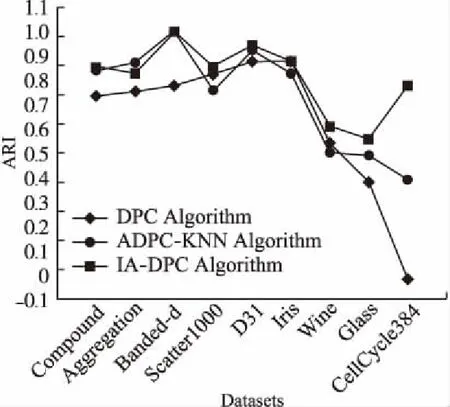
图6 ARI指标
4 结 论
在本研究中,针对密度峰值聚类算法在密度分布不均匀的数据集中难以产生良好的聚类效果,提出了一种改进策略的算法.在实验数据集的验证中,IA-DPC算法在处理密度分布不均匀的数据集时具有一定的优势,能够提高DPC算法的聚类效率,从而更加准确的聚类.但是该算法也需要一定的参数设置,有人为因素的影响,并且该算法时间复杂度高,核心算法时间复杂度高达O(n3),对于处理高维数据,效果不理想.在以后的研究中,重点会放在解决高维数据聚类方面.

图7 比例系数γ
