三支决策视角下的云平台负载预测研究
2020-07-13姜春茂李志聪
杨 阳,姜春茂,李志聪
(哈尔滨师范大学 计算机科与信息工程学院,哈尔滨 150025)
1 引 言
在云计算技术迅速发展的大背景下,云平台已然成为各大企业和运营服务提供商的战略性平台,它提供了一个高度可扩展和按需处理的服务.然而,由于大量的用户动态的访问云环境,云服务提供商需要及时分配资源,这使得静态的分配物理资源存在诸多问题.根据负载需求进行云资源分配时,存在按照过多分配会导致资源利用率降低,过少分配会导致违反SLA协议的现象[1].因此,云计算中的负载预测是资源管理优化的重要组成部分,能预测到未来一段时间的资源使用情况,可以有效地管理资源,实现资源利用最大化.预测技术由来已久,随着云计算的快速发展,如何进行虚拟资源的有效管理成为一个关键问题,将预测技术融入到云资源管理中势在必行,引起了众多专家学者对此进行研究,也涌现出诸多研究成果.Calheiros Rn等人提出一个基于自回归移动平均模型(ARIMA)的云负载预测模型[2],该模型是广泛使用的一种时间序列预测模型,但它不能有效地捕获时间序列数据中的非线性模式.Gupta S利用深层双向BLSTM神经网络对云资源使用情况进行预测,它能够学习长期依赖,记住长时间段的信息,被明确用来解决长期负载预测问题[3].Sheng D提出一种基于贝叶斯模型的预测方法来预测长期时间区间内以及未来连续时间区间内的平均负载,但它仅仅能预测平均负载,而无法捕获负载波动[4].Duy等人使用反馈人工神经网络预测节点负载,其基于自回归模型的ANN模型具有较强的非线性泛化特性,可捕获到输入值与输出值间潜在的关联关系,但却不能很好地预测节点的固定时间间隔的长期负载[5].Yang等人基于进化算法(EA-GMDH)与相空间重构模型(PSR),提出了一种新的预测模型,它与ANN模型一样,不能很好地利用长期的历史数据,从而限制了其进行多步预测的能力[6].基于此,本文提出了基于三支决策的云资源负载预测模型,来有效地解决传统预测模型无法兼顾平缓期和抖动期的负载预测问题.
三支决策理论[7]是加拿大学者姚一豫教授为了对决策粗糙集中三个域提供一种合理的语义解释,提出的一种符合人类认知的信息处理模式和有效的复杂问题求解策略.根据粗糙集中一对阈值α和β将整个论域划分到三个不同区域:正域、负域和边界域,三支决策给出了一种语言规则解释,将这三个域分别表示接受、拒绝和延迟决策(不承诺).它的基本思想是以“三”作为思考,是一种蕴含一分为三,三分而治的认知模型.云计算系统的组成要素中存在着众多的三支要素,如按照作业的时间可以分为长、中、短;针对虚拟机则涉及到合并、迁移、关闭的三种操作;针对主机则涉及到激活、休眠、关机三种状态.借鉴三支决策基本思想,本文将三支决策引入云资源负载需求预测研究中,提出基于三支决策的云资源负载预测模型.
大量实际的云平台历史运行数据显示,云数据中心的负载呈现准周期效应.根据分析负载特征变化,本文借鉴三支决策的基本思想,通过引入中间域延迟决策的方法,使得整个论域划分成三个两两不相交部分.使得具有充分把握接受或者拒绝的对象集合直接判定为正域或负域,分别记为负载平缓期和负载抖动期,而信息相对不确定的对象集合则作为延迟决策区域等待进一步区分,记为负载波动期.而三个阶段的划分则根据相邻点均方根误差的计算.本文实验采用真实的云平台历史数据Google cluster trace,实验结果显示,相比于ARIMA,NN算法,DMASVR-3WD模型有着更小的违约率(SLA)和更高的准确率.
本文组织及结构如下:第二节综述了三支决策模型以及在两种时期下的预测模型.第三节提出基于三支决策的云资源负载预测模型(DMASVR-3WD)和基于代价评估的阈值确定方法.第四节给出实验分析结果.最后得出相关研究结论.
2 相关工作
2.1 三支决策模型
三支决策是一种符合人类认知的三分而治模型,通过一对阈值(α,β)可以将一个全集U划分为3个独立的区域.传统的二支决策往往只考虑接受和拒绝两种选项,但是在实际情况中,由于信息的不确定性或者不完整性,常常无法直接作出判断.此时,人类往往会自发的运用一种三支策略,将仅包含接受和拒绝二支决策理论拓展为,包含接受、拒绝和不承诺的三支决策理论.通过将整体区域一分为三,然后根据不同部将复杂问题分的特点有针对性的施加不同的策略,即将复杂问题利用分治策略转化为简单问题,在此基础上,姚一豫教授提出三支决策理论的基本框架,如图1所示.
三分而治是一种符合人类认知的问题处理策略,是一种有效的决策和信息处理模式,其广泛应用吸引了大批专家学者对此展开研究,产生了众多的研究成果,并成功应用于多个学科领域.胡宝清教授在总结几类具有代表性的三支决策模型的基础上,提出三支决策空间问题[8];姚景涛教授提出了三支博弈论[9,10];祁建军、魏玲等人提出三支概念分析理论[11-13];刘盾、梁德翠等人提出了三支决策的时空性以及三支决策的直觉模糊集理论[14,15];于洪教授提出了三支聚类[16,17];姜春茂教授提出了一种基于移动的三支决策模型有效度量方法[18,19].目前,三支决策理论也应用到云计算系统研究中.Jiang等人采用三支聚类算法,解决了负载敏感的云任务调度问题[20].云计算系统中存在众多的三支要素,在云资源预测中,也常常出现这种三支的情况,为实现精准有效的预测,对负载特征进行分析,可以将其分为负载平缓期、负载抖动期和负载波动期.从三支决策的角度来思考,即接受、拒绝和延迟决策.用户资源需求在某些阶段不能直接确定其属于负载抖动期或是负载平缓期,这时将资源需求情况强行二划分,在往下的预测过程中,可能会造成更大的违约代价.此时本文将这些不确定对象放入边界域,通过进一步的信息处理再进行决策更显得合理.

图1 三支决策模型
本文基于三支决策的思想,来进行云资源负载预测的三支划分:正域(POS)、边界域(BND)和负域(NEG),分别表示云资源需求确定属于负载平缓期的,不确定是否属于负载平缓期(或负载抖动期),确定不属于负载平缓期的(即确定是负载抖动期).
2.2 负载平缓期预测模型
二次移动平均模型(Double Moving Average,DMA)[21]是一种常见并且有效地时间序列分析方法.对于训练样本集合:{(xi,yi)},i=1,2,…,n.其中xi表示输入数据,yi表示输出数据.假设xt,xt-1,…,xt-(w-1)为某时刻t的长度为w的资源需求历史数据序列,如图2所示.

图2 滑动窗模型
即从时刻t-(w-1)到t的滑动窗包含的数据为[xt-(w-1),xt-(w-2),…,xt],因此定义t时刻对资源需求值的一次移动平均值为:
(1)
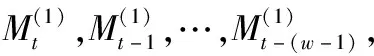
(2)
在t+T时刻的资源需求预测值yt+T,由时刻t的资源需求值at和T时间间隔内增量bt决定,即:
yt+T=at+bt·T
(3)
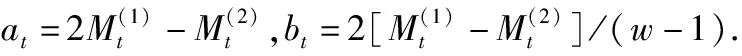
因此基于二次移动平均法,对t时刻历史资源需求序列进行分析,可以得到在t+T时刻的资源需求预测值:
(4)
不难发现,DMA模型更加适用于相对平稳,线性的时间序列预测,难以应对具有突发性变化的预测.
2.3 负载抖动期预测模型
支持向量回归算法(Support Vector Regression,SVR)[22]是在支持向量机算法(SVM)[23]的基础上,引入了ε不敏感损失函数,通过使用支持向量机拟合曲线,实现回归分析,从而将支持向量机从分类推广到了回归中.ε-不敏感损失函数可以保证误差函数有一定的界限,实现更强的鲁棒性.
根据风险最小化原则,对于训练样本集合:{(xi,yi)},i=1,2,…,n.其中xi表示输入数据,yi表示输出数据.给出SVR模型如下形式化定义:
f(x)=ωξ(x)+b
(5)
其中,f(·)表示预测值,ξ(·)表示非线性映射函数将输入数据映射到高维特征空间,x表示输入数据集合,ω表示权值,b表示偏置值.
为了实现更好的数据拟合效果,可以引入惩罚系数C,将该问题转化为如下优化问题:
(6)
约束条件为:
(7)
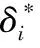
为了保证SVR算法的输入输出数据集之间的整体误差最小,权值向量ω表示为:
(8)
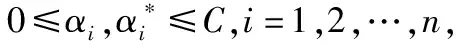
SVR通过将数据从低维空间映射到高维空间,在核空间里进行线性学习,从而实现回归拟合分析.引入核函数,得到如下回归函数:
(9)
其中,K(xi·xj)表示核函数.
核函数是SVR模型的关键所在,常见的核函数多项式核函数、有线性核函数以及径向基(RBF)核函数等,本文将RBF核函数引入SVR模型中,其形式化如下:
K(xi,xj)=exp(-γ‖xi-xj‖2),γ>0
(10)
不难发现,相比较一些传统的线性预测方法,SVR模型更加适用于非线性、非稳定的时间序列的预测,在对具有突发性变化的负载预测具有很好的效果.
3 基于三支决策的云资源负载预测模型
在本节中,基于云负载特征变化,提出一种云资源需求状态三分的预测模型—基于三支决策的云资源负载预测模型(DMASVR-3WD),并给出了一种基于代价评估的阈值确定方法.
3.1 云计算资源预测系统
云计算资源预测系统架构图如图3所示,图中VM为虚拟机.该系统结构图从宏观的角度给出了一个基于三支决策的云资源预测系统所需要具备的功能及大致流程.
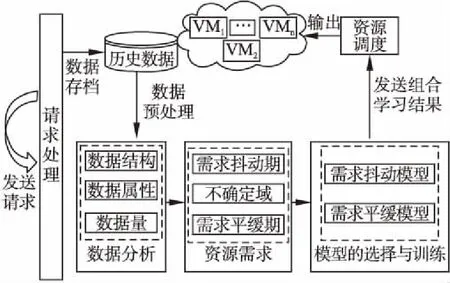
图3 云计算资源预测系统架构图
对云平台的历史数据中的用户请求进行分析,包括数据结构,数据属性和数据量等,在系统数据预处理模块中,直接筛除无关数据及属性,并将有用的原始数据进行规范化.
为了实现精准有效的预测,根据数据特征进行模型的选择和训练,我们引入相邻值之间的均方根误差(Root Mean Squared Error,RMSE),设定阈(α,β)值进行对比,对平稳期、波动期和抖动期的三种情况进行分析,给出区分不同情况的三支方法准则.对于用户资源需求划分的三个区域,我们仅采用两种预测模型来进行预测,对于负载平缓期往往采用适用于平稳的,具有线性趋势的时间序列预测模型,而对于负载抖动期本文采用短期预测模型来更好的拟合.而对于中间不确定域即负载波动期,本文给出一个评价标准,采用代价评估的三支决策边界域处理模型来进行再划分.使用最终预测结果来规划容量.
3.2 基于代价评估的三支划分
基于三支决策的云资源负载预测模型,构建状态空间Ω={X,XC}分别表示在云资源环境中的负载特征,X表示负载平缓期预测模型,XC表示负载抖动期预测模型,样本经过训练后划分到三个域,正域(POS)、边界域(BND)和负域(NEG).给出决策方案为D={aP,aB,aN},分别表示判定负载状态后的三种决策方案,平缓期立即处理,波动期延迟决策再处理,抖动期立即处理.鉴于此,针对不同状态下的决策动作,设立如下决策代价表,如表1所示.
表1中λij(i=P,B,N,j=P,N)表示对象属于X和XC状态下采取的不同行动aP、aB、aN的损失值,即代价.P(X|[x])表示等价类中一个对象属于集合X的条件概率.对于一个对象,采取不同的决策动作时,会带来不同的代价,因此,不同的决策动作带来的期望损失如下:
R(aP|[x])=λPPP(X|[x])+λPNP(XC|[x])R(aB|[x])=λBPP(X|[x])+λBNP(XC|[x])R(aN|[x])=λNPP(X|[x])+λNNP(XC|[x])
(11)
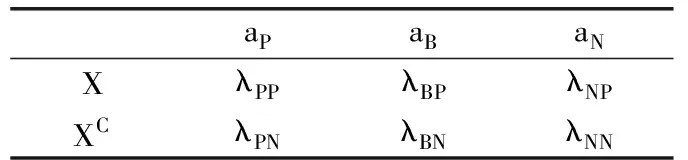
表1 负载预测代价函数
依据贝叶斯最小风险准则,最佳方案为期望损失最小的决策方案,有如下规则:
(P)如果R(aP|[x])≤R(aB|[x])且R(aP|[x])≤R(aN|[x])成立,则判定x∈POS(X)(平缓期预测模型);
(B)如果R(aB|[x])≤R(aP|[x])且R(aB|[x])≤R(aN|[x])成立,则判定x∈BND(X)(波动期延迟决策);
(N)如果R(aN|[x])≤R(aP|[x])且R(aN|[x])≤R(aB|[x])成立,则判定x∈NEG(X)(抖动期预测模型);
考虑到对于含有两种状态的决策系统,记P(X|[x])=P,则P(XC|[x])=1-P,上述规则只与概率P(X|[x])和相关的总代价有关.考虑到在[x]⊆X时,将x判定为平缓期的代价要小于将其判定为波动期的代价,进一步小于将其判定为抖动期的代价.在[x]⊆XC时,将x判定为抖动期的代价要小于将其判定为波动期的代价,进一步小于将其判定为抖动期的代价.可以得到λPP≤λBP<λNP,λNN≤λBN<λPN.
依据三支决策模型的决策准则,规则(P)、(B)和(N)可简化为:
(P1)当P(X|[x])≥α时,x∈POS(X),则采用平缓期预测模型;
(B1)当β (N1)当β≥P(X|[x])时,x∈NEG(X),则采用抖动期预测模型; 其中α和β分别为: (12) (13) 算法1.基于代价评估的边界域处理模型算法 输入: Ti:中间域样本数据BND(X)={x1,x2,…,xs} 输出: 平缓期POS(X)和抖动期NEG(X) Step 1. 从BND(X)中任取一样本xb,根据公式(13)计算出样本被划分到平缓期和抖动期的损失Cost(aP|[xb])和Cost(aN|[xb]) Step 2. xb∈NEG(X) else xb∈POS(X) Step 3. if(xb∈POS(X))then POS(X)=POS(X)∪xb BND(X)=BND(X)-xb if(xb∈NEG(X))then NEG(X)=NEG(X)∪xb BND(X)=BND(X)-xb. Step 4. 若边界域中所有样本都被成功划分到平缓期和抖动期,即边界域为空,则结束.否则,转Step 1,知道所有边界域样本被划分成功. 借助三支决策的基本思想,分析Google trace中真实云负载数据,将对象划分为正域(POS)、边界域(BND)和负域(NEG),提出了一种基于三支决策的云资源需求预测模型(DMASVR-3WD),其系统架构,如图4所示. 图4 三支预测模型系统架构 对于平缓期和抖动期,直接借助2.2节和2.3节提到的两种基本预测模型进行负载预测处理,基于平缓期的特点,本文采用二次移动平均法(DMA)进行资源负载的预测.基于抖动期的特点,本文采用支持向量回归模型(SVR)进行资源负载的预测.如果将固定因素影响的样本点看作是平缓期,那么受到随机因素影响的即偏离原始样本集的样本点,偏离原始样本集趋越大说明负载的变化越明显,即表现为负载的抖动期.本文针对抖动期和平缓期的负载特点,使用均方根误差(RMSE)来划分负载平缓期,抖动期和波动期,由此本文提出了DMASVR-3WD算法. DMASVR-3WD预测模型提出的目的是为了实现更加精准的云资源负载预测,提高资源利用率以降低成本.我们引入均方根误差RMSE标准来计算代价.负载预测代价计算方法为: (14) 当对真实的云资源负载数据进行预测分析时,根据负载特征划分三部分,其预测准确率也同样包括三部分,其中R1、R2和R3分别表示负载特征平缓时平缓期预测模型,波动期延迟决策和抖动期预测模型的代价. (15) (16) (17) (18) 基于上述讨论,我们给出DMASVR-3WD模型的具体算法如下: 算法2.DMASVR-3WD预测模型 输入: Ti:历史cup请求量数据集时间序列 X={xi,xi-1,…,xi-(w-1)} 输出: P:cup请求量的预测值 //计算相邻值之间的均方根误差 fori=w;i //m为时间序列的长度 //w为DMA窗口的大小 Mi+1=DoubleMA(w,xi,xi-1,…,xi-w+1) //DMA根据最近w个输入值预测线性分量Mi+1 fori=w+1;i Ri=Ti-Mi //Ri为时间序列的非线性分量 fori=w+1;i (C,K,s)=SVRtrain(Ri,Ri+1) //Ri表示输入数据,Ri+1表示输出数据,训练SVR模型 //C表示惩罚系数,K表示核函数,s表示损失函数参数 Nm+1=SVRpredict(c,g,p,Nm) P=Mm+1; P=Rm+1; else P=Rm+1 else P=Mm+1 本文实验操作系统为64位CentOS 7,内存为8GB,硬盘容量为50GB.在此操作系统上利用Java,在IDEA开发平台上进行评估实验. 图5 数据预处理示意图 实验数据来自于Google cluster trace,其中的数据表task_usage记录了近29天各个时间节点的主机CPU,内存,磁盘等资源使用信息,本文的目的是预测CPU的使用情况,因此选取了表中某几天的CPU使用状态信息,以30分钟为单位,对表中CPU使用量进行统计,并将其定义为一个批量数据集(Batch),基于此,再把每3个连续的Batch划分为一个滑动窗口(Window),其移动间隔为一个Batch的长度,如图5所示. 为了评价预测系统的性能,实验采用合格率,准确率与SLA违约率三个评价指标.对于所选取的指标含义及选取依据解释如下: 1)合格率(QR) 由于在实际集群环境中进行资源分配,很难达到资源需求和资源供应完全一致,为了提高用户服务质量,获取更多的分配资源,本文引入合格率作为其中评价指标,用来表示负载预测值大于实际值的样本比例. (19) 2)准确率 若提供商仅仅为保证较高的服务质量,保持较高的合格率,将会导致预测值常常大于实际值的情况,即存在资源分配过度,使用率低和能耗较高的问题.由此为避免大量资源闲置的情况出现,本文引入检验动态资源需求预测偏差的指标,预测值与实际值的均方误差(RMSE)指标和平均绝对百分比误差(MAPE): (20) (21) 3)SLA违约率(SLA) 在实际的集群环境中,云计算平台资源需求存在高度动态性,处于抖动期的负载,资源需求短时间内增长幅度大,容易出现实际值大于预测值的情况,导致作业资源短缺,服务质量下降的问题,由此本文引入了SLA违约率指标,其表示为预测值小于实际值的样本点所占比例: (22) 实验截取了Google cluster trace某几天的数据,并进行上述的预处理工作,得到多个聚合的windows数据集,再将windows中的多个batch数据作为模型输入,得出预测值与实际值的对比结果,本节分别评估了自移动积分滑动平均(ARIMA)、神经网络(NN)和DMASVR-3WD算法三种预测模型对于实际CPU使用的预测效果,评估指标分别为合格率,均方误差,平均绝对百分比误差与SLA违约率.三种预测模型的预测结果对比如图6所示. 4.3.1 自回归积分滑动平均(ARIMA) 从图6中可以观察到,ARIMA对平缓期的CPU使用量具有较好的预测效果,但在CPU资源使用的抖动期间,ARIMA模型的预测效果并不稳定,有明显的滞后性,8-22区间中滞后性明显.且多处预测值低于实际值,特别是在9~12区间和13~15区间中,明显观察到预测值低于实际值.滞后性明显使得无法准确了解CPU的资源使用情况,容易导致资源短缺,进而影响集群的服务质量. 4.3.2 神经网络(NN) 从图6的观察中得到,NN对平缓期的CPU使用有着更为理想的预测效果,但算法本身容易陷入局部最优解,因此对抖动期的CPU使用的预测略显不足,难以适应突增的资源使用变化,如8~20区间的预测曲线平缓,与实际值的预测差距较大,CPU资源使用的预测不足,致使其既不能保证很高的服务质量,也存在资源短缺现象发生. 图6 三种模型预测结果对比图 4.3.3 DMASVR-3WD算法 基于同样的数据集,本文提出的DMASVR-3WD模型相较于ARIMA与NN算法,DMASVR-3WD算法在CPU使用的平缓期与抖动期的表现都较为稳定,特别是对抖动期的预测,如12~17区间的预测效果,能较好地拟合实际CPU使用的曲线,且多数节点的预测仅仅稍大于实际的CPU使用量,如17-21区间的预测效果,这样可在保证较高的服务质量的同时,也能减少资源闲置的现象发生. 基于上述实验,计算得出的有关ARIMA,NN与DMASVR-3WD预测模型的评价指标结果,如表2所示. 表2 模型预测评价指标对比 Table 2 Model prediction evaluation index comparison QRMSEMAPESLAARIMA0.6000.0331.1340.400NN0.5000.0491.0970.500DMASVR-3WD0.6670.0140.3930.333 从表2中可以看出,NN算法有较小的合格率和较大的违约率,即在时间节点上多数的预测值小于真实值,并且有着较大的均方误差和平均绝对百分比误差,即预测准确度低,这些将使得用户作业无法获取资源进而处于等待状态,延长了作业时间,进而影响了集群的使用效率.相较于NN算法,ARIMA算法有着更好的合格率和违约率,但是由于其无法适应突增负载状况,使得该模型有着较高的均方误差和极大的平均绝对百分比误差.同时,我们观察DMASVR-3WD算法,有理想的QR和更少的违约率,同时预测结果MAPE的标准差仅为0.393,远低于其他预测算法,体现了该算法具有良好的稳定性.也因为该算法能很好的拟合负载抖动期和平缓期的真实CPU使用量,因此,有着低的MSE,相比较于其他两种算法,DMASVR-3WD模型明显提高了预测精度. 为了检验DMASVR-3WD的泛化能力,从Google cluster trace的task_usage即任务资源使用表中选取三张负载数据表采样数据进行对比预测,预测结果如图7所示,评价指标对比结果如表3所示. 图7 不同数据集的预测结果 表3 不同数据集模型预测评价指标对比 从表3和图7可知,DWASVR-3WD在不同时期的云计算资源负载预测中均能取得较高的精度和较低的违约率,虽然在task_usage_494的CPU资源请求量波动较大,但是仍然取得了较高的预测精度,这充分表明了该预测方法具有较好的稳定性和泛化能力. 为了提高云计算资源负载预测的准确度,保证服务质量,提出了一种基于三支决策的云平台负载预测模型(DMASVR-3WD).在分析了用户资源需求的负载特征后,引入基本预测模型对平缓期和抖动期进行处理,分析并且计算出代价阈值,依据期望损失代价最小化的原则对波动期进行划分处理.使用合格率,RMSE,MAPE和违约率四种评价指标,评估本文提出的负载预测模型和现有的负载预测模型在真实Google cluster trace数据中的预测效果.实验表明,DMASVR-3WD算法能够有效地降低预测误差,同时在平缓期和抖动期都起到很好的预测效果,并且有着较低的违约率.3.3 代价评估的三支决策边界域处理模型
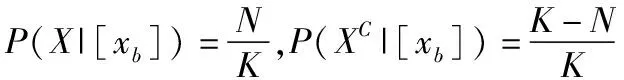
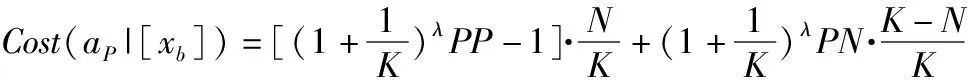
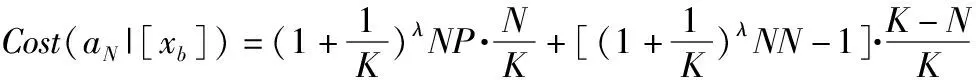
3.4 DMASVR-3WD预测模型

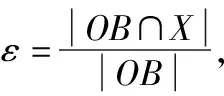
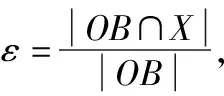
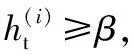
4 实验结果与分析
4.1 实验环境及数据集
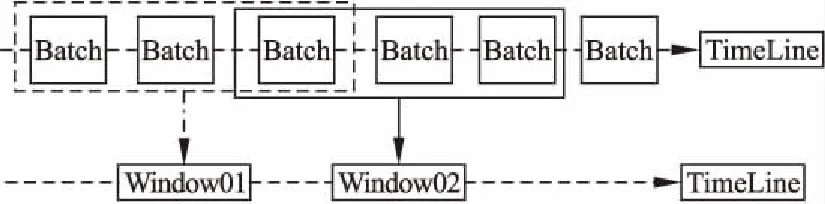
4.2 评价指标
4.3 预测效果对比与分析
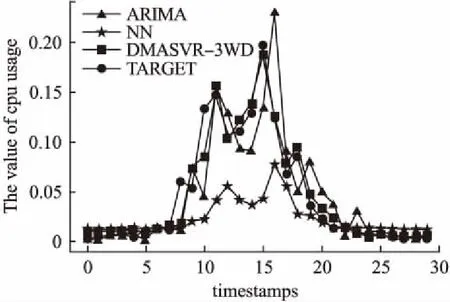
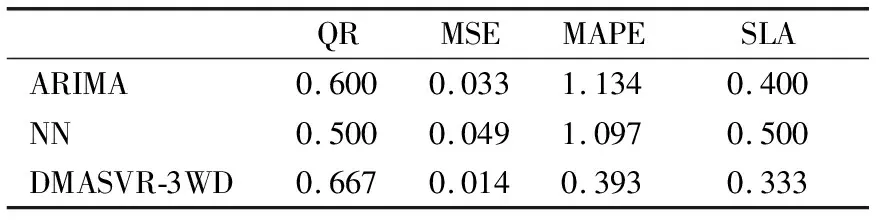
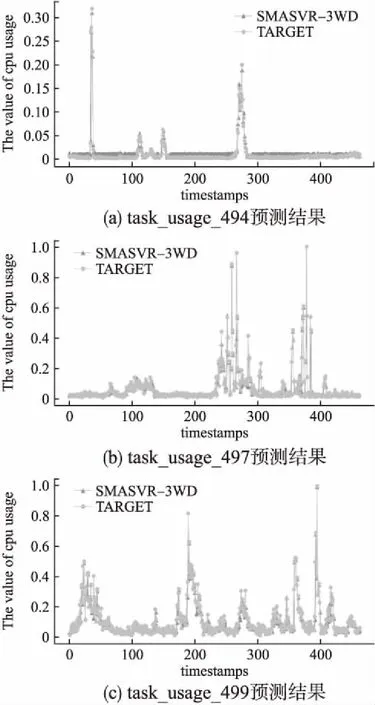
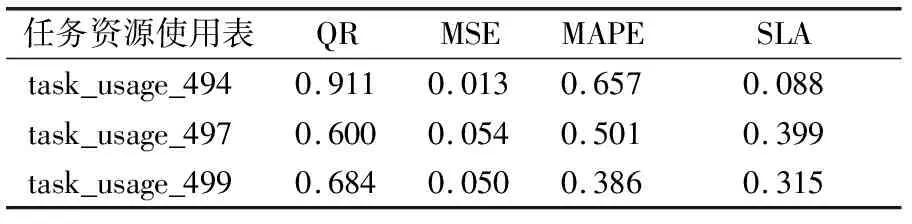
5 结 论
