直线与椭圆位置关系的判定定理别证与推广
2020-07-03湖南省隆回县第二中学422200彭利波
中学数学研究(江西) 2020年6期
湖南省隆回县第二中学 (422200) 彭利波
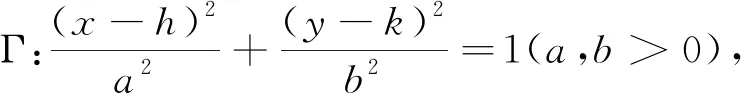
(1)当d=1时,直线l与椭圆Γ相切;
(2)当0≤d<1时,直线l与椭圆Γ相交;
(3)当d>1时,直线l与椭圆Γ相离.
文[1]所利用到的平移变换、伸缩变换都是仿射变换的一种特殊形式,在高中教材中作为选修内容出现,在高考中直接份量不多,故在平时教学中要求较低.相对而言,作为选修内容出现的椭圆的参数方程这一内容会比较熟悉,本文将利用文[2]中椭圆的参数方程解法对这个定理给出一个通俗易懂的证明.
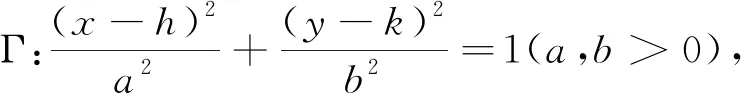
(1)由sin(θ+φ)=±1在θ∈[0,2π)上有唯一解,此时直线l与椭圆Γ有一个交点.即d=1时,直线l与椭圆Γ相切;
(2)由-1 (3)由sin(θ+φ)>1在θ∈[0,2π)上无解,此时直线l与椭圆Γ没有交点.即d>1时,直线l与椭圆Γ相离(证毕). 类似的,利用该法可以推导出直线与双曲线位置判定定理.证明过程留给读者,结论如下: (1)当d=1时,直线l与双曲线Γ相切; (2)当0 (3)当d>1时,直线l与双曲线Γ相交; (4)当d=0时,直线l与双曲线Γ相交或相离(相离时直线为双曲线的一条渐近线).
