构建函数关系巧求两道几何最值问题

浙江金华第一中学 (321015) 吴贤盛

本文拟通过归类举例的形式，着重说明：结合图形，适当构建函数关系，有利于迅速探求有关求解体积、周长、面积的最大值问题，进而逐步提高分析、解决问题的实际能力.

图1

例1 (2017年全国Ⅰ卷·理16)如图1，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为.

分析：本题首先要结合题意画出三棱锥，并明确该三棱锥的特性；其次，需要结合图形，灵活设元(即设出有关线段的长度)，并构建三棱锥体积的函数表达式，以便借助导数巧求最大值.

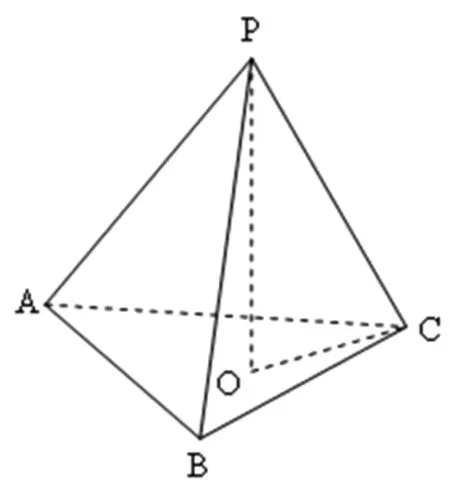
图2

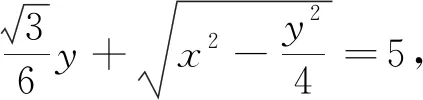
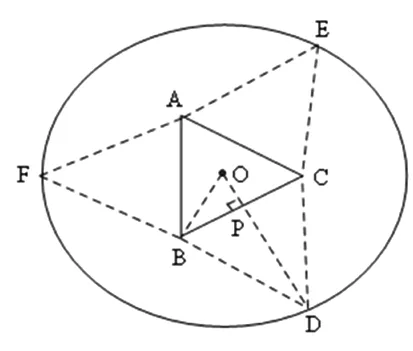
图3

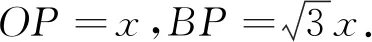
评注：本题涉及立体几何中熟悉的折叠问题，难点在于如何得到三棱锥体积的函数表达式.方法一实际上就是构建了三棱锥的体积关于等边ΔABC的边长的函数表达式，显得较为繁琐；方法二实际上就是构建了三棱锥的体积关于线段OP长度的函数表达式，显得较为简捷，同时也凸显了该题设计的精妙之处——以熟悉的图形折叠为载体，以熟悉的特殊的直角三角形(RtΔOBP)为解题切入点，以熟悉的正三棱锥的体积公式为纽带，突出体现了函数的应用以及导数的应用.故该题对考生独立分析问题、解决问题的实际能力提出了较高的要求，对考生的基本数学素养和内在潜能的考查比较深刻、到位，有利于增强考生运用数学的意识，学会将实际问题抽象为具体的数学问题，进一步感受数学的应用价值，值得品味.

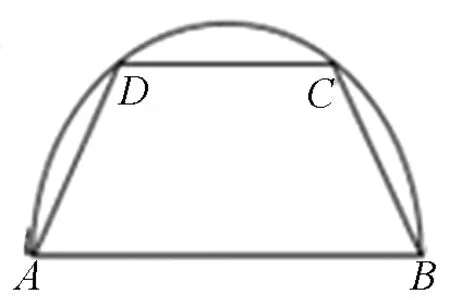
图4

例2 (新课标人教A版第112页复习参考题A组第7题改编)如图4，将一半径为2的半圆形纸板裁剪成等腰梯形ABCD的形状，下底AB是半圆的直径，上底CD的端点在圆周上，则所得梯形周长的最大值为.

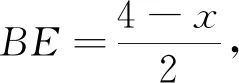
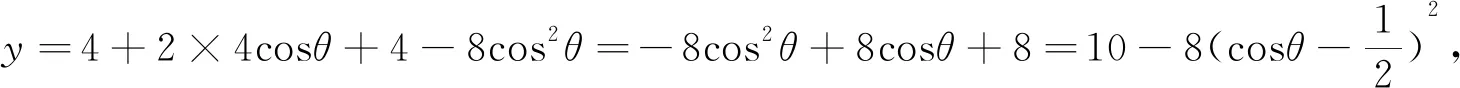
(法4)设AB的中点为O，连接CO,AC，过点C作CE⊥AB于E，则由AB是半圆的直径得∠ACB=900，从而由射影定理得BC2=BE·AB.

评注：上述方法1、方法2都是以设边长为切入点，对比可知方法1简单一些(转化为二次函数“配方”求最值)，方法2相对繁琐(借助复合函数“求导”求最值)；方法3、方法4都是以引入辅助角(即设角)为切入点，对比可知方法3简单一些(灵活运用“配方法”求最值)，方法4相对繁琐(借助复合函数“求导”及三角函数知识求最值).

综上，求解与图形有关的最值问题，若能适当构建函数关系，并借助导数知识加以灵活处理，则往往可顺利获解；同时也较好地培养了数学抽象、直观想象、数学运算的核心素养.