贝叶斯响应变量适应性随机化模拟预测评价方法初探*

东南大学公共卫生学院流行病与卫生统计学系(210009) 范 扬 李太顺 杨嘉莹 王诗远 刘 沛

【提 要】 目的 探索贝叶斯响应变量适应性随机化的模拟预测评价方法，为研究者在临床试验中合理设计随机化方案提供借鉴。方法 通过不同参数组合成不同场景，使用R语言编程实现试验模拟过程，构造评价指标，结合模拟试验结果对不同场景作出评价。结果 在结局指标为二分类高优变量的两臂临床试验中，可以通过调整分配概率更新频率、固定随机化阶段长度、分配概率算法调节参数及各处理组的先验概率分布，获得理想的检验功效及伦理性。在试验前可以通过提高试验成功界值、降低分配概率更新频率、增加均衡分配期长度三种方法降低试验整体一类错误率，以满足监管部门的要求。结论 本研究提出的贝叶斯响应变量适应性随机化模拟预测评价方法可通过设定场景参数模拟试验，从控制一类错误、保证检验效能、提升伦理性等方面较全面评价随机化方案的合理性。

适应性随机分组方法一直是临床试验领域近二十年来研究的热点问题之一[1-3]。相较于传统分组概率固定不变的随机化设计，适应性随机更加灵活。通过不断调整后续分配概率，使更多受试者被分入当前疗效更好的组中。目前关于适应性随机化的研究成果较为丰富：Wei等[4]提出了随机化的胜者优先原则(randomized play-the-winner rule,RPW)；Ivanova[5]介绍了劣者淘汰原则；Thall等[6]介绍了基于贝叶斯思想的随机分配概率调整方法。国内于莉莉等[7]对瓮模型及RPW原则进行了研究；刘晓燕等[8]对响应变量适应性随机化进行了研究；陈冬等[9]对贝叶斯适应性随机化进行了介绍。其中，贝叶斯响应变量适应性随机化(Bayesian response-adaptive randomization,BRAR)，因能利用先验信息的点估计值及方差，相比使用频率学方法的适应性随机化仅利用点估计值[10]，对随机分配概率的调整更加合理而受到青睐。然而我们接受任何一种新的统计方法时，必须了解其可能存在的两面性：响应变量适应性随机化方法所具有的伦理优势，往往通过牺牲其随机性与检验效能得到；在试验入组时不断调整分配概率，会明显增加操作上的难度；在引入贝叶斯有信息先验时，常常会引起一类错误的膨胀等。因此对BRAR方法进行正确评价具有实际意义，而目前国内尚未见到相关报道。本文旨在探索BRAR评价方法的基础上，研究其模拟预测评价模式和统计特征，以期为正确理解BRAR方法及制定BRAR方案提供参考。

原理与方法

1.BRAR原理及操作流程

本研究以结局指标为二分类高优变量的两臂临床试验为例阐述BRAR原理及操作流程。设各处理组x反应率θx的先验为Beta分布，即θx～Beta(ax,bx);x={1,2}。将整个BRAR过程分为开始阶段的固定随机化和后续的动态随机化两阶段：在固定随机化阶段采用等概率随机化方法，即每例受试者固定有50%的概率被分配至试验组或对照组，而在动态随机化阶段该入组概率随数据积累被不断调整。固定随机化阶段受试者入组完毕后采集数据，记nx个受试者中出现阳性结果的个数为sx，似然函数为二项分布，即sx～Binomial(nx,θx);x={1,2}。由贝叶斯定理更新各组反应率θx，可得后验分布θx|Sample Data～Beta(ax+sx,bx+nx-sx);x={1,2}。之后进入动态随机化阶段：

(1)求解不等式 按Cook[11]提出的方法求解随机变量概率不等式Pr(θ1>θ2)、Pr(θ2>θ1)：

(1)

上式中fθ1(x)为服从Beta分布的随机变量θ1的概率密度函数，Fθ2(x)为服从Beta分布的随机变量θ2的累积分布函数；

(2)判断是否停止试验 根据如下规则：尚未达到最大样本量时，若Pr(θ1>θ2)大于早期成功界值，因早期成功而停止试验；尚未达到最大样本量时，若Pr(θ1>θ2)小于早期失败界值，因早期失败而停止试验；达到最大样本量时停止试验，若Pr(θ1>θ2)大于最终成功界值，记为试验成功；在任何时候，若Pr(θx>θmin)小于无效界值，其中θmin为无效阈值，因判定该组处理无效而停止试验；

(3)更新分配概率 计算受试者被分配至组1、组2的概率Prto1、Prto2：

(2)

上式中TP为调节参数(tuning parameter)，有TP∈[0,1]以修饰分配概率变化的程度；

(4)产生分配结果 使用非等概率分配方法，结合(3)中Prto1和Prto2，产生下一例受试者SUBi的分配结果；

(5)更新未知参数分布 采集SUBi数据，使用贝叶斯定理更新反应率θx的概率分布，返回步骤(1)并递增i，直到在步骤(2)中停止试验。

2.模拟预测评价

适应性设计的模拟预测评价指在试验开始前，将适应性设计中各参数的取值组合视为一个场景(scenario)，使用计算机载入该场景然后产生模拟数据，通过比较各评价指标在不同场景下的模拟结果进行预测评价。适应性设计的模拟预测评价能够指导研究者改进试验方案，将这种技术运用于BRAR方案设计，即可达到在提高试验伦理性的同时控制一类错误及检验功效的目的。BRAR模拟预测评价的要素包括场景参数、评价指标及模拟方法实现，本研究使用R语言依据上文所述原理及操作流程编写模拟试验程序。

(1)场景参数

场景参数可分为试验相关参数和模拟循环相关参数两类。试验相关参数包括最大样本量、分配概率更新频率、固定随机化阶段长度、试验停止界值、各处理组反应率、处理组数量、分配概率算法调节参数TP、各处理组先验概率分布；其中试验停止界值再细分为早期成功界值、早期失败界值、最终成功界值、无效界值四种。若根据式(1)计算出的组1反应率分布大于组2反应率分布的概率值Pr(θ1>θ2)超过一定阈值(一般取0.975)，则可认为此时组1疗效相比组2足够优秀而提前停止试验，定义该阈值为早期成功界值；同理，若Pr(θ1>θ2)<0.025，则称阈值0.025为早期失败界值，在两臂试验中早期成功界值与早期失败界值和为1。当试验因达到最大样本量停止时，若此时Pr(θ1>θ2)>0.900，则称试验停止时有足够理由证明组1疗效更好，定义阈值0.900为最终成功界值。模拟循环相关参数一般有循环次数及一些试验结果记录变量。上述任一场景参数的取值变化都会导致随机化效果的相应变化。

(2)评价指标

BRAR的评价指标可根据试验终止原因、终止试验时各组受试者人数、成功数、失败数等模拟试验的结果来构造。包括：

①一类错误率α′：此处的α′为通过模拟获得的一类错误率。其含义与频率统计事先定义的一类错误率α相同：即当场景参数中各处理组的反应率被设为相同值θ1=θ2时，进行N次模拟，其中有n1次模拟得出组1和组2反应率不同的概率，即α′=n1/N。

②检验效能1-β′：此处的1-β′为通过模拟获得的检验效能。其含义与频率统计事先定义的检验效能1-β相同：即当场景参数中各处理组的反应率被设为不同值θ1≠θ2时，进行N次模拟，其中有n2次模拟正确得出组1和组2反应率不同关系的概率，即1-β′=n2/N。

③平均样本量：因试验具有早期停止规则，所以每次模拟试验并不会都达到最大样本量。在确定了场景参数和两组的反应率后，进行N次模拟试验可得N个试验终止时的总受试者人数：其均数μSS可评价该场景对样本量的需求；标准差σSS可评价稳定程度。

④优劣分配比R：当场景参数中各处理组反应率被设为不同值θ1≠θ2时，记试验终止时真实较优组中受试者数量为nS、较劣组为nI，则优劣分配比r=nS/nI。进行N次模拟试验可得N个R值：其均数μR可评价该场景的伦理性；标准差σR可评价稳定程度。

⑤总失败数TF：记试验终止时试验组、对照组的失败数分别为m1、m2，则总失败数TF=m1+m2。进行N次模拟试验可得N个TF值：其均数μTF可评价该场景的伦理性；标准差σTF可评价稳定程度。

实例与结果

因目前国内未见贝叶斯响应变量适应性随机化的应用实例，我们借鉴Tamura等[12]报告的使用盐酸氟西汀治疗抑郁症门诊病人的临床试验，运用本研究提出的模拟试验技术评价BRAR表现。

盐酸氟西汀试验采用双盲、安慰剂对照的RPW(1,1)适应性设计，将89例门诊病人按快速眼动期(rapid eye movement latency,REML)长短分为短REML层共45例、正常REML层共44例；以“经3周治疗后，相邻两次HAMD17评分下降50%认为成功”作为无延迟替代指标；先将每层前6例受试者按随机区组分配，再按RPW原则入组后续受试者；试验结束时，短REML层脱落4例、试验组共21例、对照组共20例，正常REML层脱落2例、试验组共21例、对照组共21例。

1.场景参数设定与模拟结果

本研究在原方案短REML层基础上结合BRAR要求，设置相关参数。因盐酸氟西汀试验方案中预计短REML层招纳50例受试者，设置场景参数中最大样本量为50；取固定循环次数为10000、随机种子数为20190622、早期成功界值为0.975、早期失败界值为0.025、最终成功界值为0.900。不同场景及参数设置如表1所示。每个场景中分别为组2设置两个反应率θx：满足θ1=θ2时可计算一类错误率α′；满足θ1≠θ2时可计算检验效能1-β′。场景1参照盐酸氟西汀试验，设分配概率更新频率为1、固定随机化阶段长度为6、算法调节参数为1、两组均取无信息先验Beta(1,1)，并以此作为标准参照BRAR方案，与盐酸氟西汀试验的RPW(1,1)设计及其他场景进行比较。场景2～6在场景1的基础上，依次改变分配概率更新频率、固定随机化阶段长度、分配概率算法调节参数及各处理组先验概率分布。根据盐酸氟西汀试验“对短REML层，预计安慰剂组反应率为0.2，试验组反应率为0.5”，即“组1均数0.2，标准差0.15；组2均数0.5，标准差0.19”，可构造有信息先验Beta(1.22,4.89)和Beta(3.37,1.45)。

模拟试验结果如表2。可见不同场景下各评价指标均有变化，故各场景模拟结果可为BRAR方案设计提供参考。当组2反应率θ2=0.2时，两组反应率相同，关注一类错误率，并可取不同场景的值进行纵向比较；同理，当组2反应率θ2=0.5时，两组反应率不同，关注检验效能，并可取不同场景的值进行纵向比较。纵向比较分析详见文章讨论部分。

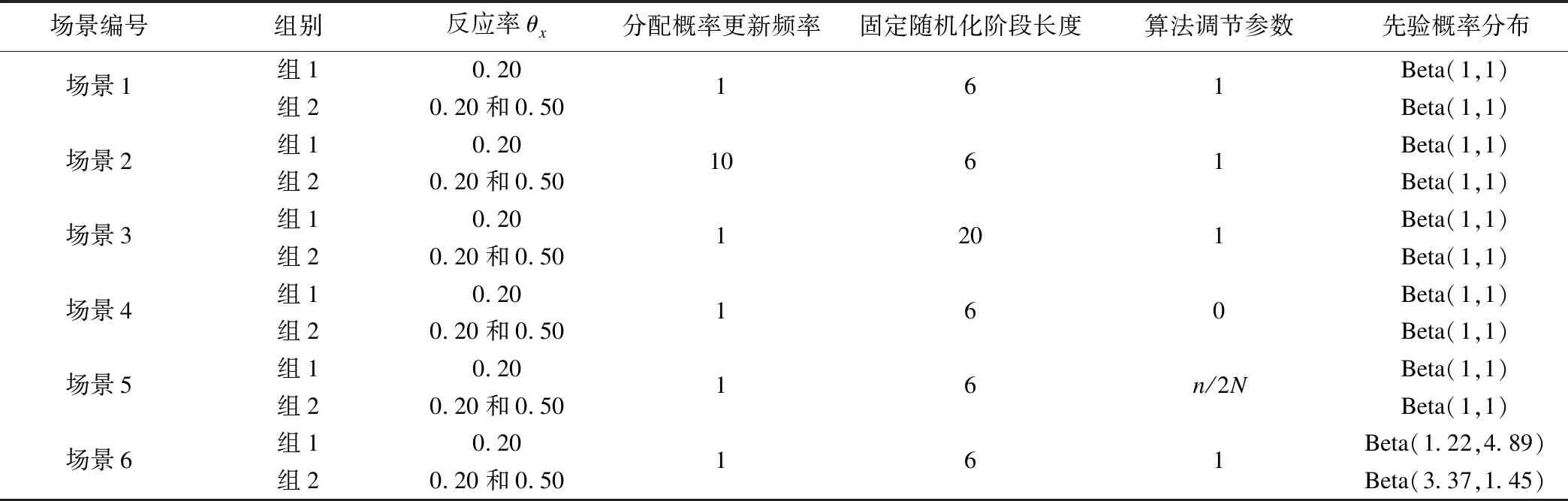
表1 盐酸氟西汀试验BRAR模拟场景及参数设置

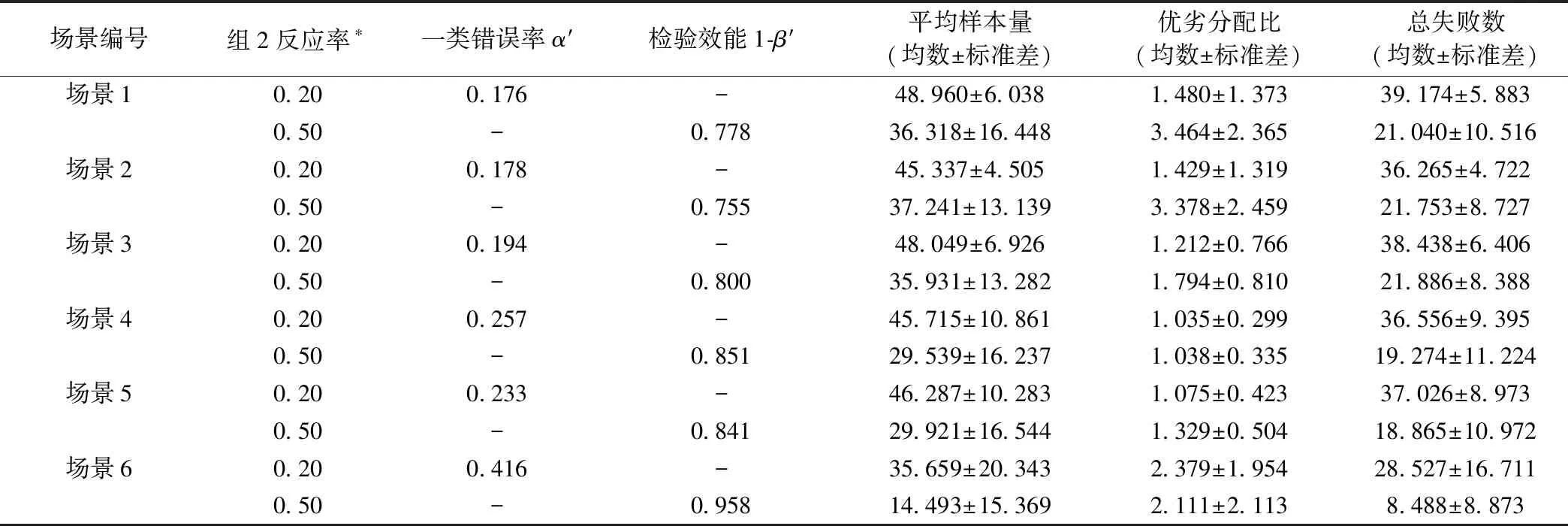
表2 不同场景的模拟试验结果

*：组1反应率均设为0.2。

2.一类错误率控制

通过提高试验成功界值、降低分配概率更新频率、增加固定随机化阶段长度三种途径，可以降低整体一类错误率。表2结果提示，在盐酸氟西汀试验背景下，降低分配概率更新频率、增加固定随机化阶段长度对控制整体一类错误率效果并不明显，因此本研究尝试通过提升试验成功界值，使得整体一类错误率小于0.10或0.05。探索过程如下：从常用的早期成功界值取0.975、早期失败界值取0.025、最终成功界值取0.900开始，首先固定最终成功界值，提高早期成功界值，计算整体一类错误率；如果不能满足要求，此时开始提高最终成功界值，直到整体一类错误率降低至合适水平。表3所示为在场景1的基础上，依据上述探索过程控制整体一类错误率的模拟试验结果。

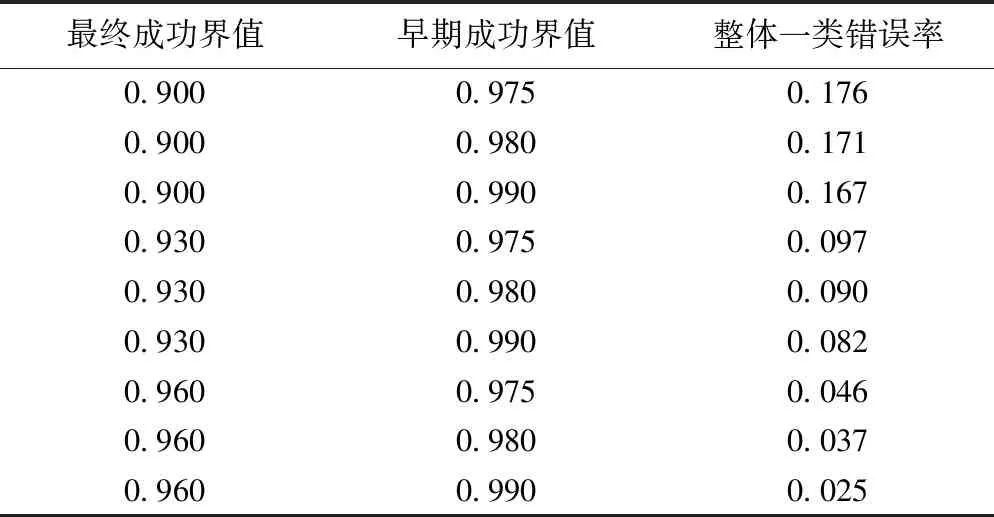
表3 在场景1条件下提升试验终止界值控制一类错误率

针对表1六种不同场景，采取上述方法控制整体一类错误率小于0.10，计算结果如表4所示。当BRAR方案参照场景1设计时，如果取早期成功界值为0.975、早期失败界值为0.025、最终成功界值为0.930，则最终能将整体一类错误率控制在0.097。

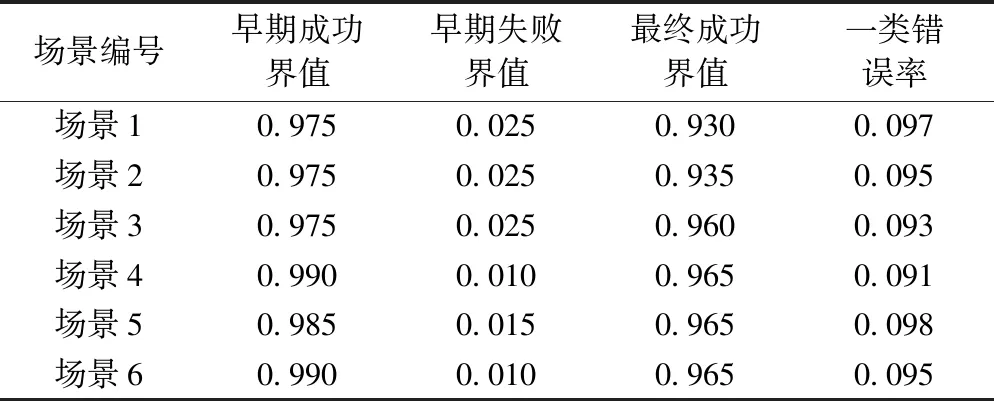
表4 提升试验终止界值控制六种场景一类错误率

讨 论

BRAR相比固定随机化是一种新颖且更注重伦理性的分配方法，只要在实际试验前借助计算机技术通过细致的模拟试验探讨评价多种可能性，制定合理的随机化方案，就能最大程度发挥其优势。对本次研究，比较场景1和场景2，提高分配概率更新频率能够稍微提高检验效能，也能稍微提高优劣分配比，使稍多的受试者被分配至疗效较好的组中。对比场景1和场景3，增加固定随机化阶段长度能够提升检验效能，但是会降低优劣分配比、升高一类错误率，原因是其相当于缩短BRAR过程，导致整个随机化更偏向固定随机化。对于式(2)中调节参数TP取值，有多个研究给出了不同尝试：Rosenberger等[13]、Connor等[14]在其研究中取TP=0.5。本研究场景1中令TP=1，由式(2)可知此时受试者被分配至每组的概率分别为Pr(θ1>θ2)、Pr(θ2>θ1)，相比TP取其他值的场景4和场景5，优劣分配比的标准差明显较大。观察场景4，若令调节参数TP=0，根据式(2)可得Prto1=Prto2=0.5，且分配概率始终保持不变，则整个随机化流程相当于具有提前终止规则的、使用贝叶斯方法的固定随机化，因此会平均两组受试者数量、使优劣分配比接近1，导致检验效能显著提升，同时一类错误率升高。Thall等[6]提出可取TP=n/(2N)，其中n为当前样本量、N为试验最大样本量，则试验开始时有TP=0、最后一例受试者入组时有TP=0.5，过程中TP∈(0,0.5)；Bello等[15]将其推广至三臂试验；观察场景5，确实TP=n/2N可以缩小优劣分配比及其标准差，表示该方法对分配概率的调整更加保守。对比场景1和场景6，当使用的先验信息能够正确表达两组的实际反应率θx的差别时，BRAR能够大大降低样本量及总失败数，善用历史信息是使用贝叶斯响应变量适应性随机化相比频率方法所具备的巨大优势；至于本试验观察到的“使用有信息先验时得到的优劣分配比反而较低”，一个可能原因在于此时样本量相比使用无信息先验较小(仅14.493例)，故优劣分配比有所降低；需要注意的是，引入有信息先验虽然会明显提升检验效能，但是需要付出一类错误膨胀的代价。盐酸氟西汀试验短REML层实际招募了45例受试者，使用RPW(1,1)原则将24例分入试验组、21例分入对照组，优劣分配比为1.143、总失败数为23；使用BRAR，在场景1中平均需要招募36例受试者，优劣分配比为3.5、总失败数为21。不难看出，BRAR相比RPW(1,1)，将受试者向疗效更佳的处理组中分配的能力更强，因此对伦理性提升更加明显，同时可减少总失败数及样本量。

综合分析本试验结果，BRAR确实能够提升试验伦理性，将更多受试者分配至疗效更好的处理组中，但其代价是降低了检验功效。不可否认，功效的下降确实是所有适应性随机化方法相比传统固定概率随机化方法的短板：从宏观上看，固定随机化能够高效迅速地区分不同处理组的疗效，使该试验外的广大群众能够快速地从结果中获益。然而站在另一个角度思考，不仅参加该试验的受试者其本身希望得到更加妥善的治疗，将他们分配到当前更优的处理组也是伦理上必须考虑的。尤其是研究罕见病或者需要纳入很多受试者的临床试验，我们更愿意且需要将目光聚焦于当下，将精力集中于提升个体伦理而非群体伦理，因此检验功效的降低变得可以被接受，对BRAR的使用也达到了“投其所长，避其所短”。使用本研究提出的模拟预测评价方法合理设计BRAR方案，也可以提高检验功效：如提高分配概率更新频率、增加固定随机化阶段长度、增大分配概率算法调节参数可稍许提高检验功效；而结合有信息先验可显著提高BRAR的检验功效，但需注意控制一类错误的膨胀。

BRAR既然使用了贝叶斯方法，那么先验分布的选择必然是无法逃避的话题。使用多个不同先验是贝叶斯分析中常采取的方法，本研究在模拟评价中尝试使用了有信息乐观先验和无信息先验，后续研究可以进一步增加先验数量。本研究建议在设计BRAR方案时尽量选择多个先验以获得更加全面认识，而在实际试验使用BRAR分配受试者时使用无信息先验，防止由于选择了不恰当先验导致试验效果不尽人意。有研究[16-17]指出“相比于两臂临床试验，BRAR更适合在两臂以上的临床试验中应用”，本研究仅关注了结局指标为二分类变量的两臂临床试验，也确实发现在这种情景下BRAR对固定随机化并无压倒性优势，而且其对检验效能的降低也不能忽视。因此本研究建议后续在三臂至多臂试验的情景下，尝试论证BRAR相比固定随机化是否对各评价指标有明显提升，以提升其实际应用价值。

BRAR作为响应变量适应性随机化的一种具体实现，也需要考虑受试者特征的漂移(drift)，Karrison等[18]指出“任何响应变量适应性随机化的效果都会因受试者某些特征随时间产生系统性的变化而大打折扣”。针对受试者结局指标响应时间过长带来的漂移问题，协变量调整的响应变量适应性随机化(covariate adjusted response adaptive randomization,CARAR)能够进行较好处理，但是对于那些潜在的、不被知晓的或是不能被观测的混杂因素，CARAR仍有些无力。夏结来等[19]提出“响应变量适应性随机化对预后因素的均衡性、试验的检验效能、总一类错误、试验样本量等带来的影响不能忽略”，而本研究因不涉及具体每个受试者的数据而未评价其对组间预后因素均衡性的作用，需要在后续研究中进一步讨论。

鉴于BRAR在方案设计及具体实施时的复杂性，开发具备BRAR模拟预测评价功能、BRAR受试者入组分配功能的中央随机化系统十分必要，具体技术细节我们将在后续文章中予以报道。