超深层碳酸盐岩储层孔隙弹性动力学起裂规律

韦世明 夏阳 陈勉 卢运虎

1. 油气资源与探测国家重点实验室；2. 中国石油大学(北京)石油工程学院

0 引言

超深层碳酸盐岩地层埋深超过6 000 m，储层裂缝发育，钻进过程易发生漏失。为保证不发生地层流体侵入和井喷，故要求钻井液密度大于地层压力当量密度，并在钻井液中加入可酸溶暂堵剂，堵住漏失点。在堵漏剂承压能力足够的情况下，必须保证钻井液不会压裂地层。

以往对于井壁破裂压力的计算没有考虑到井眼周围应力场的时变特性，而且忽略了井筒与地层的流动耦合。井壁破裂模式主要可以分为H-W模式和H-F模式。Hubbert和Willis［1］在1957年通过三轴压缩实验总结出了H-W模式，Matthews和Kelly［2］在1967年提出的修正H-W模式，引入了骨架应力系数代替经验性的上覆压力系数，但骨架应力系数的使用需要大量的实际压裂资料，因此限制了此方法的应用。1969年，Eton［3］认为上覆压力梯度随井深变化，并将地层看作是平面应变问题求解，在H-W模式中引入了泊松比。Anderson［4］在1973年将Biot弹性多孔介质理论引入到井壁问题分析，使用有效应力系数修正孔隙压力的影响，同时，Anderson首次提出由测井资料计算破裂压力。Stephen［5］在1982年首次考虑构造应力对破裂压力的影响。以上均是在H-W模式的基础上进行修正，其最大的限制因素就是没有考虑岩石抗拉强度的影响。黄荣樽［6］在1984年提出了黄氏模型，模型中引入了两个水平方向的构造应力系数，并考虑了岩石抗拉强度的影响。黄氏模型与H-W模式形式上相同，因此可以归为H-W模式的一种。HW模式始终没有考虑渗流对破裂压力的影响，Haimson与Fairhurst［7］在1967年提出的H-F模式结合了有效应力与渗流的影响，认为井内流体压力的变化将引起井壁应力状态发生变化，当井壁应力超过岩石抗拉强度时发生破裂。

在钻井过程中，新地层被瞬间揭开后，井壁上的应力状态瞬间发生变化，由此引起的井壁载荷变化将以弹性波的形式向地层内部传递［8-10］；同时，井内流体也将与地层发生渗流作用。本文使用Biot孔隙弹性动力学理论，采用H-F模式，将地层中的渗流看作是不稳定渗流，研究了不同井底压力引起的井周应力场变化规律，以及井壁的破裂响应规律。

1 物理模型

图1是本文研究问题的物理模型，井眼形成后，在井壁上施加的载荷以弹性波的形式向地层内部传播，井壁上的载荷为井内液柱压力pw，在实际钻井过程中随时间发生变化。

图1 处于两向应力状态下的井眼—地层模型Fig. 1 Borehole-strata model in the state of two-dimension stress

考虑地层为平面应力状态，且两个水平主应力不相等，取水平主应力方向为x-y轴，最大水平主应力与最小水平主应力分别为 σH, σh，原始地层压力为p0。

2 数学模型

根据Biot孔隙弹性动力学理论［11］，假设井眼周围的介质为均质且各向同性的固体-流体的两相系统，则应力张量 σij和平均孔隙压力p为(本文采用拉为正、压为负的记法)

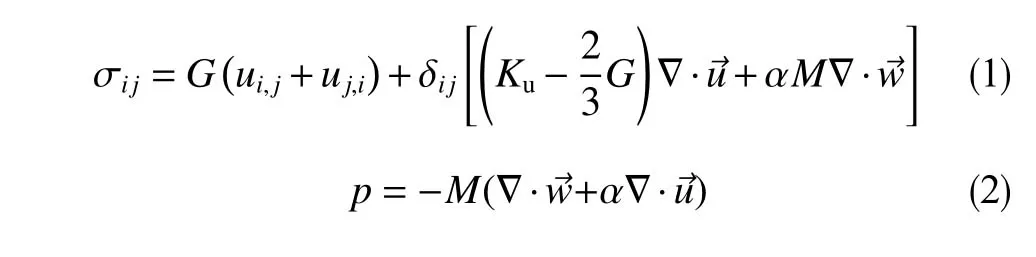
其中

式中，∇为梯度算子；G为岩石的剪切模量，MPa；ϕ为孔隙度；K、Ks、Kf分别为干岩石、岩石骨架颗粒和孔隙流体的体积模量，MPa；Ku为饱和流体的岩石体积模量，MPa；分别为岩石内部一点处的固体、流体的位移向量，m；δij为克罗内克符号，当i=j时，δij=1，否则δij=0；eij为应变分量；ui为固体位移分量，m；ui,j为位移导数，即ui,j=ui/xj，uj,i=uj/xi，xi与xj为坐标系；α为有效应力系数。

根据孔隙弹性动力学理论，孔隙流体流动的连续性可由耦合平衡方程表示。考虑孔隙流体的流动，Biot理论控制方程的位移形式为［12］

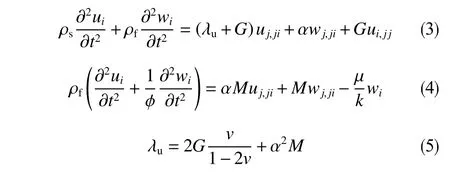
式中，ρs、ρf分别为岩石骨架的密度和孔隙流体的密度，kg/m3；v为岩石泊松比，k为岩石渗透率，μm2；μ为流体黏度，mPa· s 。

3 模型求解

图1所示问题直接求解较为困难，故将其分解为一种轴对称和一种非轴对称问题［13-15］，分别进行求解后再叠加，这在很多问题中都可以起到降低求解难度的目的。

3.1 问题分解

远场应力可分为两部分：两向相等应力作用的轴对称模式和不等应力作用的非轴对称模式。(0)模式为轴对称模式，(2)模式为非轴对称模式。对式(3)和式(4)进行拉普拉斯变换，消去时间项，之后根据Xia等的推导结果［16］，两种应力模式叠加问题的拉氏空间解为

求解式(3)、(4)可以得到两种模式中的解为

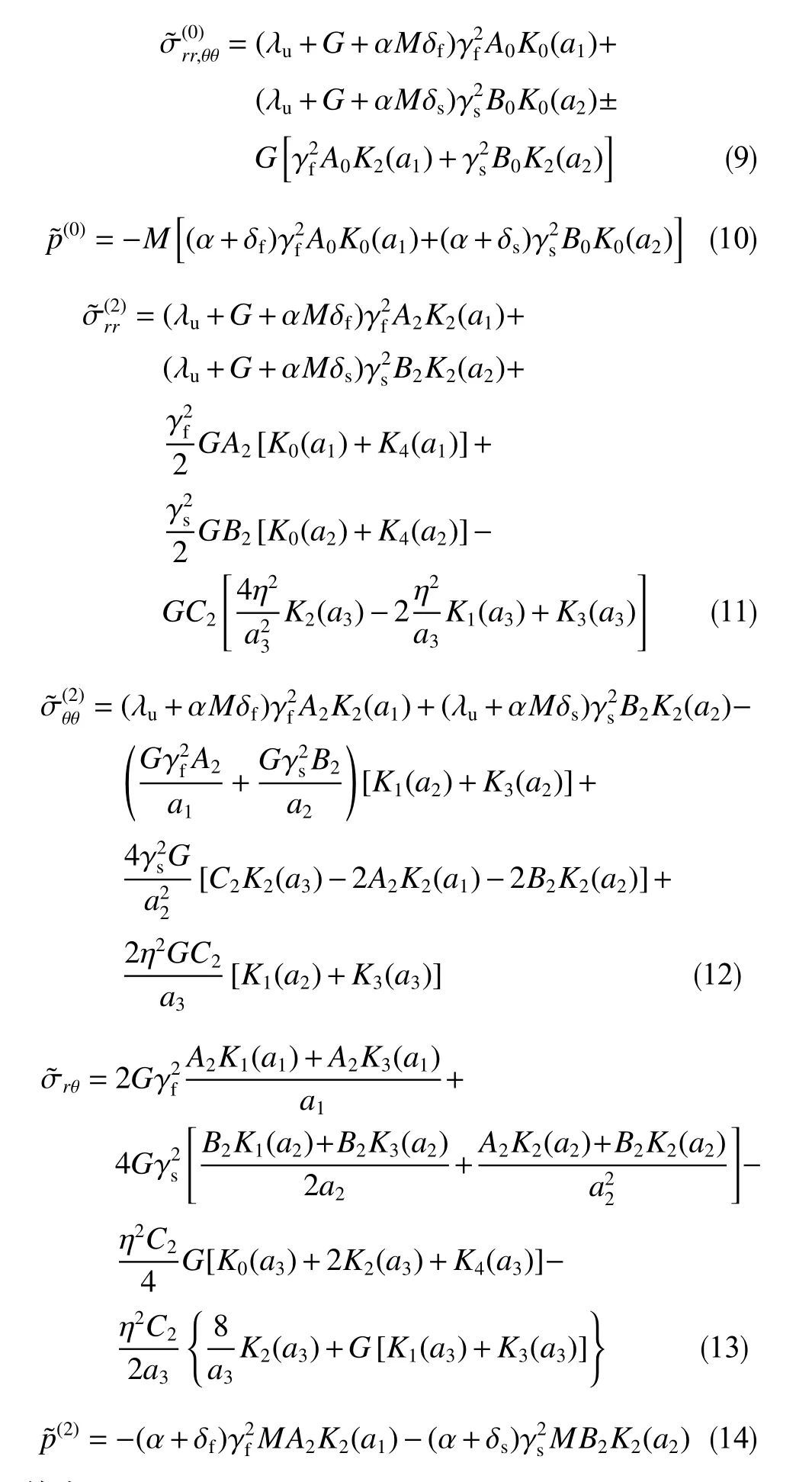
其中

式中，s为拉氏空间内的时间具有时间量纲，时间已被换成了无因次时间，当无因次时间为1时，对应的真实时间为2.87×10−5s。

将式(9)～(14)代入到式(6)～(8)即可得到图1所示问题的解。

3.2 初始和边界条件

在井眼被瞬间钻开的极短时间内，钻井液内的暂堵剂将对井壁进行封堵，在地层被压裂之前，钻井液在井眼与储层间保持缓慢渗滤，故可将内边界看作是定压边界。

在所建极坐标下，边界条件以增量形式，在拉氏空间表示为

初始条件为

式中，σrr、σθθ分别为径向、切向的正应力，MPa。

由以上边界条件和初始条件，使用Stehfest算法［17-18］进行反演即可得到真实时间域的应力场和孔隙压力场。

3.3 破坏准则

文中采取“拉为正、压为负”的记法，故随着井底压力和时间进行，地层中各点的第三主应力将最先变为正值。第三主应力可以写作［19］

取破坏函数为σFailure，当σFailure>0时地层起裂

式中，σ3为地层最小主应力，MPa；St为岩石抗拉强度，MPa。

4 结果及讨论

选取塔河油田的一口深井的地层参数，具体参数见表1。

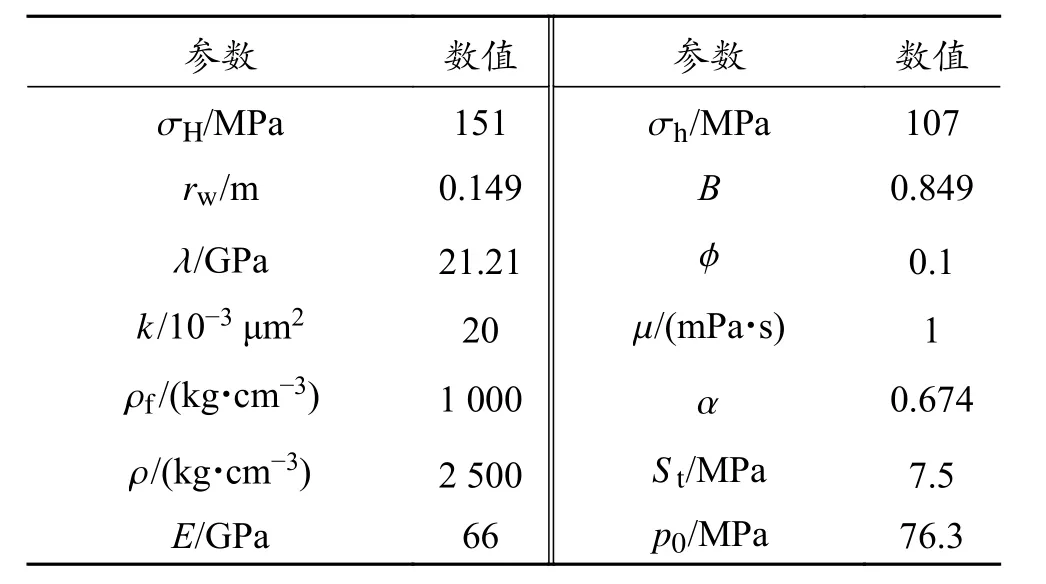
表1 所选地层的参数［20］Table 1 Parameters of the selected strata

4.1 井周应力场分布

选择井底压力90 MPa，研究近井周围地应力随时间变化规律。图2给出了不同时间下井周应力分布，井周应力均采用原始平均地应力进行了无因次处理。由图2可知，径向正应力最大值始终在0°方向最大，周向正应力在90°方向最小，切向应力在45°方向最大，这与弹塑性力学求解结果相同［21］。但是，随着时间的进行，井壁上的载荷变化向地层中传递，近井处的应力场变化明显。

4.2 不同井底压力对起裂的影响

选择不同的井底压力，研究它们引起的最大水平应力值在不同时刻的变化，选择最容易发生破裂的点，即最大主应力方向井壁处，得到图3。由图3可知，随着时间的进行，井壁处的破坏函数逐渐增大，当井底压力达到135 MPa时，井壁在t¯=105时起裂；当井底压力增大到150 MPa时，井壁的拉应力迅速增大，在t¯=64时即发生起裂。故增大井底压力，不仅可以使井壁起裂，当井底压力达到破裂压力后，继续增大井底压力将加速井壁起裂。

图2 不同时刻井周应力分布Fig. 2 Stress distribution around the well at different time

图3 危险点的破裂函数Fig. 3 The rupture function in the peril point

4.3 岩石弹性参数对起裂的影响

为了方便观察井壁破坏程度，将破坏函数进行二值化处理得到式（22），即破坏函数 σFailure大于0时令其为1，小于0时令其为0。

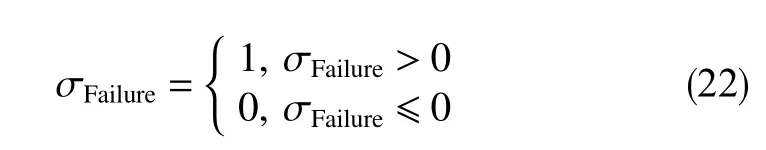
选取弹性模量和泊松比来表征各向同性均质地层的力学性质，图4、图5给出了井底压力150 MPa，无因次时间100（即2.87×10−3s时）不同弹性模量（22、33、44 GPa）和泊松比（0.21、0.26、0.31）情况下的井壁起裂情况。由图4可知，在选定时间点，井壁在原始最大水平主应力方向均发生破裂，且起裂规模很接近，故弹性模量的变化对井壁起裂产生影响很小。由图5可知，在选定的时间内，当泊松比为0.21时，井壁没有发生起裂；泊松比为0.31时，井壁发生起裂的范围明显大于泊松比为0.26的情况；由此可知，随着泊松比的增大，井壁起裂对井底压力的响应更加迅速，起裂的范围增大。

图4 弹性模量对井壁起裂的影响Fig. 4 The influence of elasticity modulus on fracture intiation

图5 泊松比对井壁起裂的影响Fig. 5 The influence of Poisson's ratio on fracture initiation

5 结论

(1)运用孔隙弹性动力学理论，研究了碳酸盐岩储层在钻进过程中的瞬态拉伸破坏响应。在储层被钻开的瞬间，井壁上受到的载荷变化以压力波的形式向地层内传播，引起井眼周围的地应力和孔隙压力发生明显变化。

(2)选择塔河一口井为算例，在钻开井眼的瞬间，井壁上所受到的最大拉应力尚不至于引起井壁拉伸破坏，但是在很短时间内，随着时间进行，井壁上的最大拉应力迅速增大，当井内压力达到135 MPa时，井壁在t¯=150，即经过4.3×10−3s起裂。

(3)井底压力越高、地层泊松比越大，井壁的起裂响应越迅速。考虑到所选井的垂深为6 980 m，以及钻井液在循环过程中的摩阻，由此给出塔河深部碳酸盐岩油藏在储层钻进时，最大安全钻井液的密度不能超过1.93 g/cm3。如果继续增大井底压力，则地层迅速起裂。