超硬灰岩地层侧钻分支水平井侧钻效率与重入评价
2020-06-18罗远儒陈勉
罗远儒 陈勉
1. 中国石油长城钻探工程有限公司;2. 中国石油大学(北京)石油天然气工程学院
采用分支水平井能有效提高致密油气产量[1],但在钻井过程中存在诸多挑战[2]。在辽河油田进行分支水平井侧钻施工时,部分分支侧钻点位于潜山地层的硬质灰岩层中,由于该地层岩石的硬度大(其抗压强度最高可达150 MPa)、研磨性强,可钻性非常差,在该处进行侧钻时,采用传统的悬空侧钻施工难度很大,需要在施工工艺上进行改进,以提高侧钻成功率及侧钻效率。目前在现场采取先钻较小尺寸的分支井,再钻主井眼的复合井眼侧钻技术来解决这个难题。然而,目前这项技术仍不成熟,主要体现在施工中以经验性的技术措施为主,缺乏理论建模,现场人员技术水平参差不齐,造成侧钻效率没有达到最优。针对该情况,笔者在侧钻效率的计算及影响因素、侧钻钻具组合优选等方面进行了深入研究。此外,当需要起下钻时还必须保证钻具能够顺利地进入主井眼,因此下钻重入主井眼是侧钻分支水平井不可回避的另一个难题。笔者通过分析钻具重入难度的影响因素和重入评价来指导分支水平井水平段轨道优化,为现场施工提供参考。
1 侧钻效率计算模型
在复合井眼侧钻施工时,一般先钻出一个尺寸比主井眼小的分支井眼,完钻后需要起钻换大尺寸的钻头,再钻主井眼。这里把主井眼称作“侧钻井”。主井眼钻进一段时间后与分支井眼就会出现夹壁墙(图1),当夹壁墙的厚度Ha达到一定程度后,就不会被钻具的运动破坏,此时认为“侧钻”成功[3]。这里定义一个地层侧钻效率的概念:即在一定的钻具组合条件下,从侧钻点开始,到侧钻井眼与分支井眼间的夹壁墙厚度达到Ha所用的纯钻进时间,这个时间越短则钻具的侧钻效率越高。
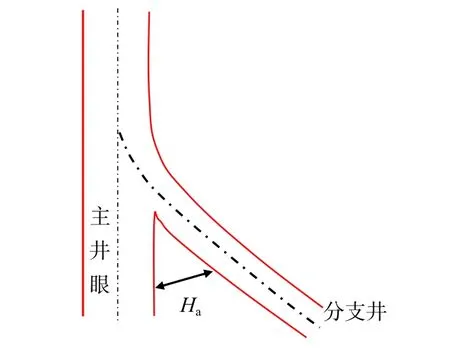
图1 夹壁墙厚度示意图Fig. 1 Schematic thickness of multilateral well junction
1.1 分支井井眼轨迹计算
求取Ha的大小,首先必须知道距离“侧钻井深”最近的上部测点以及已钻分支井“侧钻井深”以下的下一个测点的测斜数据。现有测斜方法大约有20余种,其中斜面圆弧法、圆柱螺线法和自然曲线法是3种较为推荐的方法[4]。分支井钻进时一般采用动力钻具进行滑动钻进,钻出的井眼轨迹近似于空间斜平面上的曲线,因此通常采用斜面圆弧法进行计算,且采用斜面圆弧内插给定插入点井深来计算相对更精确[5],内插计算点的间隔建议以0.5 m为一个计算点。具体计算公式如下。

式中,La为上测点井深,m;Li为插入点井深,m;ΔLi为插入点井深相对上测点增量,m;γ为全角变化率,(°)/30 m; ∆γi为插入点全角变化率增量,(°)/30 m;αa为上测点井斜角,°;αi为插入点井斜角,°; φa为上测点方位角,°;φi为插入点方位角,°;Da、Na、Ea为上测点的井口坐标值,m;Di、Ni、Ei为插入点的井口坐标值,m。
1.2 主井眼轨迹计算
通过钻具组合受力分析,可以得到工具的侧向力以及钻头转角。首先利用平衡曲率法计算工具造斜率,把这个造斜率作为待钻轨道的井眼曲率,钻头在侧钻以后沿此井眼曲率进行钻进,而钻进的方向,认为是钻头轴线所指方向。在进行井眼轨迹预测时,需要考虑钻头和地层的各向异性的影响[6-7]。Ho在前人研究的基础上提出了一种三维钻头与地层相互作用的通用模型[8],该模型可以很好地解释地层和钻头的各向异性特征,可用于定向井(或深竖井)井眼轨迹预测。图2为Ho提出的钻头与地层相互作用模型各坐标系方向规定示意图,Ef为钻头作用力合力方向的单位矢量,Ea为钻头的轴线方向的单位矢量,Ed为待钻地层的法线方向的单位矢量,这样就可以用Ef、Ea、Ed来表示钻头钻进的方向,Er即为最终钻头前进方向的单位矢量。对于井眼前进方向的具体表达式为

图2 Ho钻头与地层相互作用模型示意图Fig. 2 Schematic model of the interaction between Ho bit and strata
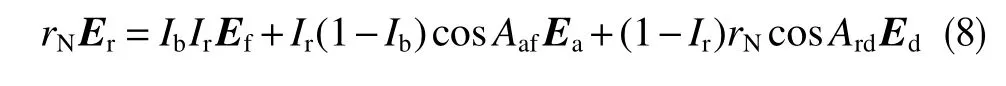
式中,rN为钻头对各向同性地层的钻进效率;Aaf为钻头受到的合力方向与钻头轴线的夹角,°;Ard为地层法线方向与钻头钻进方向的夹角,°;Ib为钻头各向异性指数,为钻头侧向钻进效率与轴向钻进效率之比,可通过室内实验得到;Ir为地层各向异性指数,为沿地层层面方向的钻进效率与沿地层法向的钻进效率之比,可通过室内实验或资料反算得到。
为了计算方便,在石油工程领域通常将岩石简化为各向同性材料[9]或横观各向同性材料。考虑到超硬灰岩地层岩石坚硬,不像页岩地层层理发育、各向异性强,因此在进行计算时忽略其各向异性,Ir的值取1,将计算公式简化为

在式(9)中,Ef、Ea可以通过底部钻具组合力学分析模型计算得到,这样,方程中只有3个独立变量,即rN和Er(相当于2个独立变量,井眼前进方向的井斜角α1和方位角 φ1)。由于式(9)为矢量方程,相当于3个标量方程,3个方程3个未知数,故该方程是可以求解的。
假设通过底部钻具组合力学分析模型计算得到的钻头作用力合力方向井斜角和方位角分别为αf和φf、钻头轴线方向的井斜角和方位角分别为αa和φa,则式(9)可展开为

其中
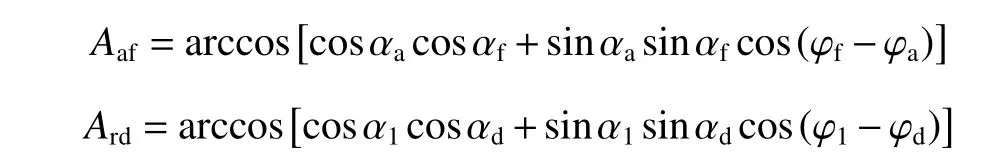
显然,方程组(10)中只有rN、α1和 φ1等3个独立变量,通过求解该非线性方程组,可以求出α1和φ1。对于底部钻具组合受力分析模型,利用纵横弯曲梁理论进行计算,鉴于其理论模型应用已经比较成熟,这里不再给出其理论推导过程。
依据实际情况确定出合理的造斜率区间,在此区间内,每一个曲率都对应着一个侧向力,通过搜索法找出侧向力的最小值,此时所对应的曲率即为平衡曲率。这样,求出α1和 φ1后,就可以通过平衡曲率法求出工具的造斜率,再加上施工时底部钻具组合受力计算求出的钻头转角,就可以确定待钻轨道的轨迹数据。
1.3 侧钻效率求解
求出待钻井眼的轨迹后,同样可以通过插值的方法求出侧钻点以下的各数据点,从而可以通过式(11)求得夹壁墙Hai的值。
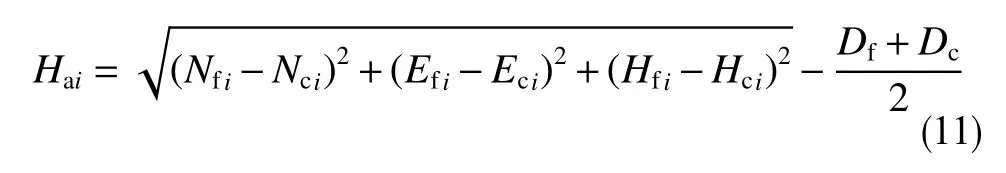
式中,Hai为夹壁墙厚度,m;Nfi、Efi、Hfi为分支井内插点的坐标位置,m;ci、Eci、Hci为侧钻主井眼内插点的坐标位置,m;Df为分支井直径,m;Dc为侧钻主井眼直径,m。
根据式(11)可以得出两个井眼轨迹相同井深处夹壁墙的厚度,当Hai≥Ha时,认为侧钻成功,此时的井深记为Hma,若侧钻点的井深为Hca,就可以得到侧钻效率Se,其值越小,侧钻效率越高。

式中,Vj为侧钻时机械钻速,m/h。
对于侧向力正、负的规定,由于目的是为了侧钻主井眼,这里规定有利于形成主井眼的侧向力为正。如:把工具面调向低边方向,形成的侧向力为一个降斜力,但这里不以增、降斜来判断侧向力的正、负,而是认为只要侧向力是有利于主井眼的形成,其为正值。以现场给定底部钻具组合为例:Ø215.9 mm钻头+ Ø172 mm×1.0°螺杆+212球扶+ Ø127 mm加重钻杆3根+ Ø127 mm钻杆+ Ø127 mm加重钻杆50根+钻杆。该钻具组合的造斜率在10.2 (°)/30 m左右,得到钻具造斜率后,分析该钻具组合在不同钻压、装置角条件下侧钻效率的大小。
首先把装置角调整到0°,计算钻头侧向力以及侧钻效率Se随钻压的变化。进行悬空侧钻时,不能施加钻压,Se较大,侧钻效率较低。由图3可看出,随着钻压的增加,钻头的侧向力明显增加,Se的值减小,侧钻效率增加。但是,随侧向力增加,侧钻效率并非线性增加,当钻压达到一定程度后,侧钻效率增加并不明显。对于图中描述的情况,可以看出在该钻具组合及装置角条件下,钻压在40~80 kN的范围内比较合理。

图3 钻头侧向力和侧钻效率随钻压的变化Fig. 3 Variation of bit side force and sidetracking efficiency with weight on bit (WOB)
2 侧钻分支水平井重入评价
对于超硬地层分支水平井施工,一般采用从近至远的施工顺序,先钻出水平井段的主井眼,然后钻出第一个分支井,再沿主井眼钻进,进而钻下一个分支井段(如图4所示)。然而,由于前面的分支井已经钻完,如何保证钻具或套管在重入过程中进入主井眼而不是进入分支段成了一个难题。对此,提出了一个管柱下入难度系数的概念,通过计算施工时给出的管柱下入难度系数的大小,来判断管柱是否能够重入主井眼,保证现场施工的顺利进行。
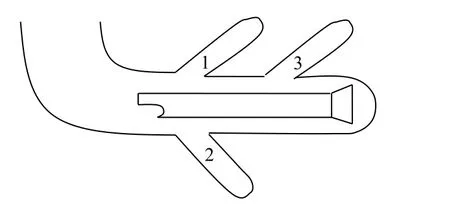
图4 分支水平井钻具的重入过程Fig. 4 Reentry process of drilling tool in branch horizontal well
2.1 重入难度系数计算方法
重入难度系数定义:在分支水平井“侧钻点”位置井深处,钻具在井眼中旋转一周,底部管柱中心轴线向井深延伸方向落在“侧钻”主井眼中的概率。对于底部钻具组合,即为钻头轴线指向井深延伸方向,对于套管柱,为套管鞋中心轴线方向。
要计算钻柱的重入难度系数,首先必须知道管柱在井眼中的形状,求得钻头处的转角大小,根据底部钻具组合受力分析模型[10],在求出钻头处侧向力的同时,也求得了转角的大小。这样,可以把钻具在井底按照固定的角度旋转,求出每次旋转后钻头轴线在侧钻成功后井底平面上的落点,进而求出其落在主井眼中的概率,即为所求的重入难度系数。
如图5所示,侧钻点的井深为Hca,侧钻成功后(即形成一定厚度的夹壁墙)的井深为Hma,水平段侧钻进尺ΔHc=Hma−Hca。钻头处轴线与水平段主井眼的轴线的夹角为θ,则可以求出钻头轴线所指方向在侧钻成功井深处井底平面上的落点与井眼轴线的距离ΔDc,若落点的位置在井眼轴线的下方,则令ΔDc为0,这样就可以判断落点是否在主井眼中。

图5 侧钻井底平面图Fig. 5 Plane view of sidetracking bottom hole
对于难度下入系数Pn,可用下式计算

式中,Pn为难度下入系数;ηi为常数,当ΔDc≤Dc/2时,ηi=1;当ΔDc>Dc/2时,ηi=0;n为管柱在井底旋转一周的次数。
2.2 重入难度的影响因素分析
分支水平井管柱能否重入主井眼的影响因素有多个方面。针对水平主井眼,由于在钻分支井与主井眼时采用了高、低边分离技术。一般情况下,在重力作用下套管柱管壁与井眼下壁接触,套管柱端部中心位置处于井眼轴线位置以下,且水平段井眼曲率很小,端部转角与井眼轴线的夹角一般非常小,Pn的值近似为1,因此,认为此时套管柱可以顺利下入主井眼[11]。受井眼轨迹、底部钻具组合以及装置角变化的影响,钻柱能否进入主井眼,需要通过计算Pn来判断其是否能够重入。若Pn偏小,可以调整底部钻具组合或者调整装置角的大小来提前预防钻具进入分支井。针对钻具组合以及井眼轨迹形状,先通过底部钻具组合受力分析模型计算出钻压为0时不同装置角条件下的钻头转角,这里同样设置每次装置角转动10°,水平段侧钻进尺ΔHc取5 m,计算的钻头转角及ΔDc的值如图6所示。从而,通过ΔDc值与井眼半径的大小来判断钻具是否能够进入主井眼(即ΔDc为0,这样就可以判断落点是否在主井眼中)。对于图6所示的结果可以求出Pn的值为0.806。
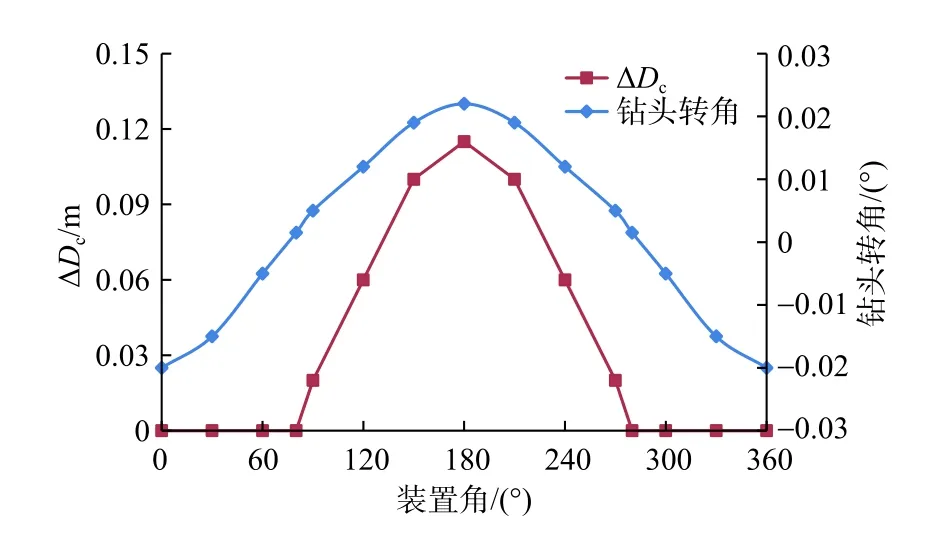
图6 ΔDc值与钻头转角随装置角变化Fig. 6 Variation of ΔDc and bit rotation angle with tool face angle
辽河油田多口井的试验结果表明,应用复合井眼技术,一般情况下可以将侧钻时间由原来的120~150 h降低到7~12 h,使得侧钻效率提高了10倍以上。例如静52-H1Z井,通过应用复合井眼技术,钻井周期比设计减少了近100 h。
3 结论
(1)通过侧钻分支水平井侧钻效率与重入评价研究,采用复合井眼侧钻技术可以有效解决潜山超硬灰岩地层水平井段窗口设计窄、轨迹精度要求高和控制难度大的问题。
(2)现场试验表明,复合井眼侧钻技术可使侧钻时间降低90%以上,同时侧钻效率提高10倍以上。
(3)为使侧钻效率更优,今后还需要在结合岩石力学理论建模和提高现场人员技术水平方面做进一步研究和努力。
